Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Probabilidade Condicional

Ver Todos os Exercícios

Teoria

Faaala Aííí!!! Belezinha??

Imagine a seguinte situação:

Carlos tirou uma carta do baralho, sabendo que a carta é de copas, qual a probabilidade de ser uma dama ?

Nesse caso, para calcular a probabilidade precisamos prestar atenção que acontecem duas coisas distintas:

A :   a   c a r t a   s e r   d e   c o p a s

B :   a   c a r t a   s e r   a   d a m a   d e   c o p a s .

Percebe que nesse caso um evento depende do outro? A probabilidade desta carta ser uma dama de copas depende o evento anterior, pois a carta inicialmente tem que ser de copas .

Quando temos esse tipo de situação, calcular a probabilidade de um evento acontecer sabendo que um outro evento já aconteceu, chamamos isso de PROBABILIDADE CONDICIONAL.

Genericamente podemos ter duas situações:

P A / B → p r o b a b i l i d a d e   d e   A ,   d a d o   B

P B / A → p r o b a b i l i d a d e   d e   B ,   d a d o   A

Tudo bem... mas como calcular isso?

Vamos lá! Para chegarmos na fórmula vamos tentar resolver o exemplo:

Carlos tirou uma carta do baralho, sabendo que a carta é de copas, qual a probabilidade de ser uma dama ?

No final do processo, Carlo quer que a carta do baralho escolhida seja uma dama de copas, certo? Para isso acontecer é preciso duas coisas:

  1. A carta ser de copas ( P A )
  2. A carta ser uma dama de copas ( P B / A )

Na matemática quando queremos que duas coisas aconteçam usamos o “e” certo? Queremos que a carta seja de copas e uma dama! Ou seja, para calcular a probabilidade dos dois eventos acontecerem, basta calcular a probabilidade da interseção desses eventos:

P ( A ∩ B ) = P ( A ) . P ( B / A )

Mas isso é a probabilidade dos dois eventos acontecerem, concorda?! Se quisermos calcular apenas a probabilidade da carta ser uma dama visto que ela é de copas P ( B / A ) podemos apenas isolar essa expressão:

P ( A ∩ B ) = P ( A ) . P ( B / A )

P B / A = P ( A ∩ B ) P ( A )

Prontinho já temos a fórmula, bora voltar para o exemplo?

Primeiro precisamos calcular a P ( A ∩ B ) , que nesse caso é a carta escolhida ser uma dama de copas. Como temos 52 cartas no baralho e apenas 1 dama de copas:

P A ∩ B = 1 52

Para calcularmos P A podemos considerar que A é o novo espaço amostral, que chamaremos de espaço amostral reduzido.

Antes, o Ω eram todas cartas do baralho, mas depois de sabermos de A , o Ω se reduziu a apenas às cartas de copas que são: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, valete, dama, rei, ou seja, temos 13 opções!

Agora basta considerar no numerador apenas o número de elemento de B que satisfazem A , a interseção. Beleza?!

Teremos que:

P A = 13 52 = 1 4

Só resta agora descobrir o valor de P ( B / A ) :

P B / A = 1 52 1 4 = 4 52 = 1 13

A probabilidade da carta ser uma dama visto que a carta e de copas é de 1 13 . Show de bola?!

Vamos trabalhar agora com exemplos que vão facilitar as coisas pra você.

Exemplo1

Imagine que temos um saco com 2 bolas laranjas e 3 vermelhas. Qual seria a probabilidade de retirarmos 2 bolas vermelhas em sequência?

Vamos lá! Temos os seguintes eventos possíveis:

A :   p r i m e i r a   b o l a   s e r   v e r m e l h a

B :   p r i m e i r a   b o l a   s e r   l a r a n j a

C :   s e g u n d a   b o l a   s e r   v e r m e l h a

D :   s e g u n d a   b o l a   s e r   l a r a n j a

Vamos primeiro organizar quais são os eventos que queremos :

A :   p r i m e i r a   b o l a   s e r   v e r m e l h a

C :   s e g u n d a   b o l a   s e r   v e r m e l h a

Queremos calcular a prababilidade de retirarmos a segunda bola vermelha dado que a primeira bola retirada também foi vermelha. Vamos denotar isso por P ( C / A ) , beleza?!

Assim, para calcular P ( C / A ) precisamos primeiro da probabilidade P A .   Se temos 5 bolas totais e três vermelhas temos que a probabilidade de sair primeiro uma bola vermelha é:

P A = 3 5

Agora vamos calcular P ( A ∩ C ) . Note que queremos que a segunda bola retirada for vermelha, como a primeira bolinha foi retirada, restam 4 bolas no total e 2 bolas vermelhas então a probabilidade da segunda bolinha for vermelha é 2 4 . Desse modo:

P A ∩ C = 3 5 × 2 4 = 6 20 = 3 10

Agora podemos calcular P ( C / A ) :

P C / A   = P ( A ∩ C ) P ( A ) = 3 10 ∙ 5 3 = 1 2

Se calcularmos todas as probabilidades condicionais possíveis desse exemplo podemos montar uma árvore de probabilidades, que será muito útil para resolver várias situações:

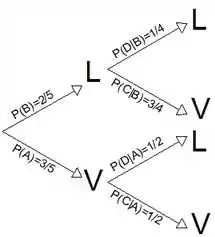
Se em uma questão for necessário calcular as probabilidades de interseção podemos usar essa árvore de possibilidades para organizar nossos dados. Por exemplo:

Qual a probabilidade de sair primeiro uma bolinha laranja e depois uma vermelha? Olhando para a árvore temos que:

P B ∩ C = P B . P C / B = 2 5 ∙ 3 4

Legal né? Vamos fazer mais exercícios?

Exemplo1

Exercícios Resolvidos

Exercício Resolvido #1

Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006,124-40

A empresa M&B tem 15.800 empregados, classificados de acordo com a tabela abaixo.

Se um empregado é selecionado ao acaso, calcular a probabilidade de ser uma mulher, dado que é um empregado com menos de 25 anos.

Passo 1

O enunciado dá uma tabela cheia de número (=dados) e pede: a probabilidade de ao selecionar um empregado ao acaso ela ser mulher, SABENDO que é um empregado com menos de 25 anos.

Percebe que temos uma probabilidade condicional pois sabemos que um empregado tem menos de 25 anos, beleza?!

Podemos utilizar a fórmula então da probabilidade condicional:

P F A = P F ∩ A P A

Mas quem é F e quem é A ?

Passo 2

Vamos considerar

F : o   e m p r e g a d o   s e r   m u l h e r

A : o   e m p r e g a d o   t e r   m e n o s   d e   25   a n o s

Então queremos calcular P F A   → P r o b a b i l i d a d e   d e   F ,   d a d o   A .

Ou seja, probabilidade do empregado ser mulher, dado que é um empregado com menos de 25 anos.

Passo 3

Vamos olhar pra essa tabela?

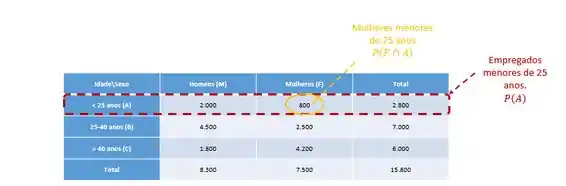
Temos então que

P F ∩ A = 800

Que é a quantidade de empregadas com menos de 25 anos.

da mesma forma,

P A = 2800

Que é a quantidade de empregados com menos de 25 anos.

Beleza?!

Assim,

P F A = P F ∩ A P A = 800 2800 ≅ 0,29

Resposta

0,29

Exercício Resolvido #2

Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006,115-18

Um dado é viciado, de tal forma que a probabilidade de sair um certo ponto é proporcional ao seu valor (por exemplo, o ponto 6 é três vezes mais provável de sair do que o ponto 2). Calcular:

a) a probabilidade de sair 5, sabendo-se que o ponto que saiu é ímpar;

b) a probabilidade de tirar um número par, sabendo-se que saiu um número maior que 3.

Passo 1

Primeira coisa: Interpretar o enunciado e escrever as informações retiradas dele

Estamos falando de um dado, portanto Ω = { 1,2 , 3,4 , 5,6 }

O enunciado diz: a probabilidade de sair um certo ponto é proporcional ao seu valor

Então imagine que a probabilidade de sair 1 é n:

P 1 = n

A probabilidade de sair 2 é duas vezes maior:

s e   P 1 = n     e n t ã o     P 2 = 2 n

Podemos calcular todas as probabilidades em função de n :

P 1 = n → P 3 = 3 n

P 1 = n → P 4 = 4 n

P 1 = n → P 5 = 5 n

P 1 = n → P 6 = 6 n

Mas qual o valor de n?

Sabendo que a soma de todas as probabilidades deve ser igual a 1, faremos:

P 1 + P 2 + P 3 + P 4 + P 5 + P 6 = 1

n + 2 n + 3 n + 4 n + 5 n + 6 n = 21 n = 1

n = 1 21

Passo 2

a) a probabilidade de sair 5, sabendo-se que o ponto que saiu é ímpar;

Seja

- “5”: Evento de sair o número 5

- A : Evento sair ímpar

Queremos: P ( 5 | A )

Estamos falando de probabilidade condicional certo? Então vamos para a fórmula!

P C = P B ∩ C P C

Substituindo teremos

P A = P 5 ∩ A P ( A )

Então precisamos calcular essas duas probabilidade né? Vamos lá!

- P 5 ∩ A : Probabilidade de ser 5 e ímpar

Bom, sempre que temos o número 5 ele é ímpar né? Então falaremos que:

P 5 ∩ A = P 5 = 5 n = 5 21

- P A : Probabilidade de ser ímpar

Temos que

A = 1,3 , 5

P A = P 1 + P 3 + P 5 = n + 3 n + 5 n = 9 n = 9 21

Assim

P A = P 5 ∩ A P ( A ) = 5 21 9 21 = 5 9 = 0,56

Passo 3

- b) ) a probabilidade de tirar um número par, sabendo-se que saiu um número maior que 3.

Novamente probabilidade condicional certo? Agora com os eventos:

- B: Evento retirar um número par

- D: Evento retirar números maiores que 3.

Queremos P B , que será:

P B = P B ∩ D P D

Agora é só calcular essas probabilidades né?

- P B ∩ D :   Probabilidade de retirar um número par MAIOR do que 3.

Se fosse maior que três temos 3 possibilidades(4,5,6) porém como ele quer um número maior que 3 e par temos que:

B ∩ D = 4,6

P B ∩ D = P 4 + P 6 = 4 n + 6 n = 10 n = 10 21

- P(D): Probabilidade de retirar um número maior do que 3

D = 4,5 , 6

P D = P 4 + P 5 + P 6 = 4 n + 5 n + 6 n = 15 n = 15 21

Entãão teremos:

P B = 10 21 15 21 = 10 15 = 2 3 = 0,67

Resposta

a) 0,56

b)0,67

Exercício Resolvido #3

UFRJ, ProbEst, P1/2013.1, 1

Para sagrar-se campeão de um torneio de tênis, um jogador precisa vencer quatro partidas sucessivas, todas elas eliminatórias. José é um dos participantes e suas probabilidades de vitória em cada partida (caso ele não tenha sido eliminado até então) foram estimadas em: 80% na 1ª partida, 70% na 2ª partida, 60% na 3ª partida (semifinal) e 50% na 4ª partida (final). Observe que estas probabilidades independem de quem seja o seu adversário em cada partida. Calcule as probabilidades de que José:

(a) Não consiga chegar até a final.

(b) Consiga chegar a uma semifinal, dado que não será o campeão.

Passo 1

Primeiramente vamos montar o espaço amostral desse torneio de tênis.

Quais os resultados possíveis ?

e 1 :   eliminação na primeira partida

e 2 :   eliminação na segunda partida

e 3 :  eliminação na semifinal

e 4 :  eliminação na final

v :  vencer o torneio

Então:

Ω → e 1 , e 2 , e 3 , e 4 , v

Passo 2

Agora vamos determinar a probabilidade de cada resultado desse.

Probabilidade de ele perder de primeira é 1 menos a prob. de ele ganhar a primeira partida.

p e 1 = 1 - 0,80 = 0,2

Prob. de ele perder na segunda é igual a prob. de ele ganhar a primeira vezes a prob. de ele perder a segunda.

p e 2 = 0,8 × 1 - 0,7 = 0,24

Prob. de ele perder na terceira é a prob. de ele ganhar a primeira vezes a prob. de ganhar a segunda vezes a prob. de perder a terceira.

p e 3 = 0,8 × 0,7 × 1 - 0,6 = 0,224

Prob. de ele perder na quarta segue o mesmo raciocínio.

p e 4 = 0,8 × 0,7 × 0,6 × 1 - 0,5 = 0,168

E a prob. de vencer o torneio é:

p v = 0,8 × 0,7 × 0,6 × 0,5 = 0,168

Assim, a probabilidade dele não chegar até a final é

p e 1 + p e 2 + p e 3 = 0,2 + 0,24 + 0,224 = 0,664

Passo 3

(b)

Chamando de:

S :  chegar a semifinal

C :  ser campeão

O exercício agora pede P S     C c ) . Probabilidade de chegar a semifinal, dado que não foi campeão.

Pela fórmula da probabilidade condicional:

P S C c = P S ∩ C c P ( C c )

Passo 4

A gente sabe que:

C → v

Único caso em que José é campeão.

P C = p v = 0,168

Com isso:

P C c = 1 - P C

P C c = 0,832

No mesmo raciocínio.

S ∩ C c → e 3 , e 4

Porque nesses dois casos José chega pelo menos a semifinal, mas não é campeão.

P S ∩ C c = p e 3 + p e 4

      = 0,392

Passo 5

Agora é substituir na fórmula.

P S C c = 0,392 0,832

P S C c ≈ 0,471

Resposta

a 0,664

b   0,471

Exercício Resolvido #4

Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006,123-34

Um empreiteiro apresentou orçamentos separados para a execução da parte elétrica e da parte de encanamento de um edifício. Ele acha que a probabilidade de ganhar a concorrência da parte elétrica é de ½. Caso ele ganhe a parte elétrica, a chance de ganhar a parte de encanamento é de ¾ ; caso contrário, essa probabilidade é de 1/3. Qual a probabilidade de ele:

a) ganhar os dois contratos?

b) ganhar apenas um?

c) não ganhar nada?

Passo 1

Eeepa! Muuuita informação certo? Muita confusão então. Vamos tentar escrever o enunciado através de um diagrama?

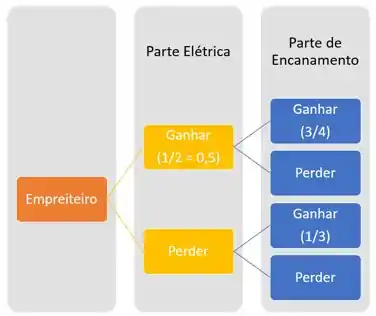
Passo 2

Agora vamos completar esse diagrama?

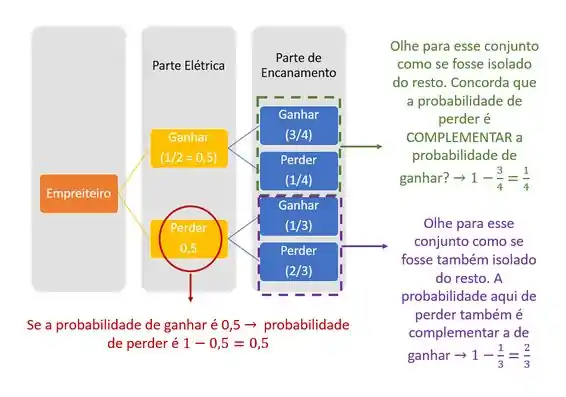
Passo 3

Agora temos a probabilidade de cada etapa. Mas pera aí, você sabe o que cada parte significa?

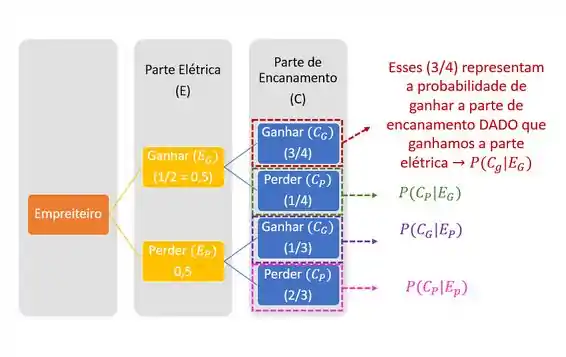
Passo 4

Agora que já entendemos direitinho o diagrama vamos olhar para o que ele pede:

a) Probabilidade de ganhar os dois contratos

O que ele pede é: P ( E G ∩ C G )

Bom, nós sabemos que

P E G = 0,5

P C G E G = 3 4

Lembrando da fórmula da condicional teremos:

P C G E G = P E G ∩ C G P E G →     P E G ∩ C G = P C G E G . P E G

Substituindo

P E G ∩ C G = 3 4 . 1 2 = 3 8 = 0,375

Passo 5

b)Probabilidade de ganhar apenas um?

Bom, ganhar apenas um significa:

i- Ganhar a parte elétrica e perder a parte do encanamento

ii- Perder a parte elétrica e ganhar a parte do encanamento

Vamos calcular a probabilidade de cada um e somar ok?

Passo 6

i) Ganhar a parte elétrica e perder a parte do encanamento → P ( E G ∩ C P )

Vamos usar a mesma ideia da letra (a)!

Sabemos

P E G = 0,5

P C P E G = 1 4

Pela fórmula da probabilidade condicional temos

P C P E G = P E G ∩ C P P E G → �� P E G ∩ C P = P C P E G . P E G

P E G ∩ C P = 1 4 . 1 2 = 1 8

Passo 7

ii) Perder a parte elétrica e ganhar a parte do encanamento → P ( E P ∩ C G )

Sabendo que

P E P = 0,5

P C g E P = 1 3

Utilizando a fórmula de probabilidade condicional....

P C g E P = P E P ∩ C G P E P →   P E P ∩ C G =   P C g E P . P ( E p )

P E P ∩ C G = 1 3 . 1 2 = 1 6

Passo 8

Somando (i) e (ii):

1 8 + 1 6 = 7 24 ≅ 0,292

Passo 9

c) Probabilidade de não ganhar nada? →   Não ganhar a parte elétrica E não ganhar a parte de encanamento → P ( E P ∩ C P )

Sabemos que

P E P = 0,5

P C P E P = 2 3

Usando de novo a fórmula da probabilidade condicional

P C P E P = P E P ∩ C P P E P →   P E P ∩ C P =   P C P E P . P ( E p )

P E P ∩ C P = 2 3 . 1 2 = 1 3 ≅ 0,333

Resposta

a) 0,375

b)   ≅ 0,292

c) ≅ 0,333

Exercício Resolvido #5

Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006,

60. Como fica a relação abaixo para n eventos quaisquer A 1 , A 2 , A 3 … A n ?

P A ∩ B ∩ C = P A . P B | A P ( C | A ∩ B )

Passo 1

Primeira coisa: Não pira!

O enunciado pede a relação para n eventos quaisquer, mas vamos olhar primeiro essa relação? Tá, vamos lá...

Essa relação é verdadeira? Bom, pelo enunciado parece que sim, mas vamos entender ela.

P A ∩ B ∩ C = P A . P B | A P ( C | A ∩ B )

Vamos olhar para o lado direito primeiro e ver como podemos “abrir” essa equação. Podemos começar aplicando a fórmula de probabilidade condicional com P B / A :

P B | A = P A ∩ B P A

Também podemos abrir o P ( C | A ∩ B ) , com a mesma fórmula de probabilidade condicional:

P C | A ∩ B = P A ∩ B ∩ C P A ∩ B

Então, vamos substituir esses valores na equação que temos e ver o que encontramos:

P A ∩ B ∩ C = P A . P B | A P ( C | A ∩ B )

P A ∩ B ∩ C = P A . P A ∩ B P A       P A ∩ B ∩ C P A ∩ B

Corta bastante coisa né?

Cancelando cada lado teremos que:

P A ∩ B ∩ C = P A ∩ B ∩ C

Ok, sabemos que essa relação é coerente!

Passo 2

Agora que entendemos melhor o mecanismo, vamos olhar para o caso com quatro eventos... A ideia de olhar para quatro é ver o que muda e como muda para conseguir fazer uma analogia com o caso com n eventos ok? Vamos fazer o caminho inverso agora:

P A ∩ B ∩ C ∩ D = P A ∩ B ∩ C ∩ D

Bom, podemos isolar o lado esquerdo:

P A ∩ B ∩ C ∩ D = P ( A ∩ B ∩ C ∩ D )

Agora vamos aplicar a fórmula da probabilidade condicional:

P X | Y = P X ∩ Y P Y → P X ∩ Y = P X | Y . P Y

Então

P A ∩ B ∩ C ∩ D = P D | A ∩ B ∩ C . P ( A ∩ B ∩ C )

Substituindo P ( A ∩ B ∩ C ) :

P A ∩ B ∩ C ∩ D = P D | A ∩ B ∩ C P B | A . P A P ( C | A ∩ B )

Reorganizando

P A ∩ B ∩ C ∩ D = P A . P B | A P C | A ∩ B . P D | A ∩ B ∩ C

Notamos então que ao fazermos para quatro eventos, acrescentamos uma parcela. E essa parcela é algo do tipo:

P ( A n | A 1 ∩ A 2 … A n - 1 )

Percebe-se que se fizermos para cinco eventos iremos acrescentar um termo análogo a esse na expressão e assim por diante. Veja só o esquema abaixo:

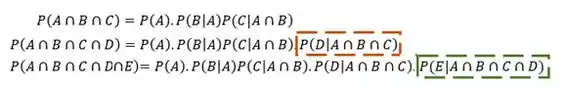
Notamos que esse é o termo que é acrescentado a nossa expressão. Assim podemos pensar no caso geral né?

Passo 3

Pro caso geral então teremos:

P A 1 ∩ A 2 ∩ A 3 … ∩ A n - 2 ∩ A n - 1 ∩ A n

= P A 1 . P A 1 . P A 1 ∩ A 2 … P A 1 ∩ A 2 … ∩ A n - 2 . P ( A n | A 1 ∩ A 2 … ∩ A n - 1  

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #6

Marcos Nascimento Magalhães e Antonio Carlos Pedroso de Lima, Noções de Probabilidade e Estatística, 6ª ed. São Paulo: Edusp, 2004

Sejam A,B e C pertencentes a um mesmo espaço amostral. Mostre que:

a) P A c B = 1 - P A B

b) P A ∪ B C = P A C + P B C - P A ∩ B C

Passo 1

Vamos lá! Uma coisa de cada vez

a) P A c B = 1 - P A B

Vamos desenvolver cada lado separadamente?

L.E: P A c B = P A c ∩ B P B

L.D.: P A B = P A ∩ B P B

P A c B = 1 - P A B →   P A c ∩ B P B = 1 - P A ∩ B P B

Bom, vamos supor que essa equação é verdadeira. Se for podemos passar tudo que for letra pra um lado e tudo o que for número (no caso só o 1 mesmo hehe) pro outro certo?

  P A c ∩ B P B + P A ∩ B P B = 1

Passo 2

Agora vamos mexer nessa equação!

Como tem o mesmo denominador, vamos juntar o numerador:

  P A c ∩ B + P A ∩ B P B = 1

Epa! Essa soma aí.. Podemos escrever como:

P ( A c ∩ B ∪ A ∩ B ) P B = 1  

Agora se liga no diagrama:

Esses são os nossos eventos. Como não sabemos se eles são disjuntos ou não, colocamos o caso mais abrangente, ou seja, quando ele possuem interseção.

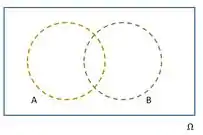
Vamos mostrar agora: A c ∩ B

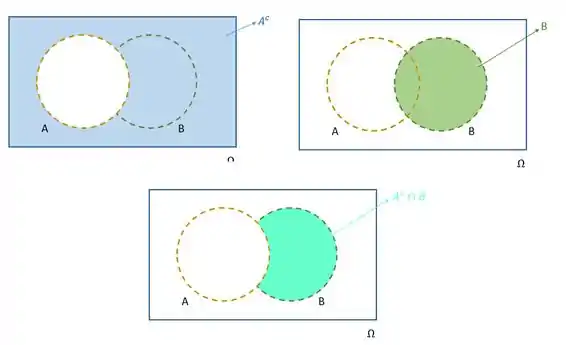
E A ∩ B :

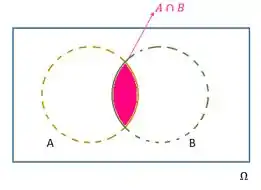
Com o diagrama conseguimos notar que :

A c ∩ B ∪ A ∩ B = B

Assim temos que:

P ( B ) P B = 1 = 1

Passo 3

b) P A ∪ B C = P A C + P B C - P A ∩ B C

Vamos olhar para cada lado separadamente:

Lado esquerdo:

P A ∪ B C = P A ∪ B ∩ C P C

Lado direito:

P A C + P B C - P A ∩ B C

Olhando para cada termo:

P A C = P A ∩ C P C

P B C = P B ∩ C P C

P A ∩ B C = P A ∩ B ∩ C P C  

Teremos assim no lado direito:

P A ∩ C P C + P B ∩ C P C - P A ∩ B ∩ C P C

Reescrevendo a expressão:

P A ∪ B ∩ C P C = P A ∩ C P C + P B ∩ C P C - P A ∩ B ∩ C P C

Supondo ser verdadeira essa expressão, vamos mudar de lado o termo negativo, lembrando de trocar o sinal:

P A ∪ B ∩ C P C +   P A ∩ B ∩ C P C = P A ∩ C P C + P B ∩ C P C

A ∪ B ∩ C ∪ [ A ∩ B ∩ C ) ] = ( A ∩ C ) ∪ ( B ∩ C )

Vamos olhar para o diagrama para ver se é verdade:

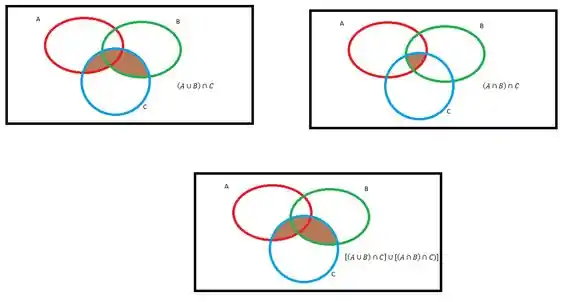
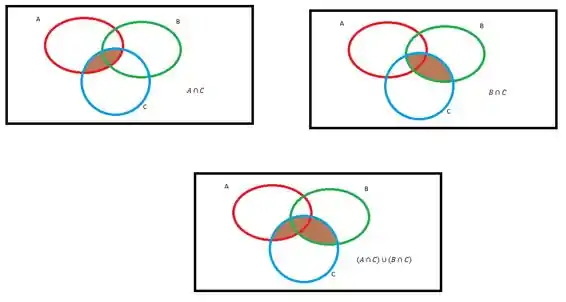
Logo é verdadeiro!

Resposta

a) Verdadeira

b) Verdadeira

Exercícios de Livros Relacionados

Verifique pelas Eqs. (3.2) que, sendo A fixo, P ( B | A ) satisfaz aos vários postulados da probabilidade.
Um artigo na British Medical Journal “Comparison of treatment of renal calculi by operative surgery, percutaneous nephrolithotomy, and extracorporeal shock wave lithotripsy” - Comparação de tratamento
A urna 1 contém x bolas brancas e y bolas vermelhas. A urna 2 contém z bolas brancas e v bolas vermelhas. Uma bola é escolhida ao acaso da urna 1 , e posta na urna 2 . A seguir, uma bola é escolhida a
Demonstre: Se P (A| B )P (A) , então P (B| A )P (B) .
Um mecanismo pode ser posto em uma dentre quatro posições: a ,b ,c e d . Existem 8 desses mecanismos incluídos em um sistema. ( a ) De quantas maneiras esse sistema pode ser disposto? ( b ) Admita que