Cálculo de Probabilidades - Arranjo & Combinação
Teoria
Introdução
Imagina que temos a seguinte situação:
Em uma empresa, um grupo de 5 funcionários se candidataram para as vagas de Diretor, Gerente Geral e Secretário Executivo. De quantas maneiras podemos preencher essas 3 vagas?
Para resolver esse problema utilizaremos a ideia de Arranjo!! Vamos ver com calma como funciona, beleza?!
Arranjo
Vamos ver então como funciona essa parada de Arranjo!
Para resolver o problema acima vamos representar as vagas desse modo:
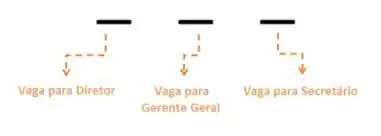
Temos 5 pessoas que se candidataram a todas as três vagas. Para começar a ocupar as vagas, temos que começar escolhendo um dos funcionários para ocupar algum dos cargos, nesse caso vamos começar pelo cargo de diretor:
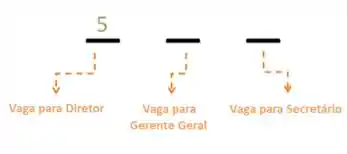
Restaram então 4 pessoas para ocupar os cargos restantes, logo temos 4 opções para a vaga de Gerente real, visto que uma pessoa já foi escolhida para ser o diretor:
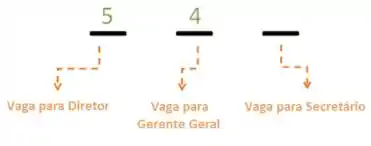
Sobram então tres opções de funcionários que concorrem pela vaga de Secretário:
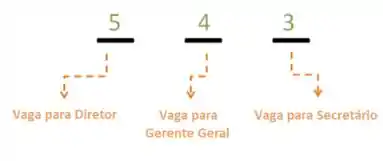
Cada escolha que fazemos gera várias possibilidades de ordens diferentes. Para contabilizar todos precisamos multiplicar cada escolha pelo número de possibilidades, ou seja PRINCÍPIO MULTIPLICATIVO!
Então temos
Ao pensarmos desse jeito já estamos considerando a permutação desses funcionários nos diferentes casos. Por exemplo:
Imagina que Joana, Laura e Bruna são três das 5 funcionárias que estão se candidatando para a empresa. Note que:
Isso acontece porque nesse caso, estamos levando em consideração a ordem das vagas oferecidas. Quando realizamos esse tipo de raciocínio, estamos fazendo um ARRANJO.
Mas como escrever isso para um caso geral?
Note que o método para calcular arranjos é muito parecido com o método para calcular permutações. A diferença que ao invés de permutar elementos completamente, só precisamos fazer as contas de acordo com o número de escolhas.
Logo precisamos dividir a permutação de elementos por
Essa é a fórmula geral para calcular arranjos, porém se preferir resolver seguindo os passos do exemplo não há problema, vai dar o mesmo resultado!
Vamos ver outro exemplo?
Exemplo
Em uma corrida há 10 atletas. De quantas maneiras diferentes podemos montar o pódio?
Nesse caso precisamos levar em consideração a ordem do 1°, 2° e 3° lugar, concorda?! Digamos que Pedro, Maria e João tenham sido os 3 primeiros colocados, respectivamente:
Isso é diferente se a ordem de chegada fosse:
Beleza?! Nesse cenário a ordem importa!!!
Então, temos que aplicar a fórmula do arranjo:
Tudo bem até aqui?
Combinação
Vamos estudar outra situação:
Em uma empresa, um grupo de 5 funcionários se candidataram para as 3 vagas de Diretor. De quantas maneiras podemos preencher essas 3 vagas?
A princípio pode parecer o mesmo problema anterior, certo? Mas veremos que existem algumas diferenças bem importantes! Temos 3 vagas, e 5 funcionários se candidatando porém, nesse caso, todas as vagas têm o mesmo cargo.
Para resolver esse problema precisamos simplesmente escolher 3 pessoas de um grupo de 5 para preencher as vagas. Para entender melhor a diferença imagina se Joana, Laura e Bruna são escolhidas novamente:
Isso acontece porque a ordem de escolhas não faz diferença! Se a Joana for escolhida primeiro e a Laura e Bruna em seguida, no final as três ainda serão diretoras.
Quando aplicamos esse tipo de raciocínio, estamos fazendo uma COMBINAÇÃO.
Ok, mas como calculamos isso?
Ao compararmos com o arranjo, percebemos que se quisermos escolher três pessoas para preencher essas vagas temos que tirar essas repetições que acontecem por conta da ordem não importar. No caso da Joana, Laura e Bruna, se permutarmos as três funcionárias teremos o número de repetições!
Logo, para descobrir de quantas maneiras podemos preencher essas 3 vagas, precisamos dividir a fórmula do arranjo por
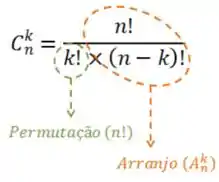
Para descobrir a combinação (Combinação de 3 elementos de 5) precisamos:
Lembre-se: Em combinação não importa a ordem!
Vamos para mais um exemplo rápido?
Para calcular de quantas maneiras podemos escolher cinco livros de um total de dez, faremos?
Nesse caso a ordem não importa! Então:
Tudo bem?
E como juntamos tudo isso que estamos vendo com o Cálculo de Probabilidades?
O cálculo dos Arranjos e Combinações que estamos vendo aqui são para saber a quantidade de eventos possíveis de um espaço amostral. Dessa forma, se tivermos algum caso de Cálculo de Probabilidades com Arranjo ou Combinação, basta utilizar a fórmula abaixo:
Onde o numerador é a quantidade de eventos possíveis (arranjos ou combinações calculadas) e o denominador o espaço amostral. Show de bola?!
Agora vamos praticar!
Exemplo
Exercícios Resolvidos
Exercício Resolvido #1
Gelson Iezzi, Osvaldo Dolce, David Degenszajn e Roberto Périgo, Matemática, 2ª ed
De um baralho de 52 cartas extraímos quatro simultaneamente.
a) Quantas são as possibilidades de sorteio das cartas?
b) Quantos resultados apresentam, entre as cartas sorteadas, o rei de espadas?
c) Quantos resultados apresentam exatamente dois ases?
Passo 1
Em um baralho de 52 cartas extraímos quatro simultaneamente, ou seja, a ordem não importa! Quando a ordem nãi importa em geral usamos Combinação.
Passo 2
a) Ele quer saber quantas são as POSSIBILIDADES e não as PROBABILIDADES. Olharemos apenas para o evento.
Evento A: Sorteio de 4 cartas de um baralho de um total de 52.
De quantas formas podemos retirar 4 cartas de um baralho de 52? Essa é exatamente a pergunta respondida pela fórmula da combinação! Nesse caso, :
Passo 3
b) Quantos resultados apresentam, entre as cartas sorteadas, o rei de espadas?
Olhando novamente para o nosso evento:
Evento B: Entre as quatro cartas sorteadas queremos ter o Rei de Espadas.
Neste caso temos que uma das quatro cartas já está definida (Rei de Espadas), enquanto as outras 3 não estão. Temos que sortear essas outras 3, de um total agora de 51 cartas!. Então o resultado será
Ou seja, temos 20.825 possíveis resultados, onde ao retiramos 4 cartas do baralho, uma delas seja um Rei de Espadas.
Passo 4
c) Quantos resultados apresentam exatamente dois ases?
Em um baralho temos 4 ases. Nesse caso queremos resultados com exatamente dois ases. Ou seja, a primeira coisa que devemos fazer é escolher dentre os quatro quais dois irão aparecer. Precisamos saber de quantas formas isso pode acontecer, que é exatamente a combinação :
Agora que já escolhemos quais as irão compor nossa retirada vamos pensar nas outras cartas.
O nosso baralho não tem agora 52 cartas. Temos que descontar os ases, portanto teremos 48 cartas. Ué, mas por que estamos descontando 4 ases?!
Descontamos os 4 ases pois queremos APENAS dois na nossa retirada, então temos 2 já sendo utilizados e os dois restantes NÃO PODEM SER possibilidades de retirada, senão, poderíamos vir a ter mais de exatamente dois ases, e não é isso que a questão quer!
Teremos assim, uma combinação de 2 cartas, entre 48 cartas totais (que com certeza não são ases, pois descontamos todos eles):
Finalmente, multiplicamos os resultados para ter o total (porque estamos primeiro selecionando os ases, e depois de selecionados, a gente selecionou o resto das cartas princípio multiplicativo)
Resposta
Exercício Resolvido #2
IME – Lista de Exercícios I – Professores Aderson Passos, Paulo Henrique Maranhão e Luis Antônio Seabra – Questão 19
Um banco possui um cofre que possui uma tranca com combinação. A tranca requer oito diferentes inteiros entre 1 e 90, que devem ser colocados em qualquer ordem. Entretanto, a tranca permite que 10 inteiros diferentes variando entre 1 e 90 sejam utilizados como uma combinação, ou seja, a tranca abrirá se 8 dos 10 números da combinação forem colocados. Encontre a probabilidade de que um ladrão abra a porta na primeira tentativa.
Passo 1
Vamos láá!! Queremos encontrar a probabilidade de que um ladrão abra a porta na primeira tentiva, beleza?!
Para saber a probabilidade de abrir de primeira o cofre faremos:
Concorda?!
Então vamos achar o nosso espaço amostral e nosso evento!
Passo 2
A questão diz que pra montar a senha desse cofre podemos escolher números de 1 até 90 (90 possibilidades) e que temos que escolher 8 números.
Então de 90 escolhemos 8, certo?
Essas são todas as possibilidades, ou seja, nosso espaço amostral :)
Passo 3
O enunciado diz também que se digitarmos 10 números e 8 desses forem a chave do cofre, conseguimos acessa-lo. Então de 10 números precisamos acertar apenas 8, ou seja, escolher 8.
Esse é o nosso evento, certo?!
Passo 4
Agora, para saber a probabilidade de abrir de primeira o cofre faremos:
Beleza, agora vamos calcular esse valor lembrando da fórmula para a combinação!
Por fim, agora é só fazer a probabilidade.
Ou seja, mesmo com toda essa facilidade de poder escolher dez números, seria bem difícil esse ladrão conseguir abrir a tranca na primeira tentativa rs.
Resposta
Exercício Resolvido #3
Lista RUMO AO ITA - FUNIVERSA – 2009-IPHAN-ANALISTA
Em um instituto de pesquisa trabalham, entre outros funcionários, 3 físicos, 6 biólogos e 2 matemáticos. Deseja-se formar uma equipe com 4 desses 11 estudiosos, para realizar uma pesquisa. Se essa equipe for composta escolhendo-se os pesquisadores de forma aleatória, a probabilidade de todos os físicos serem escolhidos é um número cujo valor está compreendido entre:
a)0,00 e 0,01
b)0,01 e 0,02
c)0,02 e 0,03
d)0,03 e 0,04
e) 0,04 e 0,05
Passo 1
Vamos usar a fórmula
Onde
número de casos favoráveis
número de casos possíveis
Passo 2
Vamos ver primeiro o número de casos possíveis:
Temos uma equipe de 11 estudiosos no total e queremos montar um grupo de quatro pessoas aleatoriamente, sem importar a ordem, certo? Então de 11 escolheremos 4.
Esse é o número de casos possíveis..
Passo 3
Agora vamos olhar para o número de casos favoráveis: todos os físicos na equipe.
Temos um total de 3 físicos e 8 de outras disciplinas. Como preciso na minha equipe de 4 pessoas, teremos:
- 3 físicos Escolher 3 físicos entre os 3 físicos
- 1 qualquer outra matéria Escolher uma pessoa dentre as 8 restantes
Agora basta multiplicar as duas (isso porque primeiro estamos escolhendo os físicos e depois o restante):
Passo 4
A probabilidade será dada por:
Resposta
Letra C