Teorema da Probabilidade Total
Teoria
O Teorema da Probabilidade Total é um teorema fundamental dentro do Cálculo de Probabilidades, que relaciona probabilidades condicionais com probabilidades marginais.
Vem comigo aprender sobre esse teorema!
A definição formal do teorema da probabilidade total é a seguinte.
Seja
Seja sincero, você entendeu alguma coisa? hahaha
Calma, vou te explicar de onde veio isso aí.
Vamos supor que temos um espaço amostral
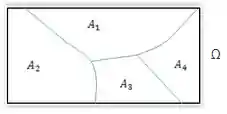
Agora considere um evento qualquer
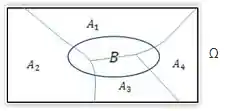
Presta atenção nesses eventos aqui:
Note que eles também são mutuamente exclusivos, e assim sendo, podemos escrever o evento
Escrito dessa forma, a probabilidade de
Podemos substituir cada uma dessas probabilidades da interseção pela probabilidade condicional:
Sendo assim:
E isso, podemos escrever como um somatório:
E é daí que tiramos o Teorema da Probabilidade Total. Fez mais sentido agora né?
Vamos fazer um exemplo pra ficar ainda mais claro.
Um velejador experiente tem 50% de chance de vencer uma regata sob vento forte, porém sem a presença de vento forte, suas chances caem para 25%. As autoridades do serviço de meteorologia da cidade que sediará a próxima regata estimam em 30% a probabilidade de que ocorra vento forte durante a competição. Sabendo disso, qual a probabilidade do velejador ser o vencedor ?
Vamos fazer um passo a passo para resolver essa questão.
PASSO 1
Definir os eventos:
IMPORTANTE: Note que os eventos
PASSO 2
Anotar as probabilidades dadas no enunciado:
PASSO 3
Temos
E aí? Acha que foi?
Vamos treinar mais um pouco com os exercícios, beleza?
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ, ProbEst, P1/2014.1, 1
Três pesquisadores pensam, de forma independente, na solução de um problema. Pela experiência e conhecimento de cada pesquisador sabe-se que as probabilidades de encontrar a solução são de para A, de para B e de para C . Calcule a probabilidade:
- de que o problema seja resolvido;
- de pelo menos dois dos três pesquisadores resolverem o problema;
- condicional de B resolver o problema dado que este foi resolvido por pelo menos dois pesquisadores.
Passo 1
Inicialmente, vamos nomear os nossos eventos.
Anotamos também os dados do enunciado:
Passo 2
(a)
Vamos ter que calcular a prob. do problema ser resolvido,
Com as informações que temos no enunciado iremos utilizar o caminho do complementar para resolver essa questão. Como assim? Vou te explicar agora!!
A gente sabe que a prob. do problema ser resolvido é 1 menos a prob. de ele não ser resolvido.
Concorda?!
Fazemos dessa forma porque conseguimos calcular a probabilidade de nem o , nem o e nem o resolverem a questão... Vamos ver como vai funcionar?!
Passo 3
A prob. é a prob. de nem o , nem o e nem o resolverem a questão;
Temos que
e
Assim, vamos ter que será a interseção desses três:
Beleza?!
Passo 4
Com isso podemos substituir e encontrar o que queremos.
Então a probabilidade do problema ser resolvido é de 60%.
Passo 5
(b)
Bom, vamos calcular agora .
Teremos os seguintes casos de pelo menos dois dentre os três resolverem a questão:
Logo, A prob. de pelo menos dois dentre os três resolverem a questão será:
Como os eventos são mutuamente exclusivos (não haverá interseção entre eles pois as pesquisas são independentes) é só calcular cada interseção e somar.
Passo 6
Calculando cada parcela:
Então:
Passo 7
(c)
Aqui queremos calcular a condicional de B resolver o problema dado que este foi resolvido por pelo menos dois pesquisadores. Ou seja, vamos utilizar a probabilidade condicional rs.
Queremos .
O valor de nós já temos.
Beleza?!
Passo 8
Basta calcularmos .
Vimos há alguns passos atrás que
Aqui só vamos pegar aqueles que contenham B, beleza?!
Então,
Concorda? A probabilidade de ser um dos que resolveu o problema é isso aí mesmo num é? Beleza então.
Usando os valores que a gente já calculou no passo 6.
Passo 9
Agora é só substituir na fórmula da prob. Condicional:
Resposta
Exercício Resolvido #2
UERJ-L1-PROF FABIANO-14
Cada uma de 3 caixas possui 2 gavetas. A primeira caixa contém uma moeda de ouro em cada gaveta, a segunda caixa contém 2 moedas de prata em cada gaveta, e a terceira caixa, uma moeda de ouro em uma gaveta, e uma de prata na outra. Uma caixa é escolhida ao acaso; uma de suas gavetas é escolhida ao acaso e aberta, encontrando-se uma moeda de ouro. Qual a probabilidade que a moeda da outra gaveta seja também de ouro?
Passo 1
Vamos chamar de:
Passo 2
Usando probabilidade condicional a gente sabe que a probabilidade da segunda moeda ser de ouro sabendo que a primeira já foi de ouro é dada pela fórmula:
E é exatamente isso que a gente precisa calcular.
Passo 3
Vamos por partes.
é a probabilidade da primeira e da segunda moeda serem de ouro, certo?
Só que isso só acontece se escolherem a caixa I, concorda?
Então:
Passo 4
Agora temos que calcular a probabilidade da primeira moeda ser de ouro.
Pra isso, vamos usar o teorema da probabilidade total.
Probabilidade da primeira moeda ser de ouro é a prob. da primeira ser de ouro sabendo que escolhemos a caixa I vezes a probabilidade de escolhermos a caixa I, mais a prob. da primeira ser de ouro sabendo que escolhemos a caixa II vezes a prob. de escolhermos a caixa II e a mesma coisa pra III.
Como todas as moedas da caixa I são de ouro
Como na II não temos moedas de ouro
E na III temos uma de ouro
E a probabilidade de ser escolher qualquer caixa é:
Passo 5
Agora só substituir na fórmula:
E:
Que era exatamente o que a gente queria.
Resposta
Exercício Resolvido #3
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006,44-125
Os colégios A, B e C têm as seguintes porcentagens de rapazes, respectivamente: 40%, 20% e 10%. Um desses colégios é selecionado ao acaso e oito alunos são escolhidos, com reposição. Se o resultado for RRRMMMMM (R para rapaz e M para moça), qual é a probabilidade de ter sido selecionado o colégio C?
Passo 1
Primeira coisa que iremos fazer é anotar os dados do enunciado
Colégios
- A : 40% rapazes 60% moças (Utilizamos o complementar)
- B: 20% rapazes 80% moças
- C: 10% rapazes 90% moças.
Evento D: Oito alunos são escolhidos ao acaso com reposição, sendo o resultado:
RRRMMMMM
Quero saber: Qual a probabilidade de ter sido selecionado o colégio C, dado esse resultado o sorteio?
Ou seja, quero saber
Passo 2
Sabemos que:
Precisamos então calcular:
e
Passo 3
Cálculo de
Queremos saber a probabilidade de ter retirado três rapazes e cinco moças na escola C.
Cálculo de P(D)
Vamos utilizar o Teorema da Probabilidade Total:
E quem será
É a probabilidade de ter sorteado três rapazes e cinco moças na escola A.
E ?
Assim:
Substituindo teremos:
Resposta
0,072
Exercício Resolvido #4
UFRJ-P1-2012.2.-1(b)(c)
Para competir em uma certa regata as embarcações podem velejar com no máximo 4 tripulantes. Os tripulantes de cada embarcação são inscritos previamente e não podem ser alterados mais tarde. A embarcação Chez Moi, participante da regata, inscreveu Alberto, Bernardo, Carlos e Diogo. Carlos e Diogo confirmaram a presença na regata com probabilidade 100%. A probabilidade de Alberto comparecer à regata é 50%, enquanto que a de Bernardo, é 70%. A decisão de comparecer ou não por parte de Alberto não influencia a decisão de comparecer ou não por parte de Bernardo e vice versa. Note que o fato do número de velejadores no barco poder ser igual a 2, 3 ou 4 caracteriza uma partição do espaço amostral. Com a tripulação completa, a embarcação Chez Moi tem 80% de probabilidade de vencer a regata; com apenas Carlos e Diogo, esta probabilidade cai para 20%; e com três tripulantes a probabilidade de vencer é de 50%. Pede-se calcular a probabilidade de que:
- pelo menos um dos velejadores, Alberto ou Bernardo, compareçam à regata;
- a embarcação Chez Moi vença a regata;
- pelo menos um dos velejadores, Alberto ou Bernardo, tenham comparecido à regata condicionado ao fato de que a embarcação Chez Moi venceu a regata. Compare suas respostas dadas nos itens (b) e (c). A probabilidade aumentou ou diminuiu? Por que?
Passo 1
(a)
Vamos chamar de:
A gente sabe que:
A probabilidade de pelo menos um deles comparecer é dada por:
Passo 2
(b)
Chamando de:
A gente precisa calcular .
Existem 4 situações pra participação da regata.
Passo 3
Pra calcular vamos usar o teorema da probabilidade total, levando em consideração as 4 situações discritas.
Se você ler com atenção o enunciado vai perceber que temos todos esses valores, lembrando que e são independentes e que e .
Passo 4
Do enunciado, a gente tira que:
Substituindo os valores:
Passo 5
(c)
Agora a gente tem que calcular .
Vamos usar prob. Condicional aqui.
Sendo que:
E:
É a probabilidade do barco vencer a regata e Bernardo ou Alberto estarem presentes, que foram calculadas como parcelas na hora que a gente calculou a probabilidade total do barco vencer a regata.
Substituindo os valores:
Resposta
Exercício Resolvido #5
Elaboração Própria
Um modelo de motor é fabricado por 3 fábricas: A, B e C. Sabe-se que A produz o dobro de motores que B e que B e C produzem o mesmo número de motores. Sabe-se ainda que 2% das dos motores produzidos por A e por B são defeituosos, enquanto que 4% dos produzidos por C são defeituosos. Todos os motores produzidos são misturados e colocados em um depósito. Se do depósito for retirada um motor ao acaso, qual a probabilidade de que ele seja defeituoso?
Passo 1
Vamos começar nomeando alguns eventos para nos organizarmos melhor:
É falado que A produz o dobro de motores que B produz, e B por outro lado produz o mesmo número de motores que C. Então podemos afirmar que A também possui o dobro de C. Então proporcionalmente podemos dizer:
Também é dado pra gente as probabilidades de defeito para cada empresa, que nada mais são que probabilidades condicionais, certo? Afinal, estão dando uma probabilidade de defeito “dado que o motor veio de tal empresa...”. Elas são:
Passo 2
Ok! Mas a questão quer saber a probabilidade da amostra sorteada ser defeituosa. Pelo teorema da probabilidade total calculamos essa probabilidade fazendo:
Aqui também podemos lembrar dos significados da multiplicação e da adição de probabilidades! Quando multiplicamos estamos falando de um evento E outro acontecerem, e quando somamos estamos falando de um evento OU outro acontecerem. E para ter a probabilidade do motor ser defeituoso é isso aí que escrevemos né?
“A probabilidade do motor vir de A E ser defeituoso (sabendo que veio de A), OU a probabilidade do motor vir de B E ser defeituoso (sabendo que veio de B), OU a probabilidade de vir de C E ser defeituoso (sabendo que veio de C).”
Dessa forma estamos incluindo todas as possíveis origens de um motor defeituoso!
Agora voltando a nossa equação, vamos substuitir com os valores achados no Passo 1: