Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 5.Exercícios Suplementares - Ex. 77
Uma loja de comida saudável possui duas marcas diferentes de um certo tipo de grão. Sejam = quantidade (lb) da marca em estoque e = quantidade da marca B em estoque. Suponha que a fdp conjunta de e seja
a. Desenhe a região de densidade positiva e determine o valor de .
b. e são independentes? Responda, encontrando primeiro a fdp marginal de cada variável.
c. Calcule .
d. Qual é a quantidade total esperada desse grão em estoque?
e. Calcule e .
f. Qual é a variância da quantidade total de grão em estoque?
Passo 1
Falaaa, meu querido/minha querida. Como vai?? Nessa questão vamos precisar calcular bastante coisa, então, bora deixar de enrolação e irmos para os cálculos!!
Passo 2
A região de densidade positiva é representada por:
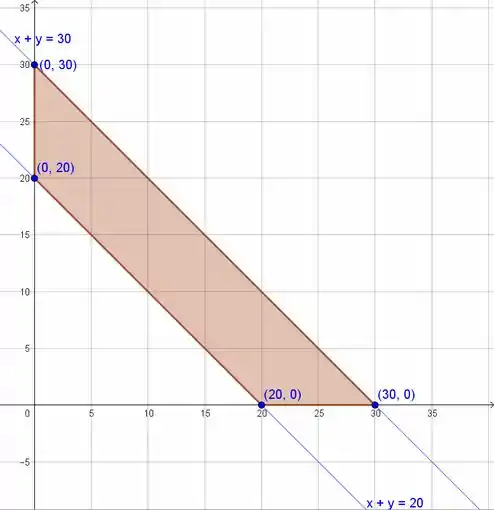
Para encontrarmos o valor de , precisamos definir a fdp sobre a região dada quando e depois quando .
Definindo quando .
Determinando quando .
A integral total da fdp conjunta sobre a região indicada é a soma das integrais que calculamos.
Por fim, a fdp conjunta só é válida se a integral total for igual a 1.
Passo 3
A fdp marginal de é a integral da fdp conjunta sobre todos os valores possíveis de .
Para .
Agora, para .
Logo, temos que a fdp marginal é:
A distribuição marginal de é a mesma que a distribuição marginal de , pois, a fdp conjunta não muda quando troca e , nem a região.
Portanto, e não são independentes, porque se multiplicarmos as distribuições marginais, não resultará na fdp conjunta.
Passo 4
Determinando a fdp conjunta para quando .
Para quando .
Por fim, a probabilidade total é a soma das duas probabilidades calculadas.
Passo 5
O valor esperado de é então integral do produto de todos os valores possíveis e a fdp conjunta.
Determinando a integral da fdp conjunta para .
Determinando a integral da fdp conjunta para .
O valor esperado total é a soma dos dois valores esperados.
Passo 6
Para determinarmos e , precisamos antes encontrar a média, o valor esperado de e a variância. Bora lá!!!
A média:
O valor esperado de .
Por fim, a variância é:
Agora sim, podemos calcular a covariância e a correlação.
A covariância é o valor esperado de subtraído pelo produto das duas médias.
E a correlação é a covariância dividida pelo produto dos desvios padrão.
Passo 7
Finalmente, estamos terminando!!!
A variância é o valor esperado do desvio da média. A média foi determinada na parte (d). Este valor esperado pode ser determinado de forma semelhante:
Resposta
- Resolução no passo 3.