Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 3.Exercícios - Ex. 54

Uma moeda é jogada duas vezes. Considere Z o número de caras na primeira jogada e W o número total de caras nas duas jogadas. Se a moeda não for equilibrada, tal que cara tem 40% de chance de ocorrer, determine

(a) a distribuição de probabilidade conjunta de Z e W;

(b) a distribuição marginal de Z;

(c) a distribuição marginal de W;

(d) a probabilidade de que pelo menos uma cara ocorra.

Passo 1

Falaaa, meu querido/minha querida. Pela definição da questão as variáveis aleatórias são Z e W , e Z pode assumir os valores 0 e 1 , enquanto W assume os valores 0 , 1 e 2 .

Então, bora realizar a questão!!!

Passo 2

Podemos observar que quando Z = 1 , ou seja, o resultado do primeiro lançamento da moeda é cara, temos W ≥ 1 ou W ≠ 0 . Então:

f 1 ,   0 = P Z = 1 ,   W = 0 = 0

De forma similar, se Z = 0 , ou seja, quando o resultado do primeiro lançamento é coroa, temos W ≤ 1 ou W ≠ 2 . Sendo assim:

f 0 ,   2 = P Z = 0 ,   W = 2 = 0

Vamos usar Y como a variável aleatória que assume o valor 1 se o segundo lançamento for cara e 0 se for coroa.

Sabendo que a moeda não é equilibrada, concluímos:

P Y = 1 = P Z = 1 = 0,4             e P Y = 0 = P Z = 0 = 0,6

Pela definição das variáveis aleatórias Y , Z e W , temos:

W = Y + Z

Agora, podemos calcular as probabilidades restantes:

f 1,1 = P Z = 1 ,   W = 1 = P Z = 1 ,   Y + Z = 1 = P ( Z = 1 ,   Y = 0 )

= P Z = 1 ∙ P Y = 0 = 0,4 ∙ 0,6 = 0,24

f 1 , 2 = P Z = 1 ,   W = 2 = P Z = 1 ,   Y + Z = 2 = P ( Z = 1 ,   Y = 1 )

= P Z = 1 ∙ P Y = 1 = 0,4 ∙ 0 , 4 = 0 , 16

f 0 , 0 = P Z = 0 ,   W = 0 = P Z = 0 ,   Y + Z = 0 = P ( Z = 0 ,   Y = 0 )

= P Z = 0 ∙ P Y = 0 = 0 , 6 ∙ 0,6 = 0 , 36

f 0 , 1 = P Z = 0 ,   W = 1 = P Z = 0 ,   Y + Z = 1 = P ( Z = 0 ,   Y = 1 )

= P Z = 0 ∙ P Y = 1 = 0 , 6 ∙ 0 , 4 = 0,24

Portanto, a distribuição de probabilidade conjunta é:

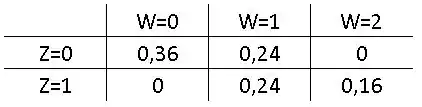
Passo 3

Estamos querendo encontrar h w = ∑ z f ( z ,   w ) . Usando a tabela, temos:

h 0 = ∑ z = 0 1 f z ,   0 = f 0 ,   0 + f 1 ,   0 = 0,36 + 0 = 0,36

h 1 = ∑ z = 0 1 f z ,   1 = f 0 ,   1 + f 1 ,   1 = 0,24 + 0,24 = 0,48

h 2 = ∑ z = 0 1 f z ,   2 = f 0 ,   2 + f 1 ,   2 = 0 + 0,16 = 0,16

Passo 4

Estamos querendo encontrar g z = ∑ w f ( z ,   w ) . Usando a tabela, temos:

g 0 = ∑ w = 0 2 f 0 ,   w = f 0 ,   0 + f 0 ,   1 + f 0 ,   2 = 0,36 + 0 , 24 + 0 = 0 , 6

g 1 = ∑ z = 0 2 f 1 ,   w = f 1 ,   1 + f 1 ,   1 + f 1 ,   2 = 0 + 0,24 + 0,16 = 0,4

Passo 5

Por fim, a probabilidade de ocorrer pelo menos 1 cara é a probabilidade do evento W ≥ 1 ocorrer.

P W ≥ 1 = 1 - P ( W < 1 )

= 1 - P ( W = 0 )

= 1 - h ( 0 )

= 1 - 0,36

P W ≥ 1 = 0,64

Resposta

Resolução nos passos anteriores.

Exercícios de Livros Relacionados

Suponha que, para certo indivíduo, a ingestão de calorias no café da manhã seja uma variável aleatória com valor esperado de 500 e desvio padrão de 50, a ingestão de calorias no almoço seja aleatória
Vimos que, se E X 1 = E X 2 =... =E X n = μ , então, E X 1 + … + X N = n μ . Em algumas aplicações, o número de X i s considerados não é um número fixo n, mas uma va N . Por exemplo: sejam N = o númer
Seja μ o pH real de um composto químico. Será feita uma seqüência de n determinações independentes do pH da amostra. Suponha que o pH de cada amostra seja uma variável aleatória com valor esperado μ e
O peso médio da bagagem de um passageiro da classe turística selecionado aleatoriamente, que voa entre duas cidades em uma determinada linha aérea, é 40 lb, e o desvio padrão é 10 lb. A média e o desv
Uma loja de comida saudável possui duas marcas diferentes de um certo tipo de grão. Sejam X = quantidade (lb) da marca A em estoque e Y = quantidade da marca B em estoque. Suponha que a fdp conjunta d