A seção de assistência técnica da Companhia MB tem cinco funcionários: e , cujos tempos de serviço na companhia são, respectivamente, um, três, cinco, cinco e sete anos.
- Faça um gráfico representando a distribuição de frequência dos tempos de serviço .
- Calcule a média a variância e a mediana
- Escreva os possíveis pares de funcionários para atender a ambos os pedidos.
- Para cada par, calcule o tempo médio de serviço - faça a distribuição de frequência e uma representação gráfica. Compare com o resultado de
- Calcule para os valores de os parâmetros ) e Compare com os resultados obtidos em Que tipo de conclusão você poderia tirar?
- Para cada par obtido em calcule a variância do par e indique-a por Faça a representação gráfica da distribuição dos valores de .
- Calcule e
- Indicando por a variável que expressa o tempo de serviço do funcionário que irá atender à firma Verde e o que irá atender à firma Azul, faça a distribuição conjunta da variável bidimensional
- As duas variáveis e são independentes?
- Você pode falar sobre as distribuições “marginais” de e ?
- Suponha agora que três firmas solicitem o serviço de assistência técnica. Quantas triplas podem ser formadas?
- Sem calcular todas as possibilidades, como você acha que ficaria o histograma de ? E ? E )?
- E sobre a variável ?
- A variável tridimensional teria alguma propriedade especial para as suas distribuições “marginais”?
Passo 1
Fazendo os itens temos:
O gráfico da alternativa é dado por:
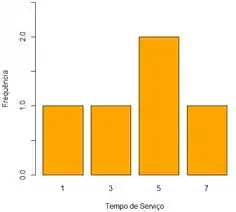
E para o item vamos, inicialmente, calcular a média aritmética dos dados:
Para encontrarmos a mediana, como se trata de um conjunto com um número ímpar de elementos, basta identificarmos o termo central. Neste caso:
Finalmente, vamos calcular a variância dos dados:
Passo 2
Em possíveis pares de funcionários para atender ambos os pedidos são:
E para o tempo médio de serviço para o par , por exemplo, é:
Vamos construir uma tabela de distribuição de frequências para

Passo 3
Em , vamos construir uma tabela para a distribuição de frequências de

E por fim,
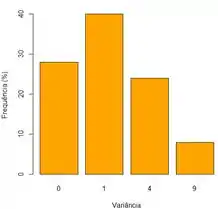
Passo 4
Em , temos e
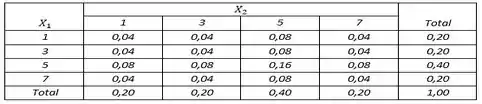
Em concluímos que as variáveis são independentes. Em concluímos que as distribuições “marginais” de e são iguais entre si e à distribuição da variável aleatória . Em poderão ser formadas triplas.
Em teremos um histograma cujo formato se assemelha à de uma curva normal. Em o histograma formado terá assimetria curvada para a direita.
Por fim, em como para a variável bidimensional ( , a variável tridimensional , irá ter distribuições marginais iguais à distribuição da variável aleatória
Resposta
Assim, conclui-se o desejado.