Exercícios de Gráfico de Barras, Setores & Histograma - Lista de Exercícios Resolvida
Questão 1
Considere os dados de Sexo e Raça para os dados abaixo: 
a) Construa a tabela de frequência para cada uma das variáveis.
b) Faça os gráficos de barras e de setores (pizza) para cada uma das variáveis.
Ver solução completaQuestão 2
Os dados abaixo representam o índice de alcalinidade de certa experiência.
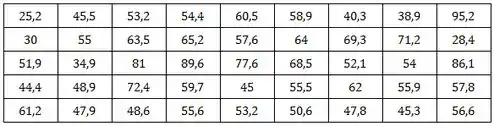
- Construa a distribuição de frequência para dados grupados (utilizando a Regra da Raiz)
- Encontre as Medidas de Posição.
- Encontre as Medidas de Dispersão.
- Construa Histograma e Polígono de frequência e analise a curva.
- Analise os resultados.
Questão 3
Os dados abaixo representam o índice de alcalinidade de certa experiência.
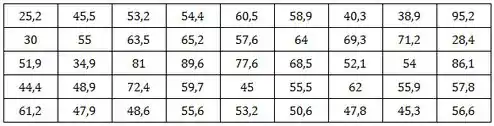
- Construa a distribuição de frequência para dados grupados (utilizando a Regra da Raiz)
- Construa Histograma e Polígono de frequência.
Questão 4
Os quadros abaixo correspondem aos resultados dos pesos dos alunos matriculados em uma das turmas na matéria de Probest 2013-2:
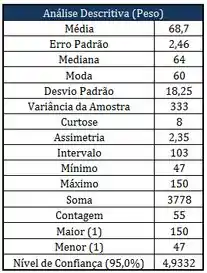
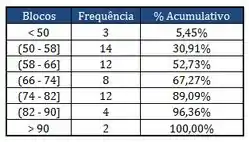
Com relação aos quadros apresentados acima, responda as perguntas:
- A quantidade de alunos com peso menor ou igual a .
- A quantidade de alunos com peso maiores de .
- Que tipo de simetria podemos verificar na amostra? Por quê?
- Com relação a Curtose, que tipo de curva podemos verificar na amostra? Por quê?
- Pelos dados da amostra, qual o coeficiente de variação?
- Pelos dados da amostra, qual o peso que mais se repete?
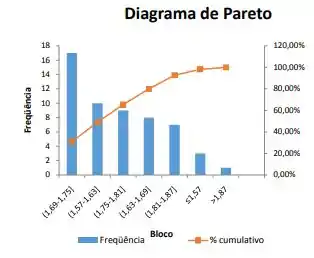
- Construa o diagrama de Pareto desta amostra, montando em blocos conforme o quadro do diagrama de frequência. Esboce os gráficos de frequência e cumulativo, mostrando os valores correspondentes.
Questão 5
Crie dois gráficos de barras, um com a frequência absoluta e outro com a frequência relativa, do número de alunos ausentes durante os cinco anos de curso na universidade.
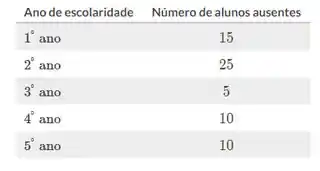
Questão 6
Os quadros abaixo correspondem aos resultados das notas finais, dos alunos matriculados no período passado na matéria PROBEST 2013-2:
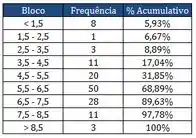
Com relação aos quadrados apresentados, responda as perguntas:
- O total de alunos que tiraram nota final menor ou igual 4,5 foram 11.
- 97,78% dos alunos tem média final menores ou iguais a 8,5.
- Pode-se dizer que a Assimetria “-1,26” é uma curva platicurtica.
- Quais são as medidas de Localização ou Tendência central?
- Quais são as medidas de Dispersão?
- Podemos dizer que a nota final 6,0 é a que mais vezes acontecem.
- O coeficiente de variação conforme a estatística descritiva é igual a 3,33.
- Construa o diagrama de Pareto desta amostra, montando em blocos conforme o quadro do diagrama de frequência. Esboce os gráficos de frequência e % cumulativo, mostrando os valores correspondentes.
V( ) ou F( )
V( ) ou F( )
V( ) ou F( )
V( ) ou F( )
V( ) ou F( )
Questão 7
Tomou-se uma amostra de estudantes que fizeram uma prova, e, a estatística descritiva, diagrama de frequência e gráfico de notas da prova estão a seguir:
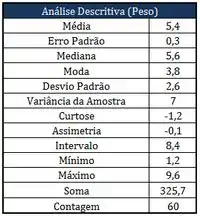
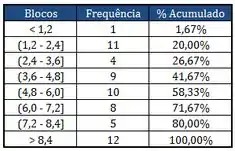
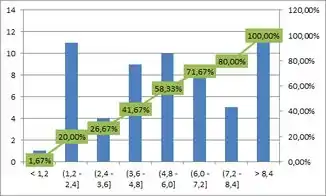
Com relação aos quadros apresentados da amostra das notas dos estudantes, avalie as seguintes afirmações como Verdadeira (V) ou Falsa (F):
- dos alunos tiraram notas menores ou igual a .
- das notas dos alunos estão entre e .
- Os valores da média e mediana permitem dizer que a distribuição é simétrica.
- Podemos dizer que dos alunos tiraram notas menores ou igual a .
- A assimetria negativa indica que existem mais notas altas e menos notas baixas.
- Podemos dizer que a nota é a que mais vezes acontece.
- O coeficiente de variação conforme a estatística descritiva é igual a .
- Construa o diagrama de Pareto desta amostra, montando em blocos conforme o diagrama de frequência acima (esboce o gráfico).
Questão 8
Observe a seguinte estatística descritiva referente a uma determinada amostra:
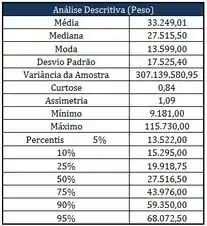
Com relação à estatística descritiva acima, responda as perguntas abaixo:
- Qual o coeficiente de variação da amostra?
- Qual a amplitude máxima da amostra?
- Assimetria positiva indica que existem mais valores altos do que baixos? Sim ou não?
- O que o coeficiente de curtose desta amostra nos permite dizer com relação a uma Normal?
- O que o percentil de desta amostra nos permite dizer?
- Qual é o valor que se repete mais vezes da amostra?
- Na tabela abaixo, temos o diagrama de frequência de uma de elementos onde: os intervalos são iguais; é o ponto médio de cada classe (intervalo); frequência absoluta simples; frequência cumulada. Preencher os espaços vazios do diagrama de frequência.
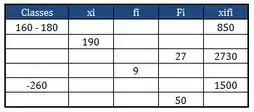
Questão 9
O quadro abaixo corresponde ao diagrama de frequências dos resultados das notas dos alunos matriculados em uma das turmas da matéria PROBEST_2016-2. Através dos dados apresentados, esboce o Diagrama de Pareto (gráfico com frequência e % cumulativo).
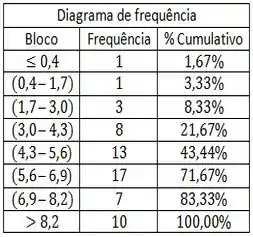
Questão 10
Os quadros abaixo correspondem aos resultados dos pesos dos alunos matriculados em uma das turmas na matéria de Probest 2013-2:
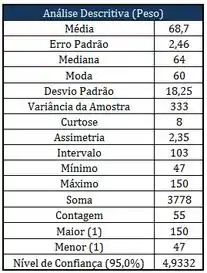
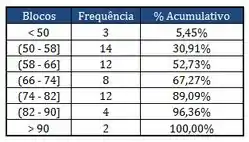
Com relação aos quadros apresentados acima, responda as perguntas:
- A quantidade de alunos com peso menor ou igual a .
- A quantidade de alunos com peso maiores de .
- Que tipo de simetria podemos verificar na amostra? Por quê?
- Com relação a Curtose, que tipo de curva podemos verificar na amostra? Por quê?
- Pelos dados da amostra, qual o coeficiente de variação?
- Pelos dados da amostra, qual o peso que mais se repete?
- Construa o diagrama de Pareto desta amostra, montando em blocos conforme o quadro do diagrama de frequência. Esboce os gráficos de frequência e cumulativo, mostrando os valores correspondentes.
Questão 11
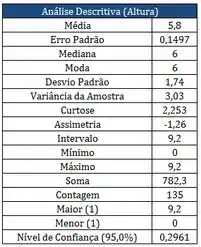
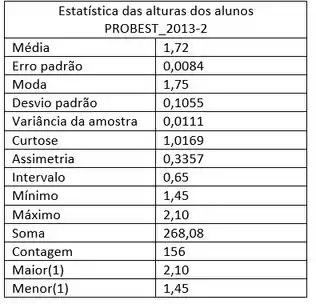
Tomou-se uma amostra de alunos matriculados em PROBEST 2013-2, e, são mostrados a seguir as alturas destes alunos através dos quadros: estatística descritiva, diagrama de frequências e histograma:
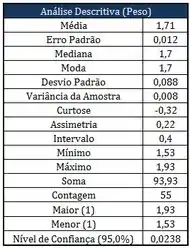
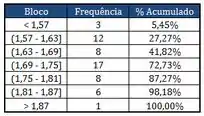
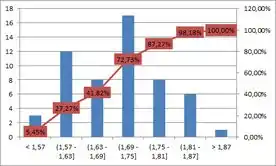
Com relação aos quadros apresentados da amostra das alturas dos alunos, avalie as seguintes afirmações como Verdadeira (V) ou Falso (F):
- dos alunos têm alturas menores ou iguais que .
- dos alunos têm alturas maiores que .
- Pode-se dizer que a distribuição é simétrica.
- Podemos dizer que alunos têm alturas menores ou iguais que .
- A assimetria indica que existem mais alturas altas e menos alturas baixas.
- Podemos dizer que a altura é a que mais vezes acontecem.
- O coeficiente de variação conforme a estatística descritiva é igual a
- Construa o diagrama de Pareto desta amostra, mostrando os blocos conforme o quadro do diagrama de frequências (esboce frequência e %cumulativo).
Questão 12
Os quadros abaixo estão relacionados às alturas dos alunos matriculados na disciplina PROBEST-2013-2. Através dos dados apresentados, pede-se:
- Esboce o Diagrama de Pareto (contendo tanto a frequência absoluta como a frequência acumulada (% cumulativo).
Questão 13
As tabelas na parte inferior correnspondem as alturas dos aulos matriculados na disciplina PROBEST-2013-2 turma 3VB. Usando os dados apresentados, pede-se:
- Através do diagrama de Pareto, construa o Diagrama de Frequência e o Histograma (Esboçe Gráficos de Frequência e % cumulativo).
- Se a probabilidade de um aluno de PROBEST faltar à aula é de , e supondo que os alunos faltem às aulas de maneira estatisticamente independentes entre si e no tempo, qual a chance de nessa turma o professor não ter nenhum aluno presente em determinado dia de aula?