Testes de Hipóteses - Introdução
Produzido por Jorge Alberto NascimentoTeoria
Introdução
Cara, vamos começar agora a falar de um assunto novo, e já te peço uma coisa: não pira! Vamos com calma e, no final, você vai estar entendendo tudinho.
Aviso logo que vamos usar algumas coisas lá de variáveis aleatórias como: Distribuição Normal, Padronização e Teorema Central do Limite. Se você não lembra muito bem dessas coisas, é uma boa dar uma olhadinha nesses tópicos, a gente tem esse conteúdo bonitinho aqui pra você. Agora, se você lembra desses paranauê aí, vem comigo!
Mas, afinal, o que é essa matéria? Até então estávamos estudando probabilidades, depois conhecemos a nossa querida estatística.... Agora eu quero saber se alguma afirmação, alguma hipótese que eu formulei, está correta. Como assim?
Se eu digo que:
“A estatura média dos assinantes do Responde Aí está acima de 1,73.”
Cara, se eu simplesmente falei isso aí, concorda comigo que a gente não sabe de cara se isso é verdade ou não? Ou seja, isso é uma hipótese!
Temos duas opções de decisão a tomar: aceitar ou rejeitar essa afirmação (hipótese), certo?
Essa tomada de decisão é justamente o teste de hipótese. É com isso que a gente vai começar a brincar agora! Vamos ter uma hipótese, e vamos querer descobrir se ela é verdadeira ou não.
Além disso, essa afirmação diz respeito a um parâmetro, que nesse nosso exemplo é a estatura média.
Opa, parâmetros! Lembra que nós já falamos sobre eles lá atrás também? Média populacional , variância populacional , ou até mesmo as amostrais como nossa variância amostral (. Esses carinhas aí vão ser muito importantes daqui pra frente, porque toda hipótese vai estar se referindo a algum deles.
Novamente vamos utilizar amostras para tirar conclusões da nossa população! Ou seja, com os parâmetros da amostra, vamos tomar uma decisão.
Hipótese Estatística
Pra não tomar nenhuma decisão precipitada, precisamos saber quem é o parâmetro que estamos avaliando. Além disso,se esse parâmetro é de uma população específica, também precisamos conhecer essa população.
E de que forma podemos conhecer uma população? Bom, vamos usar suas distribuições para representá-las! Voltando ao exemplo anterior...
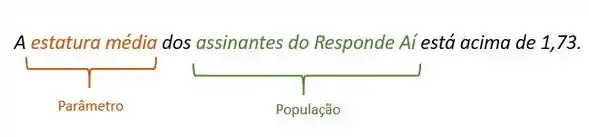
A população assinantes do Responde Aí pode seguir uma distribuição Normal, com uma média conhecida .
A hipótese será então sobre essa distribuição e envolverá, nesse caso, o parâmetro média.
Um outro exemplo:
“A taxa média de queima de um combustível usado para mover aeronaves é 50cm/s.”
- Taxa de queima: variável aleatória distribuição de probabilidade com média definida.
Estamos interessados em saber se essa afirmação é verdadeira ou não, ou seja, se a taxa média de queima é ou não.
Definição das Hipóteses
Cara, eu te disse que sempre vamos estar querendo provar se uma afirmação é verdadeira ou falsa, correto?
Logo, em qualquer teste de hipótese, vamos ter sempre duas hipóteses: a que concorda com a nossa afirmação inicial, que diz que ela é verdadeira, e uma hipótese que discorda dessa afirmação.
Essa hipótese que confirma uma afirmação recebe o nome de hipótese nula, e iremos denotá-la por .
No exemplo da taxa média de queima, nossa hipótese nula seria:
Ou seja, realmente o valor da média vale . A hipótese nula sempre vai conter o sinal de igualdade, beleza? Isso porque ela sempre vai ser a afirmação que queremos testar.
E qual seria a hipótese que diz o contrário disso? A hipótese que discorda da nossa afirmação é chamada de hipótese alternativa, e iremos denotá-la por .
Concorda comigo que, no nosso exemplo, poderíamos ter 3 tipos de hipóteses alternativas?
A nossa taxa média de queima pode ser simplesmente diferente de , pode ser maior do que , ou menor do que isso.
Tipos de Testes de Hipóteses
Percebeu que podemos ter diferentes tipos de hipóteses alternativas? Isso porque temos 3 tipos de testes de hipóteses! Vou te apresentar cada um deles agora.
Teste de Hipótese Bilateral
Vou reescrever aqui a afirmação que eu acabei de te dar no exemplo lá em cima:
“A taxa média de queima de um combustível usado para mover aeronavesé 50m/s.”
Bom, nossa hipótese nula vai sempre conter o sinal de igualdade (não esquece isso!). Logo, teremos que:
Até aí beleza. Vamos agora pro nosso divisor de águas: se a sua questão estiver falando de um teste de hipótese bilateral, sua hipótese alternativa será a seguinte:
Aqui que você precisa ter bastante atenção: no caso de um teste de hipótese bilateral, a hipótese alternativa sempre vai conter o sinal de diferença .
Ou seja, teremos que a taxa media de queima é diferente de .
Note que ser diferente de 50 significa que pode ser maior ou menor do que 50, por isso chamamos de bilateral.
Teste de Hipótese Unilateral
Aqui dentro do caso unilateral, vamos ter dois tipos: o unilateral inferior, e o unilateral superior.
Se você estiver em um teste de hipótese unilateral inferior, sua hipótese alternativa vai ser a seguinte:
Ou seja, se a taxa média de queima não é , aqui afirmamos que ela é menor do que isso na verdade.
Vai pelo nome do teste mesmo: como é inferior, o sinal aqui vai ser o de menor .
Já se você estivesse um teste de hipótese unilateral superior, sua hipótese alternativa seria essa:
Aqui afirmamos que na verdade a taxa média de queima é maior do que .
Aqui o sinal vai ser o de maior .
Cara, como essa parte de escrever as hipóteses é SUPER importante, e eu quero que você saiba isso de letra, vou te dar alguns exemplos maneiros aqui.
Na maior parte das vezes o enunciado não vai te contar se você está num teste bilateral ou unilateral, então você que vai ter que descobrir isso.
Ex. 1)“Um hospital alega que o tempo médio de resposta de sua ambulância é inferior a dez minutos. Formule as hipóteses para tomar uma decisão nesse problema.”
Bom, a primeira coisa é identificar nosso parâmetro. Como ele falou em tempo médio, nosso parâmetro populacional é o .
Vamos formular nossas hipóteses!
Hipótese Nula :
Estamos querendo testar sobre o tempo médio ser ou não , e a hipótese nula precisa sempre conter a igualdade!
Hipótese Alternativa :
Bom, precisamos contrariar nossa hipótese nula, e o enunciado nos disse que o hospital acredita que o tempo médio é inferior a . Logo, estamos em um teste de hipótese unilateral inferior!
Ex. 2) “Uma revista afirma que a proporção das chamadas telefônicas via celular feitas durante as tardes e os fins de semana é de 60%. Formule as hipóteses para tomar uma decisão nesse problema.”
Cara, o enunciado já disse pra gente que nosso parâmetro é a proporção , certo?
Vamos para as hipóteses então!
Hipótese Nula :
Estamos querendo testar sobre essa proporção de , e nosso precisa conter a igualdade.
Hipótese Alternativa :
Cara, só queremos testar se essa proporção é ou não é de . Logo, se for maior ou menor, já contrariamos nossa hipótese nula. Portanto, estamos num teste de hipótese bilateral!
Resumindo: Nossa hipótese nula é sempre afirmar que nosso parâmetro é igual a algum valor, e, caso essa afirmação seja falsa, vamos ter como discordar de três formas distintas: ou nosso parâmetro tem um valor diferente do valor que o enunciado deu, ou é maior, ou menor.
Obs1.: É importante ressaltar que as hipóteses serão sempre sobre a população, e não sobre a amostra. Contudo, iremos utilizar as informações das amostras para testar a hipótese.
Obs2.: A partir das informações que conseguimos com nossas amostras, vamos aprovar ou rejeitar nossas hipóteses, MAS sempre podemos errar na nossa decisão! Também podemos querer saber essa probabilidade de errar! (vamos ver isso nos próximos tópicos, relaxa!)
Regra de Decisão

E como vamos decidir afinal qual das duas hipóteses aceitar? Vamos entender isso melhor com um exemplo!
“Uma indústria compra ímãs importados, que devem satisfazer algumas exigências quanto a resistência à tração dos mesmos. Compramos majoritariamente de dois países (A e B) que possuem diferenças entre si.”
i) País A:
Resistência Média à tração: 145kg
ii) País B:
Resistência Média à tração: 155kg
“Um lote será leiloado e a empresa precisa saber qual país de origem para fazer a oferta. Uma amostra de 25 unidades é coletada. Pouco antes do leilão será divulgada a média amostral, . Qual regra de decisão deve ser usada para decidir se vem de A ou de B?”
Bom, temos uma empresa querendo comprar ímãs, e ela precisa saber de qual país vem esse ímã. Vamos identificar o que é o quê.
População: Ímãs
Amostra: Lote de 25 unidades dos ímãs
Parâmetro: Resistência média à tração.
Hipóteses:
O primeiro passo pra tomarmos nossa decisão, é sempre definir quais são nossas hipóteses!
Hipótese Nula
Vamos definir como nossa hipótese nula que a média da população é , ou seja, os ímãs são de origem do país B.
Hipótese Alternativa :
Precisamos de uma hipótese que contrarie a hipótese nula, então vamos dizer que a média é menor do que , e portanto os ímãs são de origem A.
Como definir a regra de decisão?
Cara, a regra de decisão nada mais é do que definir, com base em nossa amostra, qual hipótese estava correta.
Vamos considerar produtor aquele cuja média da amostra mais se aproximar do valor da média da população afirmado de cada país.
Uma possibilidade: escolhemos um ponto médio e afirmamos que se:
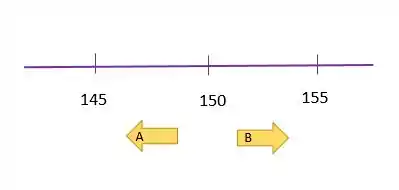
Nos próximos tópicos vou te contar que, para cada tipo de teste de hipótese, vamos ter um passo a passo pra descobrir nossa regra de decisão! Fica tranquilo, aqui só preciso que você entenda os conceitos.
Região Crítica:
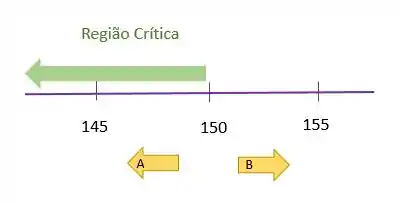
A região crítica é aquela que nos leva a rejeitar e aceitar . Vai ser sempre assim, não esquece isso!
Por exemplo, se tirássemos a média da nossa amostra (nosso querido ), qualquer valor menor do que faria com que rejeitássemos nossa hipótese nula .
Obs.: A região contrária à Região Crítica é a chamada Região de Aceitação.
Esse capítulo é só uma introdução mais conceitual mesmo, nos próximos vamos ver como isso tudo funciona na prática. =)
Definição das Hipóteses
Tipos de Testes de Hipóteses
Regra de Decisão
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Um professor afirma que a proporção de alunos que estudam na véspera da prova é maior que . Defina as hipóteses para testar a afirmação desse professor e classifique-a.
Passo 1
Vamos lá!! Se você reparar, o parâmetro analisado é a proporção populacional . Beleza?!
Dessa forma, precisamos testar a afirmação do professor, que diz que a proporção de alunos que estudam na véspera da prova é maior que , então, a hipótese nula vai concordar com o que ele está dizendo, porém sempre usando o sinal de :
Lembrando que igualdade dentro dos sinais de ou conta como igualdade! Aqui vamos escrever dessa forma pra ficar mais certinho com o enunciado. Mas vc poderia escrever só com se quisesse. O que realmente importa no teste de hipóteses é o sinal da hipótese alternativa!
E a alternativa tem que discordar disso aí:
Passo 2
Agora vamos relembrar: Existem 3 tipos de testes
- BILATERAL
- UNILATERAL INFERIOR
- UNILATERAL SUPERIOR.
Quem decide o tipo de teste é o sinal usado na construção da hipótese alternativa!
Se for é bilateral, se for é unilateral inferior e se for é unilateral superior!
Portanto, no nosso exercício ele será classificado como um teste de hipóteses unilateral inferior! Beleza?!
Resposta
Teste de hipóteses unilateral inferior
Exercício Resolvido #2
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006,330-05 - Modificada
A variável X, custo de manutenção de um tear, pode ser considerada como tendo distribuição normal de média e desvio padrão 20 unidades. Os valores possíveis de podem ser 200 ou 210. Para verificar qual dos dois é o mais provável, utiliza-se uma amostra de 25 teares. Defina:
a) Uma hipótese a ser estudada
b) Uma regra de decisão.
Passo 1
Vamos analisar a letra a)
Bom, nós temos 3 tipos diferentes de hipóteses: BILATERAL,UNILATERAL INFERIOR e UNILATERAL SUPERIOR.
Quem decide o tipo de teste é o sinal usado na construção da hipótese alternativa!
Se for é bilateral, se for é unilateral inferior e se for é unilateral superior!
Como o enunciado não diz nada diferente, podemos escolher de forma aleatória, concorda?! Então:
Beleza?!
Passo 2
b) Uma regra de decisão.
Vamos lá!! Como definir a regra de decisão?
Cara, a regra de decisão nada mais é do que definir, com base em nossa amostra, qual hipótese estava correta.
Uma possibilidade: Como estamos trabalhando com os valores 210 e 210, vamos escolher o ponto médio 205 como ponto crítico. Assim,
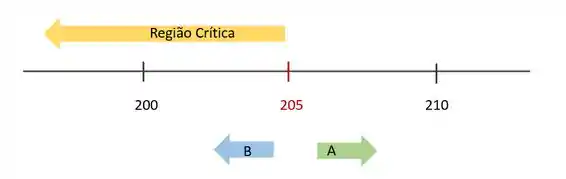
Ou seja, se a minha média amostral cair pra cima de 205 eu tenho que o produtor será , da mesma forma, se ele cair pra baixo ele vai ser do produtor
Lembrando que a região crítica é aquela que nos leva a rejeitar e aceitar . Vai ser sempre assim, não esquece isso!
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Elaboração Própria
Um vendedor afirma que a proporção de consumidores de sua loja que pagam com cartão é maior que . Defina as hipóteses para testar a afirmação desse vendedor e classifique-a.
Passo 1
O parâmetro analisado é a proporção populacional .
Precisamos testar a afirmação do vendedor, que diz que a proporção de consumidores que pagam com cartão é maior que , então, a hipótese nula vai concordar com o que ele está dizendo, porém sempre usando o sinal de :
Lembrando que igualdade dentro dos sinais de ou conta como igualdade! Aqui vamos escrever dessa forma pra ficar mais certinho com o enunciado. Mas vc poderia escrever só com se quisesse. O que realmente importa no teste de hipóteses é o sinal da hipótese alternativa!
E a alternativa tem que discordar disso aí:
Passo 2
Quando temos um teste com hipótese alternativa com sinal de , ele é classificado como um teste de hipóteses unilateral inferior!
Resposta
Teste de hipóteses unilateral inferior
Exercício Resolvido #4
Defina uma regra de decisão para decidir entre as seguintes hipóteses sobre a origem das peças de uma amostra que vão ser usadas numa fábrica:
Defina também a região crítica do seu teste de hipóteses.
Passo 1
A regra de decisão é sempre tomada a partir da nossa amostra. Se nossos testes envolvem o desvio padrão populacional , o parâmetro amostral que vamos usar na regra de decisão é o , que é o desvio padrão amostral.
Podemos tomar qualquer regra de decisão que seja minimamente conveniente. Por exemplo, nós sabemos que o desvio padrão populacional ser , significa que as peças tem origem A. Mas pode acontecer das peças da nossa terem origem A mas fugirem um pouquinho de , certo? Tipo, serem . Por que podem fugir? Porque é uma amostra, e erros sempre acontecem!
Então vamos estipular uma margem de erro qualquer para englobar possíveis erros do tipo. Vamos dizer que se o desvio padrão amostral estiver entre e , vamos tomar a decisão de que as peças da amostra tem origem A, estamos considerando então uma margem de erro de :
E para o contrário, vamos aceitar a hipótese alternativa:
Essas aí são possíveis regras de decisão que poderíamos tomar.
Passo 2
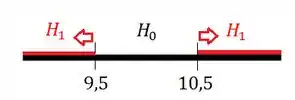
A região crítica é onde rejeitamos a hipótese nula, ou seja, é a região da regra de decisão que acabamos de descrever para quando aceitamos a hipótese alternativa:
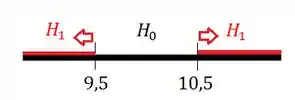
Essa área vermelha aí então é nossa
Resposta
Exercício Resolvido #5
Elaboração Própria
Um síndico de um condomínio diz que a média de energia usada pelas instalações comuns do condomínio por mês não passa de . Teste a afirmação deste síndico. Explique o que significa se nosso teste cair na região de aceitação.
Passo 1
Estamos falando do parâmetro média, então vamos testar nossa média populacional .
Como ele diz que a média não passa de , ou seja, é sempre menor ou igual a , e como sempre temos que incluir o na hipótese nula...
E a hipótese alternativa tem que contradizer isso aí e testar o que tá sendo pedido:
Passo 2
Se no final as nossas estatísticas de teste caírem na região de aceitação, significa que não vamos rejeitar a hipótese nula! Ou seja, vamos poder afirmar que realmente a média não passa de .