Fótons e Efeito Fotoelétrico
Teoria
Quantificação da energia
No modelo de Bohr, ao absorver energia o elétron pula de um nível da eletrosfera para outro.
OK. Mas se o “espaço” entre um nível e outro não é permitido, como ele passa de um nível para outro???
Quando ele já saiu de um nível, mas ainda não chegou no outro, onde ele tá? É tipo teletransporte?
A gente já comentou que alguns postulados de Bohr ainda são aceitos, enquanto outros estão comprovadamente errados. A quantificação da energia proposta por ele está entre os postulados ainda aceitos.
É como se o elétron só pudesse ficar em determinados níveis de energia. Estamos acostumados a pensar em uma rampa, ou seja, num aumento gradativo de energia. Mas para o elétron, a subida é via escada. Só os degraus são permitidos.
Em termos de energia é mais fácil de aceitar do que pensando em “trajetória” né?
Tipo... Tudo bem “subir os degraus de energia”, mas desaparecer num nível e aparecer no outro não pode?
A nossa tendência em aceitar uma explicação mais do que a outra é puramente porque estamos acostumados a pensar dessas formas. Nos tempos de Bohr, pensar em energia discreta (não contínua) parecia tão impossível quanto o elétron se teletransportar de um nível para o outro.
As coisas começaram a mudar com as observações das radiações dos corpos negros.
Radiação do Corpo Negro
Você já viu algo muito quente “brilhando”?
Quando um corpo negro é aquecido (muito aquecido), ele começa a “brilhar” (emitir radiação na forma de luz visível). Esse fenômeno é conhecido como incandescência.
A definição de corpo negro é essa mesma: um cara que emite radiação ao ser aquecido. E o nome negro é porque ele absorve todos os comprimentos de onda que incidem sobre ele, sem preferências!
Quando ele é aquecido, primeiro, ele tem um brilho avermelhado e, conforme a temperatura aumenta, o brilho passa a ser mais alaranjado, amarelado... até chegar num brilho branco.
Quando as radiações emitidas foram medidas, descobriu-se que, ao mudar de cor, não é que o corpo negro estivesse “deixando de emitir no vermelho e passando a emitir no amarelo”.
Quando o objeto era aquecido, ele passava a emitir mais em todos os comprimentos de onda. Ele estava emitindo mais no vermelho, mas ainda mais no amarelo.
Ou seja, conforme a temperatura aumenta, a intensidade da luz emitida também aumenta!
Mas como a gente quantifica essa emissão?
E Stefan-Boltzmann propôs que a intensidade de luz emitida era proporcional à temperatura na quarta potência:
Lei de Stefan-Boltzmann
Além disso, conforme a temperatura subia, o “máximo de emissão” se deslocava para comprimentos de onda cada vez menores (maior energia).
Wien observou que o produto entre o comprimento de onda de máxima absorção e a temperatura do corpo era sempre constante:
Lei de Wien
Os resultados observados eram esses:
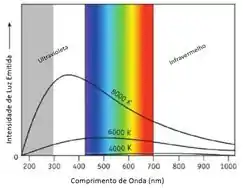
Tudo muito bom, tudo muito bem.
Mas, se tudo que a física clássica acreditava fosse verdade:
- Qualquer corpo fora do zero absoluto de temperatura () deveria brilhar (se tem temperatura, deveria ter intensidade luminosa!). Não existiria escuridão.
- Corpos muito quentes deveriam emitir em comprimentos de onda tão pequenos (raios X, gama, cósmicos) e t��o energéticos que destruiriam coisas ao redor deles. No gráfico de intensidade de luz emitida, aquela queda de intensidade no ultravioleta não deveria ocorrer.
A divergência entre o previsto pela física clássica e o observado experimentalmente na região do ultravioleta ficou conhecido como catástrofe do ultravioleta.
Os cientitas da época estavam se sentindo como a gente numa aula experimental: a teoria diz uma coisa, mas dá tudo ao contrário.
Fazer o que?! Se os resultados experimentais estão certos, só dá pra MUDAR A TEORIA!!!
Teoria de Planck
Planck foi o primeiro a propor que a energia só era passada de um corpo para o outro através de pequenos pacotinhos de energia.
Com isso:
- Corpos com baixa temperatura não “brilhavam”: como a energia não é contínua, não basta ter energia térmica para brilhar. O brilho só acontece depois de determinado patamar de energia.
- As emissões no ultravioleta (e em faixa ainda mais energéticas) não começam no 0 K e vão aumentando gradativamente. Elas só começam num patamar de temperatura altíssimo e aí sim acréscimos de temperatura geram acréscimos na intensidade de radiação emitida.
Lembra que a gente dividiu a matéria até chegar no átomo? Planck dividiu a energia até chegar no quantum.
Quantum é a menor quantidade de energia que pode ser emitida ou absorvida como radiação eletromagnética.
E por que você deve confiar nesse tal de Planck?
A teoria do cara funciona, explica várias paradas e prevê outras tantas.
Além disso, as ideias dele foram exploradas por ninguém mais, ninguém menos que Albert Einstein. Einstein provou a teoria de Planck estudando o efeito fotoelétrico e, aliás, ganhou um nobel por isso.
Se até Glorinha achou bacana, vamos dar uma olhada nesse efeito fotoelétrico aí.
Efeito Fotoelétrico
Efeito fotoelétrico é quando um metal emite elétrons ao ser atingido por uma radiação de determinada frequência.
Tipo assim:
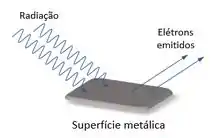
Os experimentos mostravam que ainda que a luz incidida fosse muito intensa, a emissão de elétrons só ocorria após atingida determinada frequência mínima.
Einstein se apropriou das ideias de Planck e foi além. Ele propôs que a radiação eletromagnética é feita de partículas.
Sim, amigos. A luz é feita de pequeníssimas partículas chamadas fótons.
E cada fóton pode ser entendido com um pequeníssimo pacote de energia.
A energia que um único fóton carrega é dada pela equação abaixo e depende da frequência desse fóton.
Onde é a constante de Planck e vale J.s, é a energia do fóton e é a frequência.
Assim:
- caso a frequência do fóton seja muito baixa, ele não tem energia suficiente para arrancar elétrons da superfície metálica, ainda que muitos fótons sejam incididos (alta intensidade luminosa);
- com a frequência adequada, mesmo a menor intensidade de luz é capaz de ejetar elétrons do metal;
- na frequência adequada, quanto maior a intensidade luminosa, maior o número de elétrons ejetados.
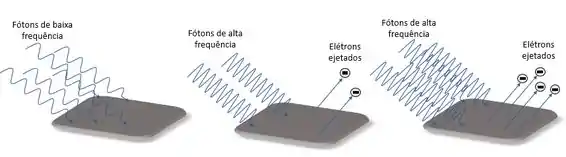
Calma que a gente já tá acabando.
Com a teoria do fóton, o efeito fotoelétrico funciona assim:
- a luz é absorvida pelos elétrons presentes no metal e a energia da luz aumenta a energia dos elétrons;
- o elétron está ligado ao metal por uma energia específica, chamada função trabalho do metal e simbolizada por (fi);
- quando a energia absorvida pelo elétron ultrapassa a energia específica que o liga ao resto do metal, ele é ejetado;
- se sobrar alguma energia depois que a função trabalho for superada, o excesso é convertido em energia cinética.
Como a energia cinética é:
Pelo efeito fotoelétrico, a energia cinética é aquela que foi dada ao elétron menos a que foi gasta para “soltar o elétron”.
Fechou?
Antes dos exercícios, um agradecimento especial pra Glória que permaneceu todo esse tópico com a gente.
E bora praticar!
Mas como a gente quantifica essa emissão?
Teoria de Planck
Efeito Fotoelétrico
Exercícios Resolvidos
Exercício Resolvido #1
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 9-exemplo 1.3.
Uma estrela pode ser considerada um corpo-negro, logo, podemos usar as aproximações do corpo-negro para medir sua temperatura. A intensidade máxima de radiação solar ocorre a 490 nm. Qual é a temperatura da atmosfera do Sol?
Passo 1
Lembra que, pela Lei de Wien, quanto maior a temperatura do corpo-negro, mais o comprimento de onda de emissão máxima se desloca para comprimentos de onda pequenos?
Vamos usar a Lei de Wien, então, pra determinar a temperatura do Sol!
Passo 2
Bora lá:
Particularmente, eu prefiro trabalhar com metros. Você faz como preferir/achar melhor.
Trabalhando com metros:
Pra quem é do time dos milímetros:
A gente considera o resultado como uma “boa aproximação”. Então o melhor é dizer que
Resposta
Exercício Resolvido #2
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 49-1.15.
A temperatura do ferro derretido pode ser estimada pela lei de Wien. Se o ponto de fusão do ferro é 1540°C, qual será o comprimento de onda (em nanômetros) que corresponde à intensidade máxima da radiação quando uma peça de ferro funde?
Passo 1
Deu a temperatura e pediu o comprimento de onda que corresponde à intensidade máxima de radiação.
Não tem erro: lei de Wien.
Ah, a gente não pode esquecer de passar a temperatura pra Kelvin hein!!!
Passo 2
Pela lei de Wien:
Para a temperatura:
Então:
Resposta
Exercício Resolvido #3
UFRJ – Lista de Exercícios de Química Geral. Professor Eon. Ex. 4.
Um laser produz uma radiação de comprimento de onda = 633 nm em pulsos de duração 1,3.10-9 s. Se o laser produz 0,376 J de energia por pulso, quantos fótons são produzidos em cada pulso? Calcule a potência do laser por pulso.
Passo 1
Calma aí. Ele tá tentando te confundir mas é só fazer uma coisa de cada vez que vai dar tudo certo!
Primeiro a gente vai usar aquele comprimento de onda pra descobrir a energia do fóton associado a ele. Pra isso, a gente vai ter que transformar de comprimento de onda pra frequência usando a velocidade da luzm/s.
Aí a gente vai saber qual é a energia de um fóton e descobrir quantos fótons são precisos pra ter aquela energia que o enunciado deu (0,376 J), fazendo uma regra de três amiga.
E por último, usamos o tempo dado pra descobrir a potência. Ou seja, quanta energia o laser produz por segundo.
Beleza? Bora lá.
Passo 2
A energia do fóton é dada por:
E os dados que temos são:
Calculando:
por fóton
Passo 3
Então já sabemos que cada fóton de comprimento de onda 633 nm tem 3,14.10-19 J de energia.
O enunciado nos diz que um pulso produz 0,376 J de energia. Vamos ver a quantos fótons essa energia corresponde:
fótons
Então cada pulso produz 1,2.1018 fótons.
E podemos, ainda, calcular quantos fótons o laser produz por segundo.
E sabemos que o laser produz 9,23.1026 fótons por segundo.
Passo 4
Para o cálculo da potência:
é o trabalho, ou seja, a energia transferida. Que no caso do laser é de 0,376 J.
Já é o tempo, dado como 1,3.10-9 s.
DÚVIDA: a potência é isso ou o que foi calculado no passo 3? “fótons/segundo”?
Resposta
fótons por pulso.
.
Exercício Resolvido #4
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 10-exemplo 1.4.
Qual é (a) a energia de um fóton de luz azul de frequência 6,4.1014 Hz; (b) a energia por mol de fótons da mesma frequência?
Passo 1
O item (a) o enunciado nos dá a frequência e pede a energia. Então só precisamos aplicar a fórmula:
Já no item (b), sabendo a energia de um fóton nessa frequência (calculado no item a), vamos calcular a energia associada a um mol de fótons, ou seja, 6,022.10²³ fótons, por regra de três.
Passo 2
Bora lá:
a)
E a energia de um fóton de luz azul na frequência dada é 4,24.10-19 J.
Passo 3
b) A gente sabe a energia de um fóton naquela frequência e queremos a energia de um mol de fótons:
J
Resposta
Exercício Resolvido #5
UFRRJ – Lista de Exercícios de Química Geral. Estrutura Atômica. Ex 1.14.
A cor azul do céu se deve ao espalhamento da luz do sol por um dos componentes do ar ou O2. A luz azul tem frequência de cerca de 7,2.1014 Hz. (a) Calcule o comprimento de onda (em nm) associado com esta radiação. (b) Calcule a energia (em J) de um único fóton associado a essa frequência.
Passo 1
No item (a) basta utilizar e a relação pra determinar o comprimento de onda da radiação.
E no item (b), a gente joga a frequência e a constante de Planck na fórmula “” e calcula a energia do fóton.
Partiu?
Passo 2
a)
Passo 3
b)
E a energia de um fóton de luz azul na frequência dada é 4,77.10-19 J.
Resposta
Exercício Resolvido #6
UFRRJ – Lista de Exercícios de Química Geral. Estrutura Atômica. Ex 1.16.
Calcule a diferença de energia (em J) entre um fóton com e um fóton com .
Passo 1
A gente sabe que a energia do fóton é dada por:
E o enunciado nos dá dois comprimentos de onda. A gente vai ter que descobrir a frequência dessas radiações pra calcular a energia de cada um dos fótons e comparar.
Bora lá.
Passo 2
Vamos chamar os comprimento de onda de e pra evitar confusão.
e
Passo 3
A gente pode calcular a energia de cada fóton e depois fazer a diferença entre elas. Mas vamos fazer direto a diferença, pra ter menos conta ok?
Então a diferença de energia entre um fóton com e um fóton com é igual a 1,58.10-19 J.
Resposta
Exercício Resolvido #7
UFRRJ – Lista de Exercícios de Química Geral. Estrutura Atômica. Ex 1.17.
A retina do olho humano pode detectar luz quando a energia radiante incidente sobre ela é de pelo menos 4,0.1011 J. Quantos fótons luz de 585 nm esta energia corresponde?
Passo 1
Primeiro vamos ter que calcular a energia de um fóton daquele comprimento de onda:
Então:
E depois ver a quantos fótons a energia dada () corresponde, através de uma regra de três.
Passo 2
Calculando:
Então é a energia de um fóton de 585 nm.
Passo 3
Agora vamos fazer uma regra de três pra determinar a quantos fótons corresponde a energia dada.
Então é preciso 1,18.1030 fótons de 585 nm pra atingir a energia necessária pra luz ser detectada pela retina humana.
Resposta
1,18.1030 fótons.
Exercício Resolvido #8
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 49-1.14.
Examine as seguintes informações sobre a radiação eletromagnética e decida se elas são verdadeiras ou falsas. Se forem falsas, corrija-as.
- Fótóns de radiação ultravioleta tem menos energia do que fótons de radiação infravermelha.
- A energia cinética de um elétron emitido por uma superfície metálica irradiada com luz ultravioleta é independente da frequência da radiação.
- A energia de um fóton é inversamente proporcional ao comprimento de onda da radiação.
Passo 1
(a) Fótóns de radiação ultravioleta tem menos energia do que fótons de radiação infravermelha?
Vamos dar uma olhada no espectro das radiações eletromagnéticas?
Tá vendo como o comprimento de onda cresce da esquerda para a direita enquanto frequência e energia crescem da direita para a esquerda?
Então fótons de radiação ultravioleta tem mais energia do que fótons de radiação infravermelha. E a afirmativa (a) está errada.
Você também pode pensar em termos de “” e usando uma frequência da região do ultravioleta e outra da região do infravermelho vai chegar na mesma conclusão.
Atenção! Às vezes o espectro aparece ao contrário do nosso. Ou seja, ali nos tipos de radiação, ondas de rádio vem primeiro, depois micro-ondas, infravermelho, etc... Então não basta decorar “tal coisa cresce da esquerda para a direita”.
Você pode pensar, por exemplo, que a gente usar protetor solar pra se proteger dos raios ultravioleta do Sol, mas todo mundo fica exposto ao micro-ondas ou às ondas de rádio. Isso quer dizer que os raios ultravioletas são mais energéticos (e por isso mais perigosos/danosos) que as micro-onas ou as ondas de rádio.
Passo 2
(b) A energia cinética de um elétron emitido por uma superfície metálica irradiada com luz ultravioleta é independente da frequência da radiação?
A gente viu que a energia cinética do elétron emitido pela superfície metálica é tipo a energia que sobrou depois que a gente deu o suficiente pra “soltar” ele do metal.
A energia que a gente “dá” é a energia do fóton () e a energia gasta pra soltar é a função trabalho do metal ().
Então a energia cinética de um elétron emitido ficou igual a:
E como aquele aparece ali, a energia cinética depende sim da frequência da radiação incidida. A afirmativa (b) também está errada.
Atenção! Se a afirmativa dissesse “comprimento de onda” ao invés de frequência? Também estaria errada! Embora o não apareça ali, ele está “implícito”, uma vez que e estão “amarrados” (um depende do outro).
Passo 3
(c) A energia de um fóton é inversamente proporcional ao comprimento de onda da radiação?
A energia do fóton é dada por:
E pra colocar em função do comprimento de onda:
E, finalmente, temos uma alternativa verdadeira. De fato a energia do fóton é inversamente proporcional ao comprimento de onda da radiação.
Resposta
(a) Falsa. Fótons de radiação ultravioleta tem mais energia do que fótons de radiação infravermelha.
(b) Falsa. A energia cinética de um elétron emitido por uma superfície metálica irradiada com luz ultravioleta é dependente da frequência da radiação.
(c) Verdadeira.
Exercício Resolvido #9
UFMG – Lista I de Exercícios de Química Geral. Questão 1.
O molibdênio metálico tem de absorver radiação com frequência mínima de 1,09.1015 s-1 antes que ele emita um elétron de sua superfície via efeito fotoelétrico.
- Calcule a energia mínima para retirar 1 mol de elétrons de uma placa de molibdênio metálico.
- Calcule o comprimento de onda associado a radiação. Em que região do espectro eletromagnética esta radiação é encontrada?
Passo 1
a) O enunciado nos dá:
Dizendo que essa é a radiação com energia necessária para liberar um elétron.
Vamos calcular a quanto de energia essa radiação corresponde e, em seguida, descobrir quanto de energia precisamos para liberar 1 mol de elétrons, aplicando uma regra de três.
Passo 2
Para calcular a energia associada à radiação usamos:
Então 7,22.10-19 J é a energia necessária para retirar 1 elétron.
Lembrando que 1 mol de elétrons corresponde a 6,022.1023 elétrons, aplicamos a regra de três:
Então precisamos de, no mínimo, 4,35.105 J para retirar um mol de elétrons de uma placa de molibdênio.
Passo 3
b) Para calcular o comprimento de onda associado a uma radiação de , precisamos aplicar:
E olhando no espectro você pode conferir que esse comprimento de onda corresponde a faixa do ultravioleta. :)
Resposta
a) kJ/mol de elétrons
b) nm. Ultravioleta.
Exercício Resolvido #10
UFRRJ – Lista de Exercícios de Química Geral. Estrutura Atômica. Ex 1.19. Modificada.
Qual a energia cinética dos elétrons ejetados se uma luz de frequência 2,0.1015 s-1 é usada para irradiar o magnésio metálico?
Dado: função trabalho do magnésio: 3,68 eV.
Passo 1
A energia cinética de elétrons ejetados é dada por:
E a gente tem que:
Então a primeira coisa que precisamos fazer é converter a função trabalho para Joules (ou a constante de Planck para eV).
1 eV corresponde a 1,602.10-19 J.
Passo 2
Todo mundo em suas devidas unidades! Só aplicar a fórmula sem medo de ser feliz.
E a energia cinética dos elétrons ejetados é igual a 7,36.10-19 J.
Resposta
.
Exercício Resolvido #11
UFRRJ – Lista de Exercícios de Química Geral. Estrutura Atômica. Ex 1.36.
Consome-se 208,4 kJ para remover um mol de elétrons de átomos na superfície do rubídio metálico. Se o Rb é irradiado com luz de comprimento de onda 254 nm, qual a energia cinética máxima que os elétons ejetados devem ter?
Passo 1
A função trabalho é a energia necessária para remover um elétron de uma superfície metálica.
Se 208,4 kJ são necessários para remover um mol de elétrons, quantos J são necessários para remover um único elétron (função trabalho)?
Então a energia necessária para remover um único elétron de uma superfície de rubídio e dada por:
Passo 2
A energia cinética de elétrons ejetados é dada por:
E a gente tem que:
Então só precisamos aplicar a fórmula, ok?
Passo 3
Vamos lá:
A energia cinética máxima que os elétrons deve ter é de 4,36.10-19 J.
Mas por que máxima? Porque utilizando a nossa fórmula de energia cinética a gente considera que toda energia do fóton não gasta para “soltar o elétron” foi convertida em energia cinética.
Então essa é a energia cinética máxima que os elétrons podem apresentar, numa situação ideal onde não ocorre perda de energia!
Flw.
Resposta
.
Exercício Resolvido #12
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 11-exemplo 1.5.
A velocidade de um elétron emitido pela superfície de uma amostra de potássio pela ação de um fóton é 668 km.s-1.
- Qual é a energia cinética do elétron ejetado?
- Qual é o comprimento de onda da radiação que provocou a fotoejeção do elétron?
- Qual é o comprimento de onda mais longo de radiação eletromagnética capaz de ejetar elétrons do potássio.
A função de trabalho do potássio é 2,29 eV.
Passo 1
a) Aqui ele dá a velocidade do elétron e pede a energia cinética. Então a gente aplica a fórmula mais “ordinária” da energia cinética:
Mas precisamos ter a massa do elétron, certo?
E é bom passar a velocidade pra unidades SI, que a nossa energia já fica bonitinha em joules.
E calcula a energia cinética:
Passo 2
b) Pra descobrir o comprimento de onda que provocou a ejeção do elétron, a gente vai aplicar a outra fórmula da energia cinética:
Sendo que a gente já sabe:
E a função trabalho é dada no final do enunciado:
Mas vamos passar pra joule, sabendo que 1 eV = 1,602.10-19 J.
E jogar tudo na fórmula pra descobrir a frequência (:
E o comprimento de onda:
Passo 3
c) Lembra que quanto maior o comprimento de onda, menor a energia da radiação?
Pois bem, quando o enunciado pergunta “qual o comprimento de onda mais longo” que é capaz de ejetar um elétron, ele tá pergutando qual o comprimento de onda quando a gente gasta o mínimo de energia possível para arrancar o elétron.
E quando a gente gasta o mínimo de energia pra arrancar o elétron?
Quando a energia gasta é exatamente a função trabalho . Ou seja, não “sobra” nada pra energia cinética.
Nessa situação:
Já temos e a constante de Planck. Então é só calcular a frequência e depois o comprimento de onda correspondente.
Resposta
a)
b)
c)