Séries Espectrais
Produzido por Marcelo BrillantinoTeoria
E aí?! Bora aprender sobre as séries espectrais?
Bem vindo ao RespondeAí! Aqui vamos falar sobre as séries espectrais. Essa é só uma partezinha de um assunto muito maior: Modelos Nucleares. Esse tema que vamos tratar hoje está muito relacionado com radiação e espectros atômicos.
Se você chegou aqui meio perdido, da uma conferida aqui nos conceitos de espectro de emissão, espectro de absorção, modelo de Bohr e depois volta aqui 😉
Agora vamos ao que interessa, vamos entender o que são séries espectrais!?
Pra começar vamos observar o espectro do hidrogênio, ok?

Cada uma dessas quatro linhas coloridas desse espectro representa um ou alguns életrons que saltou para um nível mais interno e liberou luz.
É exatamente isso que descreve o modelo de Bohr!
Ele diz que cada comprimento de onda presente no espectro atômico de emissão representa uma radiação emitida por um elétron ao saltar de um nível mas externo para um nível mais interno da eletrosfera, e dessa forma temos essas linhas da nossa fotinha!
Ou seja, cada transição eletrônica resulta na formação em uma linha espectral!
É exatamente aí que entram as séries espectrais! Vem comigo!
Será que existe uma forma de saber de qual nível eletrônico o elétron saltou e em qual nível ele foi parar?
-SIIIIM!!
A partir da observação espectro de absorção do hidrogênio podemos determinar o caminho do elétron!
-Mas como?
Vamos chamar os níveis da eletrosfera de
Se
Conhecendo os comprimentos de onda presentes no espectro do hidrogênio, por exemplo, é possível determinar entre quais níveis
Podemos usar as séries de linha de Rydberg, Lyman, Balmer, Paschen, entre outros, dependendo da situação.
Principais Séries Espectrais
A série mais geral é a série de linha de Rydberg:
Onde:
é a constante de Rydberg, de valor é o comprimento de onda. - e são inteiros que podem assumir qualquer valor
, contando que seja sempre maior que .
Dessa forma, com o comprimento de onda e o valor de
Para os casos em que
Com
A série de Lyman: nos permite saber, conhecendo o comprimento de onda, para qual nível o nosso elétron saltou.
Já para
Onde
Lembrando que cada valor de
Na figura abaixo temos uma tabela com as diferentes séries de linha, em quais condições se aplicam e suas regiões do espectro.
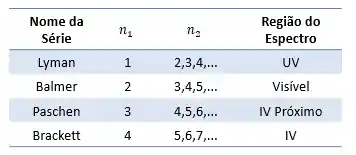
ATENÇÃO! As séries espectrais da tabela acima funcionam apenas para o átomo de hidrogênio!
Principais Séries Espectrais
Exercícios Resolvidos
Exercício Resolvido #1
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 7-exemplo 1.2. Modificado.
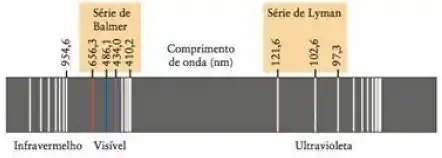
Calcule o comprimento de onda da radiação emitida por um átomo de hidrogênio para e . Identifique a linha espectral no espectro do hidrogênio abaixo.
Passo 1
Se ele dá os valores de e e pede o comprimento de onda, vamos usar essa equação aqui:
Como , a gente usa a série de Balmer. Que é a mesma coisa!
Agora a gente substitui o cm-1 e e calcula o
Passo 2
Bora lá:
Passo 3
Pra identificar a linha do espectro a gente procura uma linha que esteja nesse comprimento de onda.
Aqui, o comprimento de onda calculado se refere à linha vermelha do espectro.
Resposta
.
Linha vermelha.
Exercício Resolvido #2
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 49-1.7. Modificado.
- Use a fórmula de Rydberg para o átomo de hidrogênio e calcule o comprimento de onda da transição entre e .
- Qual é o nome dado à série espectroscópica a que esta linhda pertence?
- Determine a região do espectro na qual a transição é observada. Se a transição ocorre na região visível do espectro, que cor é emitida?
Passo 1
a) A primeira coisa é determinar quem é o e quem é o . Eaí?
A única restrição é que > . Se você não lembrar disso a sua resposta vai dar um número negativo e você vai ter que trocar os e refazer a conta. Nada muito grave, mas o tempo perdido pode ser precioso durante a prova certo?
Sendo assim: e .
Passo 2
Agora joga esses valores de na fórmula, substitui cm-1 e calcula o .
Passo 3
b) Dependendo de a série recebe um nome específico.
Para , a gente tem a Série de Balmer.
Passo 4
c) No nosso espectro, os comprimentos de onda estão mostrados em metros.
Em metros, a nossa resposta fica m, entre e . Olhando no nosso espectro das radiações eletromagnéticas, isso pode corresponder ou não à luz visível.
Como a luz visível vai de 450 nm à 750 nm, o comprimento de onda que calculamos pertence, sim, à luz visível. E fica na região do azul.
Resposta
- .
- Série de Balmer.
- Região do visível. Cor azul.
Exercício Resolvido #3
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 49-1.9. Modificado.
No espectro do átomo de hidrogênio, muitas linhas são classificadas como pertencendo a uma série (por exemplo, série de Balmer, série de Lyman, série de Paschen). O que as linhas de uma série têm em comum que torna lógico juntá-las em um grupo?
Passo 1
Como a gente comentou, a única coisa que determina a qual série uma linha espectral pertence é o valor de , isso é, o menor nível envolvido no pulo do elétron.
Quando a gente fixa o valor de , indiretamente, a gente acaba fixando em que região do espectro os valore de calculados vão ficar.
Assim, linhas da mesma série tem em comum o e a região do espectro ao qual as linhas pertencem.
Obs: se falamos do espectro de emissão, é o nível final do elétron, depois do pulo. Se falamos de um espectro de absorção, é o estado inicial do elétron. Assim será sempre menor que .
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
UFRJ – Lista de Química Geral. Espectros Atômicos.
Calcule o comprimento da terceira linha de Brackett para o hidrogênio.
Passo 1
Primeiro a gente precisa lembrar quem são os da série de Brackett.
Pode colar lá na teoria vai:
Passo 2
Aí a gente vai ter que decidir qual é a terceira linha.
Tecnicamente, olhando para o espectro, você pode começar a contar as linhas da direita para a esquerda ou da esquerda para a direita.
No entanto, pensando nos valores de .. eles vão de ao infinito.
Não dá pra saber qual é o terceiro número antes do infinito. Então a terceira linha de Brackett só pode ser aquela de .
Passo 3
Então: e .
Agora joga esses valores de na fórmula, substitui e calcula o .
E você ainda pode dar um confere pra ver em que região do espectro essa linha está:
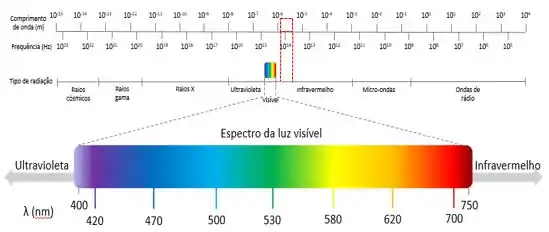
Beleza, infravermelho como o esperado!
Resposta
Exercício Resolvido #5
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 49-1.10.
No espectro do átomo de hidrogênio, observa-se um linha violeta em 434 nm. Determine os níveis de energia inicial e final da emissão de energia que corresponde a essa linha espectral.
Passo 1
Aqui, pela série de Rydberg, a gente vai ter que usar o comprimento de onda dado pra determinar os valores de e .
Pode parecer que a gente só tem o valor de , mas na verdade, sabendo a região do espectro que esse comprimento de onda está, a gente sabe também o !!!
Como a luz visível vai de 400 nm a 750 nm, nm cai no visível. Pela tabelinha que mostra os valores de para cada série, linhas no visível tem e correpondem à série de Balmer!
Passo 2
Agora joga esses valores de e na fórmula, substitui m-1 e calcula o .
A escolha da unidade do é puramente pessoal, ok? Só não pode esquecer de trabalhar com o na mesma dimensão.
Passo 3
Como estamos falando de um espectro de emissão, o elétron está pulando de um nível mais externo para um mais interno. Assim, o nível inicial é e o nível final é .
Resposta
(final) e (inicial).
Exercício Resolvido #6
UFMG – Lista de Química Geral. Estrutura Eletrônica. Modificada
Considere o átomo de hidrogênio no estado excitado, com um elétron no orbital 5p.
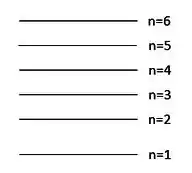
No diagrama abaixo, represente todas as transições de emissão possíveis para esse elétron, considerando apenas a série de Balmer. Calcule o comprimento de onda da radiação emitida de menor energia.
Passo 1
Fica calmo. Essa parada de 5p parece estranha mas, nesse momento, a única coisa que você tem que saber é que se o orbital é 5p, .
Como o enunciado deixa claro que só quer saber das transições que se enquadram na série de Balmer, a gente sabe que o do elétron é . Nesse caso, esse será o nível do elétron depois do salto (por se tratar de um espetro de emissão e ser o menor nível envolvido).
Aí a gente pode pensar que a única transição de emissão possível vai ser o elétron pulando de para . Mas isso não é verdade.
O elétron no nível 5 pode pular pro nível 2. Mas ele também pode pular pro nível 4 e depois ir pro nível 2 (em dois pulos sucessivos), ou pro nível 3 e depois ir por nível 2. E todos os pulos com vão aparecer no espectro como uma linha da série de Balmer, certo?
Passo 2
Então, a representação de todas as transições de emissão pertencentes à série de Balmer fica assim:
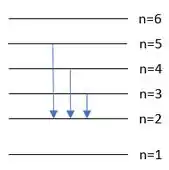
Passo 3
Pra calcular o comprimento de onda da radiação de menor energia a gente precisa, primeiro, decidir qual das transições envolve uma menor diferença de energia.
Eaí?
A transição que envolve menor diferença de energia é, justamente, a que envolve menor diferença entre os níveis.
Então: e .
Agora joga esses valores de na fórmula, substitui e calcula o .
Resposta
Exercício Resolvido #7
USP/IQSC – Lista de Química Geral. Estrutura Atômica.
Usando a equação de Rydberg, calcule para 3 algarismos significativos o comprimento de onda das linhas nas séries de Lyman () para até . À medida que se aproxima do infinito, de que valor-limite o comprimento de onda se aproxima?
Passo 1
O enunciado já nos diz que para a série de Lyman e pede pra gente calcular diversos valores de variando .
Então, mãos à obra que temos bastante conta pela frente.
Passo 2
Para :
Passo 3
Para :
Passo 4
Para :
Passo 5
Para :
Passo 6
Para :
Passo 7
Para :
Passo 8
Para :
Passo 9
O que que acontece quando ?
Resposta
Para ,
Para ,
Para ,
Para ,
Para ,
Para ,
Para ,
Para ,
Exercício Resolvido #8
UFRRJ – Lista de Exercícios de química Geral. Estrutura Atômica.
Quando um elétron do átomo hélio é removido, forma-se a espécie He+. O íon He+ tem apenas um elétron e é considerado um átomo hidrogenóide. Calcule os comprimentos de onda em ordem crescente das primeirs quatro transições na série de Balmer para o íon He+. Compare esse resultado com os observados para o átomo de H. (Constante de Rydberg para o He, ).
Passo 1
O átomo de hélio é um cara com 2 elétrons. No cátion He+, a gente tem só um elétron... como no hidrogênio. Então as séries do He+ são beeeem parecidas com as do H, que a gente já tá acostumado a fazer. A única diferença é o valor da constante, que é dado no enunciado.
Sem esquecer que pra série de Balmer,
E as primeiras quatro transições são aquelas de e .
Então não tem segredo, só conta.
Passo 2
Para :
Passo 3
Para :
Passo 4
Para :
Passo 5
Para :
Passo 6
Em relação aos valores de que seriam calculados para o H dados os mesmos e , os valores de que encontramos para o He+ são bastante diferentes.
As linhas da série de Balmer para o hidrogênio ficam na região do visível, enquanto para o He+, todos os comprimentos de onda que calculamos estão no ultravioleta.
Resposta
Para ,
Para ,
Para ,
Para ,
Exercício Resolvido #9
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 49-1.11.
Os níveis de energia dos íons hidrogenóides, com um elétron e número atômico , diferem dos níveis de energia do hidrogênio por um fator igual a . Prediga o comprimento de onda da transição do He+.
Passo 1
Esse exercício é um pouco diferente do que vimos até agora.
Tudo que a gente tem visto em séries é aplicado ao hidrogênio, e agora ele pede pra gente aplicar isso pra um átomo hidrogenóide (mesmo número de elétrons que o hidrogênio, mas número atômico diferente).
Basicamente você precisa fazer o que sempre fazemos, mas multiplicando aquele fator pra passar pro hidrogenóide.
Lembrando que é o número atômico, ou seja, o número de prótons. Então:
E uma transição do tipo tem:
Por quê?
Porque é uma transição do nível 2 para o nível 1 e a gente sempre usa o maior como .
Passo 2
Pro hidrogênio:
Agora ele diz que o fator altera a ENERGIA dos níveis, e não os comprimentos de onda diretamente. Então a gente tem que transformar a fórmula acima pra energia.
E a gente usa essa relação daqui:
Onde é a energia, é a constante de Planck (6,6.10-34 J.s) e a frequência.
Como:
Então:
E a gente pode substituir isso na nossa famigerada série de Rydberg:
Sendo que, para a energia do He+ a gente precisa aplicar o fator :
Passo 3
Substituindo o que temos:
Chegamos a:
Passo 4
Mas o exercício nos pede mesmo o comprimento de onda referente a transição, então vamos aplicar de novo a relação:
Resposta
Exercício Resolvido #10
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 49-1.12. Modificado.
Possivelmente muito mais difícil do que o necessário. “assusta mais do que ajuda”
Alguns lasers funcionam pela excitação de átomos de um elemento e colisão posterior entre os átomo excitados e os átomos de outro elemento com transferência de energia. A transferência é mais eficiente quando a separação dos níveis de energia é a mesma nas duas espécies. Dado que:
Existe alguma transição do He+ (incluindo transições de seus estados excitados) que poderia ser excitada pela colisão com um átomo de hidrogênio de configuração 2s¹?
Dado:
Passo 1
Vamos tentar entender o que o exercício está pedindo.
Basicamente ele quer excitar o elétron do átomo de hidrogênio até (configuração 2s¹) e colidir esse átomo excitado com um átomo de He+. Quando isso acontecer, o elétron excitado do átomo de hidrogênio pula para um nível mais interno (), cedendo energia para excitar o elétron do átomo de He+.
Isso só será possível se a transição do para o do hidrogênio tiver energia próxima da enegria da transição que vai occorer no He+.
Passo 2
Para a transição do hidrogênio:
E agora precisamos tentar encontrar uma transição no átomo de He+ que ocorra com essa mesma energia, para que a colisão seja efetiva (excite um átomo do He+).
Passo 3
A energia da transição do He+ deve ser:
Então o comprimento de onda que corresponde à transição será:
Passo 4
Precisamos, agora, usar a série de Rydberg fornecida no enunciado para verificar se existem dois números inteiros ( e ) capazes de gerar o comprimento de onda calculado.
Seja :
E a partir daqui é na tentativa e erro mesmo.
Se você substituir os por valores de 1 a 4 já vai dar pra ver que:
Ou seja:
Passo 5
Logo:
Existe alguma transição do He+ (incluindo transições de seus estados excitados) que poderia ser excitada pela colisão com um átomo de hidrogênio de configuração 2s¹?
Sim. Vimos que a energia liberada pelo elétron do hidrogênio ao pular do nível 2 para o nível 1 é equivalente à energia que um elétron do He+ precisa absorver para pular do nível 2 para o nível 4.
Resposta
Sim, a transição do nível 2 para o nível 4 da eletrosfera.