Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Princípio da Exclusão de Pauli

Ver Todos os Exercícios

Teoria

“Em um átomo, dois elétrons quaisquer nunca poderão ter o mesmo conjunto de
números quânticos , ou seja, os dois elétrons nunca estarão no
mesmo estado quântico”

Esse é o enunciado do que a gente conhece por Princípio da Exclusão de Pauli feito por Wolfgang Pauli em 1925!

Essa imagem resume bastante como funciona o Princípio de Pauli:

Princípio de Pauli
Princípio de Pauli

- Beleza, mas na prática, o que isso significa? 😵‍💫

Na prática isso significa que dois elétrons nunca podem “ter o mesmo endereço” e ele vai dizer a maneira certa de preencher o diagrama de caixas!

Se por acaso a gente colocar dois elétrons no mesmo orbital com o mesmo spin, eles terão os quatro números quânticos idênticos... E o foi exatamente o que Pauli disse que não pode!

Números Quânticos

Precisamos ter em mente que um elétron pode ser descrito por quatro números quânticos, que funcionam como o “endereço do elétron”

  • Número quântico principal ()
    • Ele indica em qual camada da eletrosfera o elétron se encontra

  • Número quântico azimutal ()
    • Ele indica em qual camada da eletrosfera o elétron se encontra

  • Número quântico magnético
    • Ele nos informa como o orbital está orientado no espaço. Ele pode assumir valores inteiros entre e .

      Por exemplo, se , então

  • Número quântico de spin
    • Se refere ao movimento do elétron em torno de seu próprio eixo. O elétron pode girar no sentido anti-horário (representado por  ) ou no sentido horário (representado por 
      ), assim o número quântico   pode assumir dois valores:

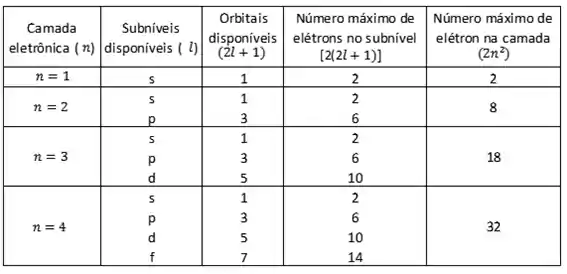
Sabendo que o número máximo de elétrons por orbital é podemos saber o número máximo de elétrons por subnível ou nível, olha só essa tabelinha:

Números quânticos
Números quânticos

Regra de Hund

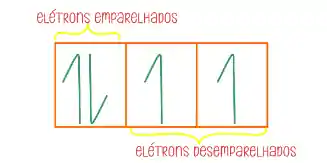
Para entender a regra de Hund você precisa saber que elétron desemparelhado é quando a gente tem um elétron sozinho no orbital. Já elétrons emparelhados é quando eles estão em par no orbital.

Assim:

Elétrons emparelhados e desemparelhados
Elétrons emparelhados e desemparelhados

Segundo Hund, quando a gente vai distribuir os elétrons nos orbitais, a gente deve priorizar elétrons desemparelhados e com o mesmo spin. Essa é a configuração eletrônica menos energética e, portanto, mais estável para um átomo.

Isso acontece porque quando a gente coloca os elétrons emparelhados, rola uma repulsão entre eles e a energia do átomo aumenta. Então elétron sozinho no orbital diminui a energia do sistema, beleza?

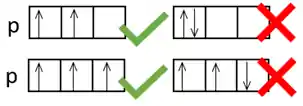
Olha o esqueminha pra não esquecer, para um sistema no estado fundamental ou seja mais baixa energia possível:

Regra de Hund
Regra de Hund

Fechou?

Agora eu vou deixar um resuminho em vídeo, com tudo o que você precisa saber sobre o princípio de Pauli 👇👇👇

Agora vamos praticar com exercícios!

Números Quânticos

Regra de Hund

Exercícios Resolvidos

Exercício Resolvido #1

Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 35-Teste 1.11.

  1. Prediga a configuração do átomo de magnésio no estado fundamental.
  2. Prediga a configuração do átomo de alumínio no estado fundamental.

Passo 1

Vamos dar uma olhada no Diagrama de Pauling aí:

E agora vamos ver na tabela periódica o número atômico do magnésio e do alumínio pra fazer a distribuição eletrônica deles:

M g 12 24         e       A l 13 27

Beleza.

Agora a gente vai pegar aquele numerozinho de baixo (que na tabela periódica aparece em cima).

Ele é o número de prótons do átomo, mas é também o número de elétrons de um átomo de carga neutra.

E vamos distribuir os elétrons em ordem e energia, do mais baixo pro mais alto, conforme o diagrama.

Valeu?

Passo 2

  1. M g 12 24      

    2. O átomo de magnésio tem 12 elétrons.

    Pelo diagrama, a gente começa na primeira seta, que atravessa o 1s². Já foram 2 elétrons.

    Passa pra segunda seta, que atravessa o 2s². Mais 2 elétrons, foram 4.

    A terceira seta atravessa o 2p6 e o 3s². Mais 8 elétrons, foram 12. Acabou.

    Então a configuração do magnésio fica assim:

    M g : 12   1s² 2s² 2p6 3s²

    Mas também tem aquele jeito de representar, considerando a configuração eletrônica de um gás nobre. Nesse caso:

    M g : 12   [Ne] 3s²

    Porque o neônio é o último gás nobre antes do Mg na tabela periódica. E a configuração eletrônico do neônio é, justamente, 1s² 2s² 2p6.

    Passo 3

  2. A l 13 27

Agora é a vez da configuração eletrônico do alumínio.

Ele tem um elétron a mais que o magnésio. Então a configuração eletrônica dele é igual a do magnésio mais um elétron.

Vamos seguir o mesmo raciocício de antes:

A gente começa na primeira seta, que atravessa o 1s². Já foram 2 elétrons.

Passa pra segunda seta, que atravessa o 2s². Mais 2 elétrons, foram 4.

A terceira seta atravessa o 2p6 e o 3s². Mais 8 elétrons, foram 12.

Passando pra quarta seta, a gente vê que ele cruza primeiro o 3p6. Mas se a gente fazer isso vai somar 6 elétrons na nossa distribuição, fechando 18. E o alumínio só tem 13. Então ao invés de incluir 3p6, a gente coloca 3p1.

Bora ver como ficou:

A l : 13   1s² 2s² 2p6 3s² 3p1

Ou, levando em consideração a distribuição do último gás nobre antes do alumínio na tabela periódica, fica assim:

A l : 13   [Ne] 3s² 3p1

Prontinho!

Resposta

  1. M g : 12   1s² 2s² 2p6 3s² ou [Ne] 3s²
  2. A l : 13   1s² 2s² 2p6 3s² 3p1 ou A l : 13   [Ne] 3s² 3p1

Exercício Resolvido #2

Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 51-1.57.

Quantos elétrons, no total, podem ocupar:

  1. Os orbitais 4p;
  2. Os orbitais 3d;
  3. O orbital 1s;
  4. Os orbitais 4f?

Passo 1

Pra resolver esse exercício, a gente pode simplesmente olhar o no diagrama de Pauling, porque aquele numerozinho lá de cima, é justamente o número máximo de elétrons suportado por cada orbital.

Mas a gente pode fazer melhor e tentar entender vai.. Olha as dicas:

O número de orbitais no subnível é dado por 2 l + 1 .

E cada orbital comporta, no máximo, 2 elétrons.

Então o número máximo de elétrons no subnível é 2 ( 2 l + 1 ) .

Vamos ver juntos cada caso.

Passo 2

  1. Para os orbitais 4p:

    2. Eles estão no 4° nível da eletrosfera e no subnível p, o que corresponde ao número quântico secundário l = 1 .

    O número de orbitais no subnível é dado por 2 l + 1 = 2.1 + 1 = 3 orbitais

    E cada orbital comporta, no máximo, 2 elétrons.

    Então o número máximo de elétrons no subnível é 2.3 = 6 elétrons.

    Passo 3

  2. Para os orbitais 3d:

    3. O número quântico secundário correspondente ao subnível d é o l = 2 .

    Então o número de orbitais 3d é: 2 l + 1 = 2.2 + 1 = 5 orbitais.

    Com 2 elétrons por orbital a gente vai ter, no máximo, 10 elétrons nos orbitais 3d.

    Passo 4

  3. Para o orbital 1s:

    4. O número quântico secundário correspondente ao subnível s é o l = 0 .

    Então o número de orbitais 1s é: 2 l + 1 = 2.0 + 1 = 1 orbitais.

    E com 2 elétrons por orbital a gente vai ter, no máximo, 2 elétrons no orbital 1s.

    Passo 5

  4. Para os orbitais 4f.

O número quântico secundário correspondente ao subnível f é o l = 3 .

Então o número de orbitais 4f é: 2 l + 1 = 2.3 + 1 = 7 orbitais.

Com 2 elétrons por orbital a gente vai ter, no máximo, 14 elétrons nos orbitais 4f.

Resposta

  1. 6 elétrons
  2. 10 elétrons
  3. 2 elétrons
  4. 14 elétrons

Exercício Resolvido #3

Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 51-1.58.

Quantos elétrons podem ocupar uma subcamada com l igual a:

  1. 0
  2. 1
  3. 2
  4. 3?

Passo 1

Pra resolver esse exercício, a gente pode ver qual a letra correponde a cada valor de l e simplesmente olhar o no diagrama de Pauling, porque aquele numerozinho lá de cima, é justamente o número máximo de elétrons suportado por cada subcamada.

Mas a gente pode pensar naquelas caixinhas que representam os orbitais de cada subcamada. Lembrando que:

  • O número de orbitais em cada subcamada é dado por 2 l + 1 .
  • Cada orbital comporta, no máximo, 2 elétrons.

Então o número máximo de elétrons na subcamada é 2 ( 2 l + 1 ) .

Vamos ver juntos cada caso.

Passo 2

  1. l = 0 :

    2. Corresponde à subcamada do tipo s.

    Olhando no diagrama, dá pra ver que subcamadas do tipo s aceitam no máximo 2 elétrons.

    Pelas nossas continhas:

    O numero de orbitais presentes em uma subcamada do tipo s é: 2.0 + 1 = 1 orbital.

    Que a gente representa por uma caixinha.

    Lembrando que cada caixinha pode ter no máximo 2 elétrons.

    Então 2 elétrons podem ocupar uma subcamada com l = 0 .

    Passo 3

  2. l = 1

    3. Corresponde à subcamada do tipo p.

    Olhando no diagrama, dá pra ver que subcamadas do tipo p aceitam no máximo 6 elétrons.

    Vamos ver se bate com as nossas contas:

    Número de orbitais: 2 l + 1 = 2.1 + 1 = 3 orbitais

    Número de elétrons máximos por orbital: 2 elétrons

    Número de elétrons na subcamada: 2.3 = 6 elétrons.

    Que no diagrama das caixinhas a gente representa assim:

    Passo 4

  3. l = 2

    4. Corresponde à subcamada do tipo d.

    Olhando no diagrama, dá pra ver que subcamadas do tipo d aceitam no máximo 10 elétrons.

    E pelas nossas contas:

    Número de orbitais: 2 l + 1 = 2.2 + 1 = 5 orbitais

    Número de elétrons máximos por orbital: 2 elétrons

    Número de elétrons na subcamada: 2.5 = 10   elétrons.

    Ufa! Deu o mesmo resultado! :p

    E no diagrama das caixinhas a gente representaria assim:

    Passo 5

  4. l = 3

Corresponde à subcamada do tipo f.

Olhando no diagrama, dá pra ver que subcamadas do tipo f aceitam no máximo 14 elétrons.

Vamos ver:

Número de orbitais: 2 l + 1 = 2.3 + 1 = 7 orbitais

Número de elétrons máximos por orbital: 2 elétrons

Número de elétrons na subcamada: 2.7 = 14   elétrons.

E no diagrama das caixinhas a gente representaria assim:

Resposta

  1. 2 elétrons
  2. 6 elétrons
  3. 10 elétrons
  4. 14 elétrons

Exercício Resolvido #4

Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 51-1.61.

Quantos elétrons podem ter os seguintes números quânticos:

  1. n = 2 ,     l = 1
  2. n = 4 ,     l = 2 ,     m l = - 2
  3. n = 2
  4. n = 3 ,     l = 2 ,     m l = + 1

Passo 1

Pra resolver esse exercício, vamos fazer umas contas bem básicas e desenhar os diagramas das caixinhas pra “enxergar” melhor o nosso resultado.

Lembrando que:

  • O número de orbitais em cada subcamada é dado por 2 l + 1 .
  • Cada orbital comporta, no máximo, 2 elétrons.

Então o número máximo de elétrons na subcamada é 2 ( 2 l + 1 ) .

Vamos ver juntos cada caso.

Passo 2

  1. n = 2 ,     l = 1

    2. Com l = 1 a gente tem orbitais do tipo p.

    Pra saber a quantidade de orbitais 2p que temos: 2 l + 1 = 2.1 + 1 = 3 orbitais

    O que significa três “caixinhas”. E dentro de cada caixinha/orbital, podemos colocar 2 elétrons

    Todos os elétrons que a gente representou aí tem n = 2 e l = 1 . Eles se diferenciam, portanto, pelos valores de m l e m s .

    Então 6 elétrons podem ter n = 2 e l = 1 .

    Passo 3

  2. n = 4 ,     l = 2 ,     m l = - 2

    3. Sabemos que dois elétrons não podem ter os 4 números quânticos em comum.

    O enunciado já determina 3 números quânticos, faltando apenas o m s , que pode assumir somente 2 valores: - 1 2   o u + 1 2 .

    Logo, apenas dois elétrons podem ter esses 3 números quânticos definidos. O elétron de spin ↑ e o elétron de spin ↓ .

    Vamos ver nas caixinhas:

    Orbitais com l = 2 são do tipo d. Para saber quantos orbitais do tipo d a gente tem:

    2 l + 1 = 2.2 + 1 = 5 orbitais.

    Cada caixinha/orbital representa um valor diferente de m l . Então nosso diagram fica assim:

    E os 2 elétrons que podem ter os 3 números quânticos definidos no enunciado estão destacados em vermelho.

    Passo 4

  3. n = 2

    4. Aqui a gente tá falando de toda a segunda camada.

    As subcamadas possíveis para uma camada são dadas por:

    l = 0 ,   1 ,   … ,   n - 1

    Ou seja, o máximo valor que l pode assumir dentro de uma camada n é n - 1 .

    Pra n = 2 , os valores possíveis de l são:

    l = 0 ,   1

    Então a segunda camada da eletrosfera pode ter subníveis do tipo s e do tipo p.

    Para o subnível 2s, o número de orbitais é: 2 l + 1 = 2.0 + 1 = 1 orbital.

    Para o subnível 2p, o número de orbitais é: 2 l + 1 = 2.1 + 1 = 3 orbitais.

    Então para n = 2 a gente tem 4 orbitais. Com 2 elétrons possíveis por orbital, a gente vai ter 8 elétrons no nível n = 2 .

    Passo 5

  4. n = 3 ,     l = 2 ,     m l = + 1

Mesma situação do item b, onde a gente já tem 3 números quânticos definidos, o que significa que estamos falando de um único orbital, no qual só cabem 2 elétrons, com spin opostos.

Vamos ver..

2 l + 1 = 5 orbitais

Resposta

  1. 6 elétrons
  2. 2 elétrons
  3. 8 elétrons
  4. 2 elétrons

Exercício Resolvido #5

UFS- Lista de Exercícios de Química Geral. Questão 13.

Os sete orbitais f podem ser, simplificadamente, representados conforme o esquema abaixo:

  1. Quantos elétrons cabem em cada orbital f?
  2. Quantos elétrons cabem no subnível f?

Passo 1

  1. Em cada orbital, independente se ele é do tipo s, p, d, f, g..., cabem apenas 2 elétrons, sempre de spin opostos ( ↑ e ↓ ).

    2. Passo 2

  2. Pelo esquema do enunciado, a gente vê que existem 7 orbitais. Se cada orbital pode conter 2 elétrons, o número total de elétrons comportados é 14 elétrons.

Assim:

Resposta

  1. 2 elétrons
  2. 14 elétrons

Exercício Resolvido #6

Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 51-1.63/1.64.

Quais das seguintes subcamadas não podem existir em um átomo?

  1. 2d
  2. 4d
  3. 4g
  4. 6f
  5. 4f
  6. 3f
  7. 5g
  8. 6h

Passo 1

A gente viu que os valores aceitos para o número quântico secundário são:

l = 0 ,   1 ,   2 ,   … ,   n - 1

Então vamos analisar quais alternativas do enunciado não respeitam essa regra:

O valor máximo permitido para l é n - 1 . Então, toda vez que isso não é respeitado, o subnível não existe.

Resposta

  1. 2d – não existe
  2. 4d – existe
  3. 4g – não existe
  4. 6f – existe
  5. 4f – existe
  6. 3f – não existe
  7. 5g – existe
  8. 6h – existe

Exercício Resolvido #7

UFRRJ – 1ª Lista de Exercícios de Química Geral. Estrutura Atômica. Questão 1.32.

A figura abaixo ilustra porções de diagrama de orbitais representando a configuração eletrônica de estado fundamental de certos elementos. Qual deles viola o princípio de exclusão de Pauli? Qual deles viola a regra de Hund?

Passo 1

Vamos relembrar essas regras aí:

Pela regra de Pauli, o número máximo de elétrons por orbital é 2. E eles tem que ter spin opostos, ou seja, um assim ↑ e outro assim ↓ .

Pela regra de Hund, ao completar um subnível com elétrons, só podemos colocar o segundo elétron em um orbital depois que todos os outros orbitais já tenham ao menos um elétron. Ou seja, a gente não pode ter um orbital com 2 elétrons se existe orbital vazio. Além disso, devemos colocar o máximo possível de elétrons com spin em comum.

Vamos dar uma olhada item por item:

Passo 2

  1. Pela regra de Hund até vai, mas colocar dois elétrons com o mesmo spin [ ↑ ↑ ] no mesmo orbital desrespeita o princípio de Pauli.

    2. Passo 3

  2. Pela regra de Hund, a gente deve colocar o número máximo de elétrons com o mesmo spin. Tipo, primeiro a gente coloca um elétron por orbital e todos com o mesmo spin, e depois coloca o resto, com o spin diferente.

    3. Vamos ver algumas formas de distribuir aqueles 4 elétrons sem desrespeitar Tio Hund:

    Já pelo princípio de Pauli tava tudo ok!

    Passo 4

  3. Hund e Pauli felizes! Primeiro colocou um elétron em cada orbital (todos com mesmo spin) e depois colocou um segundo elétron em um orbital, com spin diferente.

    4. Passo 5

  4. Hund mandou avisar que enquanto tiver orbital sem elétron, nenhum orbital pode ter dois elétrons.

    5. Já por Pauli, tava tudo tranquilo.

    Passo 6

  5. O problema é aquele quarto orbital com o elétron com spin pra baixo. Por Hund a gente deve priorizar o máximo de elétrons com o mesmo spin. Os esquemas aí embaixo são só exemplos de possibilidades que respeitam Hund e Pauli. Existem outras, ok?

    6. Passo 7

  6. Colocar dois elétrons com o mesmo spin no mesmo orbital é sacanagem né? Desrespeita o princípio da exclusão de Pauli! Aqueles dois elétrons tem os 4 números quânticos idênticos! Mr. Pauli mandou avisar que não pode!

Resposta

Violam o princípio da exclusão de Pauli: a, f.

Violam a regra de Hund: b, d, e.

Exercício Resolvido #8

UFRRJ – 1ª Lista de Exercícios de Química Geral. Estrutura Atômica. Questão 1.9.

Defina os termos diamagnético e paramagnético.

Passo 1

A gente chama um átomo (ou molécula) de diamagnético quando todos os seus elétrons estão emparelhados. Ou seja, todos os elétrons estão dispostos em pares nos seus respectivos orbitais.

Já átomos (ou moléculas) paramagnéticos, possuem elétrons desemparelhados. Ou seja, ao fazer a distribuição eletrônica deles, alguns elétrons ficam “sozinhos” nos orbitais.

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #9

UFS- Lista de Exercícios de Química Geral. Questão 11. Modificada.

Entre as configurações eletrônicas abaixo, todas representando átomos isolados ou monoatômicos. Encontre o número de elétrons desemparelhados de cada configuração e indique se os átomos são paramagnéticos ou diamagnéticos.

  1. 1s² 2s¹
  2. 1s² 2s² 2p¹
  3. 1s² 2s² 2p³
  4. 1s² 2s² 2p6
  5. 1s² 2s² 2p6 3s² 3p6 4s² 3d10

Passo 1

Vamos lembrar que elétrons desemparelhados são aqueles “sozinhos” no orbital, e não em par.

Pra ver se existem elétrons desemparelhados a gente só precisa estudar o último subnível da distribuição eletrônica, porque todos os demais estão completos, emparelhados.

Quanto à classificação: sempre que existirem elétrons desemparelhados, os átomos apresentam paramagnetismo. Se todos os elétrons estiverem emparelhados, diamagnetismo.

Bora lá:

Passo 2

a)

1 elétron desemparelhado. Paramagnético.

Passo 3

b)

1 elétron desemparelhado. Paramagnético.

Passo 4

c)

3 elétron desemparelhados. Paramagnético.

Passo 5

d)

0 elétron desemparelhados. Diamagnético.

Passo 6

e)

0 elétron desemparelhados. Diamagnético.

Resposta

  1. 1 elétron desemparelhado. Paramagnético.
  2. 1 elétron desemparelhado. Paramagnético.
  3. 3 elétrons desemparelhados. Paramagnético.
  4. 0 elétrons desemparelhados. Diamagnético.
  5. 0 elétrons desemparelhados. Diamagnético.

Exercício Resolvido #10

UFRRJ – 1ª Lista de Exercícios de Química Geral. Estrutura Atômica. Questão 1.46.

Um certo átomo de oxigênio tem configuração eletrônica 1s² 2s² 2px² 2py². Quantos elétrons desemparelhados estão presentes? Este estado é um estado excitado do átomo de oxigênio? Indo deste estado para o estado fundamental, ocorrerá absorção ou emissão de energia?

Passo 1

Primeiro vamos representar os orbitais desse oxigênio aí:

O que realmente nos interessa são os orbitais 2p, os mais energéticos.

Note que não existem elétrons desemparelhados. Todos estão em pares.

Pelas regras de Hund e Pauli, a distribuição eletrônica nos orbitais 2p deveria ser feita assim:

Segundo eles, a configuração acima representa um mínimo de energia, porque ao emparelhar elétrons, as forças de repulsão entre eles aumentam e o átomo passa para um nível energético maior.

Portanto, a configuração acima é a mais estável, mas não é a única possível.

A configuração do enunciado representa, portanto, um estado menor estável, sendo mais energético: um estado excitado!

Para sair do estado excitado e ir para o estado fundamental o elétron emite energia.

Resposta

Não existem elétrons desemparelhados.

É um estado excitado.

Emissão de energia.

Exercícios de Livros Relacionados

As seguintes configurações de camada de valência são possíveis para um átomo neutro. Que elemento e que configuração correspondem ao estado fundamental?
Para cada um dos seguintes átomos no estado fundamental, prediga o tipo de orbital (por exemplo, 1s, 2p, 3d, 4f, etc.) do qual um elétron poderia ser removido para torná-lo um íon +1:(a) Ge; (b) Mn; (
24. Use as configurações eletrônicas para sugerir uma razão por que ferro(II) é facilmente preparado a partir do ferro(II), mas a conversão do níquel(II) e cobalto(II) a níquel(III) e cobalto(III) são
O estado fundamental do O 2 possui dois elétrons π * desemparelhados com spins paralelos. Existem dois estados excitados de baixa energia. O estado A tem os dois elétrons π *com os spins antiparalelos
23. Use as configurações eletrônicas para explicar por que o ouro e a prata são mais reativos do que o cobre.