Números Quânticos e Funções de Onda
Produzido por Marcelo BrillantinoTeoria
Os orbitais e a equação de Schrödinger
Você se lembra que no modelo de Bohr, o elétron ficava girando na volta do núcleo, na eletrosfera, né? O lugar onde o elétron “habitava” era uma órbita.
Mas agora que descobrimos que o elétron tem um comportamento dual onda-partícula, a gente entende que ele não está “girando ao redor do núcleo”.
Agora, a gente não fala sobre “onde o elétron está”, mas sim onde a probabilidade de encontrar o elétron é máxima.
A máxima probabilidade de encontrar o elétron está no orbital.
Talvez ao falar de orbital, você já pense naqueles desenhos de orbitais s, p, d, etc. A gente vai chegar lá, mas é preciso de um pouco mais de teoria antes disso. Esses conceitos são bem importantes.
O orbital nada mais é do que uma função de onda que descreve o elétron.
Como assim?
Você sabe o que é uma função.
é uma função, é uma função, é uma função, também.
Uma função de onda é uma função capaz de descrever um sistema físico!
Partindo do estudo da física e com ferramentas de cálculo do satanás Schrödinger deduziu a equação abaixo:
Onde esse é chamado de hamiltoniano, (a letra grega psi) é a função de onda, e a energia do sistema.
As funções que obedecem essa equação aqui em cima são as funções de onda que podem descrever o estado do elétron 😊
Trabalhando a equação aí de cima, Schrödinger deduziu ainda a fórmula para o cálculo dos níveis de energia de um elétron como:
Onde é o número atômico do átomo, é a nossa velha conhecida constante de Planck ( J.s), é uma constante e um número que assume valores inteiros positivos.
E como a gente interpreta a equação de Schrödinger?
Bohr já tinha falado que a energia era quantizada, e que o elétron só poderia assumir valores discretos de energia. Mas ele não tinha provado. E Schrödinger provou!
A parte de cima da equação da energia é formada por constantes e a parcela de baixo só pode assumir determinados valores, logo, a própria energia só pode assumir determinados valores.
A gente costumava chamar esse que apareceu aí de camada da eletrosfera. Não é mentira. Só não pode pensar que camada é necessariamente uma divisão do espaço. Ela tá mais pra uma divisão de energia.
Elétrons com mesmo possuem a mesma energia e, portanto, estão no mesmo nível energético.
Orbitais de mesma energia são chamados orbitais degenerados. Em átomos não hidrogenóides (com mais de um elétron), isso não é bem assim. Orbitais com o mesmo podem ter energias diferentes. No hidrogênio e outros caras com um elétron só, quem tem o mesmo tem a mesma energia.
O sinal de menos na equação faz toda a diferença. Isso significa que quando o elétron está no átomo, a energia dele é menor do que quando está distante do núcleo, “solto”.
Além disso, quanto maior for o (mais prótons o átomo tiver), mais negativa será a energia do elétron. Ou seja, mais preso o elétron está ao núcleo.
Quando aumenta, a energia diminui em módulo, mas aumenta (porque é negativa). Ainda bem, porque a gente sabe que pra passar para um nível maior o elétron precisa absorver energia.
Schrödinger e os espectros de linhas
Aquela constante é calculada através de:
Onde é a massa do elétron e vale kg, é a carga do elétron e vale C, o é a constante de Planck mesmo e o é a constante de permissividade elétrica do vácuo, que vale .
Se você substituir todo mundo aí, vai encontrar .
Agora lembra como a gente calculava as séries de linha do hidrogênio? Era assim:
E pra transformar isso em energia:
Essa é a energia necessária pra pular de um nível para o outro. A energia de cada nível é dada por:
Hmm, ficou bem parecida com a equação de Schrödinger né? Na verdade, ficou igual! Porque
MAS ENTÃO O SCHRÖDINGER NÃO FEZ NADA DEMAIS NÉ????
Fez sim! As séries de linha e a fórmula de energia através delas eram frutos de observações experimentais, postulados... ninguém sabia porque que era assim. E Schrödinger PROVOU matematicamente.
Função de onda, probabilidade e densidade de probabilidade
Quando a gente tem uma equação que define bem direitinho a energia do elétron, quer dizer que a gente consegue calcular a energia cinética do elétron (e consequentemente sua velocidade) com uma precisão bem grande.
E pelo princípio da incerteza de Heisenberg, isso significa que a gente tem uma incerteza relativamente grande na determinação da posição do elétron.

Então a gente não sabe exatamente onde o elétron está, mas é capaz de dizer qual a probabilidade de encontrar o elétron em determinada região do espaço.
Como? Através das funções de onda!
A função de onda por si só não nos diz muita coisa. Ela não tem um significado físico. Ela é só uma função matemática. Mas quando a gente eleva ao quadrado.. tchatchatcharãmmm: surge a função densidade de probabilidade. Assim:
Como assim densidade de probabilidade?
Pensa que o orbital é uma nuvem. Uma nuvem mesmo, dessas do céu. A nuvem pode estar bem densa numa região e bem rarefeita em outra. E é assim também no orbital. Algumas regiões tem alta densidade de probabilidade de encontrar o elétron enquanto em outras essa probabilidade é baixa.
A densidade de probabilidade tem unidade , o que significa que, pra encontrar a probabilidade de encontrar o elétron num determinado volume a gente vai multiplicar a função densidade de probabilidade por um volume (). E encontrar uma probabilidade que vai ficar entre 0 (0% do elétron estar naquele volume) a 1 (100% de encontrar o elétron).
Vamos ver uma função de onda aí:
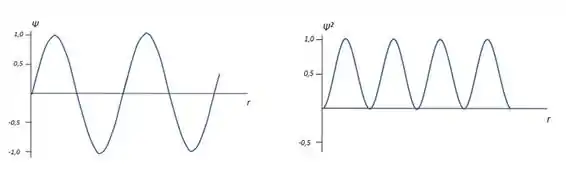
Quando a gente eleva ao quadrado, toda a função fica positiva.
Vamos dizer que é a distância em relação ao núcleo. Segundo essa função, quando a densidade de probabilidade de encontrar o elétron é zero. Essa probabilidade aumenta conforme aumenta e atinge um máximo. Então a densidade de probabilidade começa a cair, atinge o zero e volta a subir, porque não existe densidade negativa. E assim sucessivamente.
Cada ponto onde a densidade de probabilidade é zero é chamado nodo ou nós.
No nó:
A quantidade de nós presente em um orbital é igual a , onde é o nosso número quântico principal.
Os números quânticos
Como a gente viu, o número quântico surge naturalmente ao resolver a equação de energia do elétron.
Conforme as funções de onda foram sendo estudadas, outros números quânticos foram surgindo. Esses números são essenciais para descrever o orbital e o elétron.
Vamos dar uma olhada em cada um deles:
- Número quântico principal : É o mesmo que já estamos acostumados a ver em outros capítulos. O está intimamente ligado à energia do orbital, ao tamanho/volume do orbital e ao número de nós do orbital. pode assumir qualquer valor natural diferente de zero.
- Número quântico azimutal : Também é chamado de número quântico do momento angular ou número quântico secundário. O nos informa o formato do orbital e o número de superfícies nodais angulares. pode assumir qualquer número inteiro, mas o valor máximo permitido para é igual a . Como cada nível se divide em valores de , algumas vezes chamamos de subnível. Cada valor de tem uma letra correspondente.
- Número quântico magnético : O nos informa como o orbital está orientado no espaço. Se está sob o eixo x, entre o eixo x e o eixo y, etc. Ele pode assumir valores inteiros entre e . Logo, existem valores de em casa subnível.
- Número quântico de spin : Assim como o , o está ligado ao momento angular do elétron. Mas enquanto o se refere ao movimento do elétron ao redor do núcleo, o está ligado ao movimento do elétron em torno do seu próprio eixo (tipo a Terra que gira ao redor do Sol e em torno de si mesma).
![]()
Por exemplo, se ,
O elétron pode girar no sentido anti-horário (representado por ou ) ou no sentido horário (representado por ou ).
Representando um orbital
Enquanto descrevem o orbital em si, fala estritamente do elétron dentro do orbital.
Portanto, para descrever completamente o orbital, precisamos de .
Por exemplo, no orbital 1s o e o s corresponde a que só aceita .
No subnível 2p o e o p corresponde a . Para esse valor de , pode ser , que levam aos orbitais 2px, 2py e 2pz, cada um sobre o eixo x, eixo y e eixo z, respectivamente. Isso não quer dizer que o orbital 2px corresponde ao e etc. São designações diferentes.
Vimos que um orbital é representado por uma função de onda . Logo, para descrever uma função de onda também precisamos dos números quânticos. A gente vai representar assim:
Portanto:
Agora, tá ligado que a gente falou que o número quântico nos dava uma ideia do formato do orbital?
Vamos ver o formato dos orbitais para , ou seja, orbitais do tipo s, p, d, f.
Orbitais do tipo s
Os orbitais do tipo s são simétricos em relação ao núcleo.
A densidade de probabilidade num orbital 1s pode ser representada assim:

Quanto mais escura a imagem acima, mais “densa” a probabilidade é, maior a chance de encontrar o elétron.
Normalmente, para simplificar, a gente não representa a densidade de probabilidade, mas a superfície limite da função de probabilidade. Como se a gente pegasse essa nuvem aí de cima e colocasse um saco ao redor dela. Nesse caso, a representação do orbital 1s seria assim:
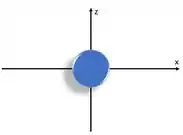
Para o 2s, fica a mesma coisa, porém maior.
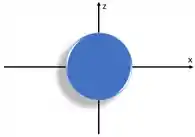
Mas a gente falou que o número de nós (probabilidade zero de encontrar o elétron) é igual a . Então, enquanto o orbital 1s tem 0 nós, o orbital 2s possui 1 nó. Na representação da superfície limite não conseguimos vê-lo, mas na representação da densidade de probabilidade ele aparece assim:

E aquela região clara entre duas partes escuras é o nó do orbital 2s. O mesmo vai acontecer pro 3s (2 nós), 4s (3 nós), etc.
Orbitais do tipo p
Os orbitais do tipo p tem o formato de duas esferas achatadas, assim:
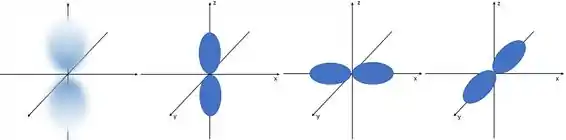
O primeiro desenho tá representando a função densidade, os outros são orbitais do tipo pz, px e py, nessa ordem. Então essa letrinha pequena indica sobre qual eixo o orbital p tá “deitado”.
Todos os orbitais do tipo p tem um nó no núcleo (origem dos eixos no nosso esqueminha).
Orbitais do tipo d
Como para existem 5 valores de (-2, -1, 0, +1, +2), existem 5 orbitais do tipo d. Vamos dar uma olhada nas superfícies limites desses orbitais.
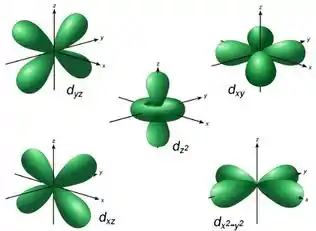
Orbitais do tipo f
Existem 7 orbitais do tipo f, que estão representados abaixo:
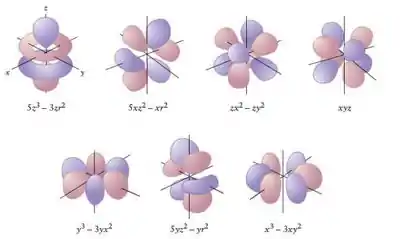
Nós
Não, não vamos falar sobre nós tipo eu e você. Vamos voltar a falar dos nós onde a probabilidade de encontrar o elétron é zero.
Ficava difícil falar disso antes de ver o formato dos orbitais.
Existem diferentes tipos de nós, dependendo do “formato” desse nó. Olha só:
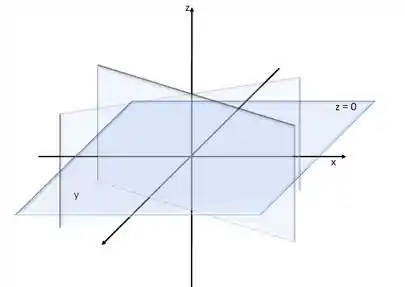
Vamos colocar o núcleo na origem do nosso eixo e escolher um ponto qualquer do espaço.
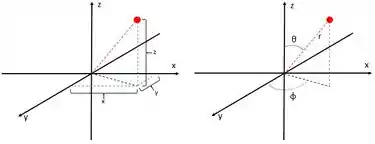
A gente pode definir esse ponto através do x, do y e do z que ele “ocupa”. Mas também pode definir através da distância em relação à origem (), o ângulo que o tracejado vermelho faz com o eixo z (letra grega theta θ) e o ângulo que o tracejado preto (sombra do vermelho no “chão” xy) faz com o eixo y (representado pela letra grega phi φ).
Lembra que o nó que aparece no orbital 2s era tipo uma esfera? Nesse tipo de nó a gente mantém o fixo e varia os dois ângulos formando a superfície de uma esfera. Como o raio é fixo, a gente chama esse tipo de nó de radial.
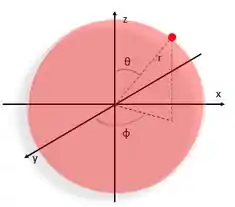
Agora, se a gente fixar um ângulo e variar o e o outro ângulo, a superfície formada não vai ser uma esfera. Ela pode ser um plano ou algo tipo um cone.
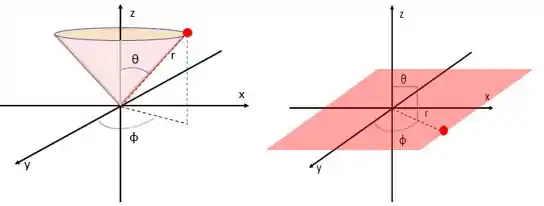
Pra esse tipo de nó onde um ângulo é fixo, a gente dá o nome de superfície nodal angular.
Calma lá, amigão. Aí vem os exemplos:
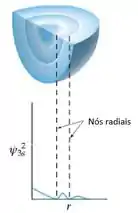
Toda vez que a função densidade de probabilidade do orbital 3s iguala a zero, a gente tem um nó radial assim:
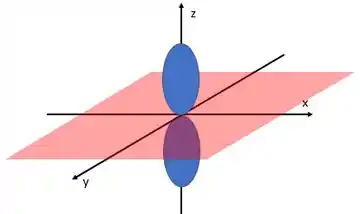
Nos orbitais p temos sempre uma superfície nodal angular planar assim:
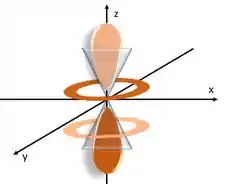
E aquela superfície nodal angular em formato de cone aparece, por exemplo, no orbital 3.
Antes de acabar (e eu juro que já tá acabando) vamos falar um pouquinho de quantidade.
Já falamos que o número de nós de um orbital é igual a .
Agora que temos dois tipos de nós você pode saber ainda que o número de superfícies nodais angulares é igual a . Então o número de nós radiais vai ser a diferença entre o número total de nós e os nós angulares, .
Beleza? Vamos fazer uns exercícios?
Schrödinger e os espectros de linhas
Função de onda, probabilidade e densidade de probabilidade
Os números quânticos
Representando um orbital
Orbitais do tipo s
Orbitais do tipo p
Orbitais do tipo d
Orbitais do tipo f
Nós
Exercícios Resolvidos
Exercício Resolvido #1
USP/IQSC – Lista de Exercícios de Química Geral. Estrutura Atômica. Questão 17.
Calcular a energia em joules, o comprimento de onda em metros e o número de onda em metros-1 de uma linha espectral produzida no espectro de hidrogênio quando um elétron decai da 4ª órbita de Bohr para a 1ª. Indique ainda a qual região do espectro eletromagnético pertence esta linha.
Passo 1
Por Bohr, a energia de cada camada é dada por:
Então, para calcular a diferença de energia entre duas camadas, vamos fazer assim:
Pelo enunciado, a gente vê que o elétron está pulando do para o . E a gente sabe que o valor da constante A é igual a:
Então vamos calcular a diferença de energia.
Passo 2
Para calcular a diferença de energia entre os níveis, então:
Como o elétron saltou de uma camada maix externa para uma mais interna a gente vai dizer que ele emitiu 2,04.10-18 J. Poque pra pular pra uma camada mais externa ele absorve energia e pra uma mais interna ele emite.
Beleza. E o comprimento de onda?
Passo 3
A gente viu que o elétron absorve e emite radiação através de fótons cuja energia é dada por:
E nessa fórmula aí de cima a gente sabe que é a constante de Planck (6,626.10-34 J.s) e acabamos de calcular que a energia é 2,04.10-18 J.
Bora calcular a frequência então:
Aquela unidade ali não é só porque a gente quer que seja não. Você pode e deve conferir as unidades de todo mundo aí de cima. Mas como todas as grandezas estão no SI, nossa resposta também tá no SI. É sempre bom trocar todas as unidades pro SI antes de jogar na fórmula!
Ainda temos que transformar aquela frequência em comprimento de onda.
Faz alguns capítulos que não fazemos isso né? Mas ainda é assim que se faz:
E 9,74.10-8 é o comprimento de onda em metros (como pedido) produzido no espectro devido ao pulo eletrônico.
Passo 4
Lembra como calcular número de onda? A unidade é uma dica e tanto!
Ela é o inverso do comprimento de onda e significa “quantas ondas a gente encontra em uma unidade de comprimento”, no caso o metro, porque o enunciado pediu assim. Vamos ver:
E o número de onda calculado é igual a 1,03.107 por metro!
Passo 5
A gente já cansou, mas o enunciado ainda pergunta em qual região do espectro esse comprimento cai.
Você pode:
- lembrar que quando a série do hidrogênio era de Lyman e a região é do UV.
- decorar que o visível vai de 400 nm (violeta) até 750 nm (vermelho) e ver que como esse comprimento de onda é menor que 400 nm ele cai no UV.
- olhar no espectro aí de baixo e ver que 9,74.10-8 m está no UV.

Resposta
.
.
.
Região do ultravioleta.
Exercício Resolvido #2
UFRRJ – 1ª Lista de Exercícios de Química Geral. Estrutura Atômica. Questão 1.20.
Um elétron no átomo de hidrogênio faz uma transição de um nível de energia de número quântico igual a para o estado com . Se o fóton emitido tem comprimento de onda de 434 nm, qual o valor de ?
Passo 1
A gente sabe que a energia de cada camada é dada por:
Onde é uma constante de valor J, que equivale a .
A diferença de energia entre duas camadas é, então:
Onde a gente usa pra resposta dar positiva (a gente fazia assim nas série de linhas).
Como o enunciado fala que um fóton foi emitido, a gente entende que ele pulou para uma camada mais interna e o é maior que o . Então o vai ser o nosso .
E a gente também já viu que o elétron pula de uma camada para outra absorvendo ou emitindo fótons. Sendo que a energia dos fótons é dada por:
A gente pode primeiro calcular a energia do fóton e depois jogar essa energia na equação que relaciona a energia das camadas, ou fazer tudo junto.. assim:
Lembrando que e que a frequência é igual a:
Sendo que m/s é a velocidade da luz e o comprimento de onda foi dado como .
A gente pode colocar tudo isso na mesma equação:
Passo 2
Se você preferir, pode ir calculando uma coisa de cada vez, ok?
Aqui vamos pegar aquela última equação que engloba tudo e resolver de uma só vez:
E o do enunciado, nosso , é igual a 5.
Resposta
.
Exercício Resolvido #3
UFRRJ – 1ª Lista de Exercícios de Química Geral. Estrutura Atômica. Questão 1.10.
Quais são os números quânticos? Que informação nos fornecem os números quânticos e ?
Passo 1
Os números quânticos são:
- Número quântico principal ;
- Número quântico azimutal ;
- Número quântico magnético ;
- Número quântico de spin
Passo 2
O número quântico principal nos dá uma ideia do tamanho do orbital. Ele se relaciona com a energia do elétron. Elétrons de mesmo se encontram na mesma camada da eletrosfera, isso porque o indica o quão afastado do núcleo o elétron pode estar.
O número quântico azimutal, também conhecido como número quântico do momento angular nos dá uma ideia do formato do orbital e de quantas superfícies nodais esse orbital apresenta. A cada valor de corresponde uma subcamada de uma camada . Como está relacionado ao momento angular do elétron, ele está relacionado com a energia cinética do mesmo.
O número quântico magnético distingue orbitais de uma mesma subcamada (), indicando sua orientação no espaço.
O número quântico de spin não fala do orbital em si, mas da orientação do elétron dentro do orbital, podendo assumir apenas os valor ou .
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 51-1.54.
Quais são os números quânticos principal e de momento angular do orbital, para cada um dos seguintes orbitais:
Passo 1
A representação dos orbitais é assim:
Ou seja, o número que vem na frente representa o , número quântico principal.
E a letra que vem depois, representa o , número quântico do momento angular.
Só precisamos lembrar que letra representa que valor de e depois é tranquilão. Olha aí:
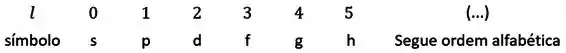
Passo 2
Então, beleza:
- 2s:
- 6f:
- 4d:
- 5p:
Resposta
- 2s:
- 6f:
- 4d:
- 5p:
Exercício Resolvido #5
UFRRJ – 1ª Lista de Exercícios de Química Geral. Estrutura Atômica. Questão 1.4.
Qual orbital tem maior energia: o orbital 2s ou 2p no átomo de hidrogênio? Isto também é válido para o He? Explique.
Passo 1
Em um átomo de hidrogênio, a energia é dada por:
Logo, ela só depende do número quântico principal .
Como, no enunciado, os dois orbitais possuem o mesmo (), para o hidrogênio ambos possuem a mesma energia. São orbitais degenerados.
Passo 2
O mesmo pensamento é válido para outros átomos com apenas 1 elétron (como o He+ ou o Li2+), que são chamados de átomos hidrogenóides.
Mas e pro He?
O He possui dois elétrons e o cálculo de energia dos seus orbitais é bastante diferente porque deve incluir, por exemplo, a repulsão entre os elétrons e a blindagem de um elétron sobre o outro (enfraquecimento da atração núcleo-elétron devido a presença de outros elétrons na eletrosfera).
Para átomos multieletrônicos, dentro de uma mesma camada (mesmo ) a energia é maior quanto maior for o número quântico azimutal ().
No caso, para a energia dentro de um mesmo nível:
E no átomo de He o orbital 2p é mais energético que o orbital 2s.
Resposta
Hidrogênio: ambos orbitais com mesma energia.
Hélio: 2p mais energético que 2s.
Exercício Resolvido #6
UFRRJ – 1ª Lista de Exercícios de Química Geral. Estrutura Atômica. Questão 1.41.
Quais dos seguintes conjuntos de números quânticos não são permitidos no átomo de hidrogênio? Para o conjunto que estiver incorreto, aponte a inconsistência.
Passo 1
Aqui a gente em que lembrar das restrições de cada número quântico. Vamos lá:
Pro número quântico principal não temos muitas restrições. Ele é um número inteiro positivo. Então pode assumir os valores:
Beleza?
O azimutal () é um número inteiro não negativo (o que inclui o zero) e varia de 0 até . Ou seja:
- Se ,
- Se ,
- Se
- Se ,
Os valores permitidos pro número quântico magnético () dependem do azimutal. é um número inteiro que varia de a . Assim:
- Se ,
- Se ,
- Se ,
- Se ,
E os valores do número quântico de spin () só podem ser .
Passo 2
Vamos analisar cada item do enunciado agora:
- OK
- ERRADO
- ERRADO
- ERRADO
- ERRADO
- OK
- OK
- ERRADO
- ERRADO
- ERRADO
Para o deve estar entre e .
não pode ser igual a 0.
não pode assumir valores negativos.
O máximo valor de é igual a . Aqui, o máximo valor permitido para é .
Os únicos valores permitidos para são e .
não pode assumir valores negativos.
só pode variar entre a .
Resposta
- Permitido
- Não permitido
- Não permitido
- Não permitido
- Não permitido
- Permitido
- Permitido
- Não permitido
- Não permitido
- Não permitido
Exercício Resolvido #7
UFRJ – Lista de Exercícios de Química Geral. Professor Jean Eon. Questão 6.
Descrever as características geométricas (superfícies nodais, distribuição eletrônica) do orbital atômico .
Passo 1
Os orbitais do tipo são caracterizados por duas esferas achatadas, com um plano nodal entre eles.
O orbital p pode ser do tipo , ou . Isso designa sobre qual eixo essas esferas achatadas estão.
No caso do , o orbital está disposto ao longo do eixo , mais ou menos assim:
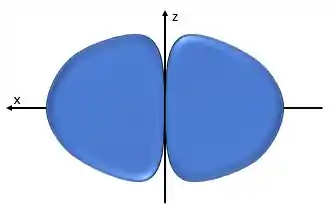
A gente precisa se ligar que esses desenhos de orbitais são só uma representação gráfica da superfície limite da função de probabilidade do elétron.
O que isso quer dizer?
O orbital é meio que uma nuvem. Existem pontos em que essa nuvem é muito densa (o que pra nós significa alta probabilidade de encontrar o elétron) e pontos onde ela quase não está presente (baixa probabilidade de encontrar o elétron).
Quando a gente desenha os orbitais como esse aí de cima, é como se a gente estivesse colocando uma “capa por cima da nuvem”... a gente vê o contorno da nuvem, mas não vê mais onde ela está densa e onde está “rarefeita”.
Por que isso é importante?
Por exemplo, aí em cima, a gente só enxerga um nó que seria ali no eixo . Mas a gente já comentou que o número de nós é igual a .
Como o orbital do enunciado é o , e o nosso orbital tem 2 nós!
Passo 2
Tá, mas como eu escrevo isso na prova?
Vamos tentar organizar melhor as ideias:
No orbital o número quântico principal é . Esse número está intimamente ligado a energia do orbital e ao volume do mesmo.
Além disso, ele nos informa que o orbital tem 2 nodos (onde a probabilidade de encontrar o elétron é nula), uma vez que o número de nodos é igual a . Desses dois nodos, temos uma superfície nodal angular (porque ) e um nodo radial (para completar os 2)
A superfície dos orbitais pode ser entendida como dois glóbulos achatadas um contra o outra, existindo um plano nodal entre elas.
Essas esferas estão dispostas sobre um eixo, designado, no caso do orbital pela letra . Nesse caso, a distribuição eletrônica é simétrica em relação ao plano .
Assim, uma representação do orbital pode ser vista abaixo.
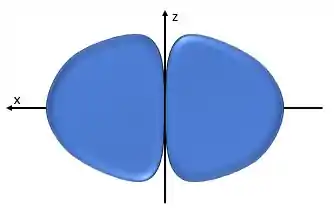
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #8
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 51-1.45.
- Faça um desenho da superfície-limite que corresponde aos orbitais 1s, 2p e 3d.
- O que se entende por um nodo?
- Quantos nodos radiais e superfícies nodais angulares tem cada orbital?
- Prediga quantos planos nodais são esperados para um orbital 4f.
Passo 1
- A gente tem uma ideia de como essas superfícies limites são. Como o enunciado não explicita sobre quais eixos devemos desenhar, vamos fazer sobre qualquer um. É legal desenhar o 3d maior que o 2p, e o 2p maior que o 1s porque, como a gente comentou, o número quântico principal dá uma ideia do tamanho dos orbitais. Valeu?
- Nodo é o ponto onda a função de onda (orbital) muda de fase.
- Primeiro vamos definir o que é um nodo radial e o que é uma superfície nodal angular.
- Para o orbital 4f:
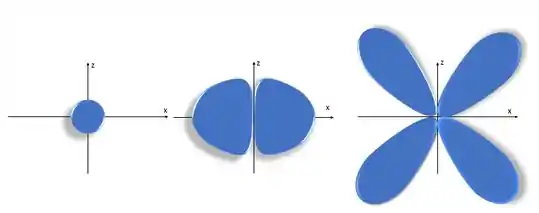
E aí estão os desenhos do 1s, 2p e 3d, respectivamente.
Passo 2
Isso basta!
Mas pra você entender um pouquinho melhor:
Lembra que o orbital nada mais é do que uma função matemática? Nem todas as funções matemáticas servem como função de onda. As funções de onda geralmente contém um “”, um “ ou outra função trigonométrica, que faça com que ela oscile, como uma onda.
Vamos olhar a função seno abaixo:
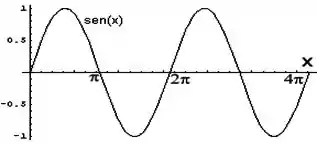
Cada vez que ela passa do positivo para o negativo ou do negativo para o positivo, dizemos que ela está mudando de fase.
A função seno acima muda de fase nos pontos e cada um desses pontos é chamado um nodo.
E lembra que a probabilidade de encontrar o elétron é igual ao quadrado dessa função?
Se a gente pegar a função aí de cima e elevar ao quadrado, todos os pontos negativos vão virar positivos (porque o quadrado de qualquer número é um número positivo).
Mas os pontos onde ela é zero, vão seguir sendo zero!
Pra um orbital, pra qualquer ponto onde a função de onda tiver valor zero, o quadrado dela também vai ser zero. E nesse ponto a probabilidade de encontrar o elétron é nula. Isso é o nodo!
Passo 3
A gente já viu que no nodo, a probabilidade de encontrar o elétron é nula. Mas a probabilidade igual a zero não fica em um único ponto. O orbital tem três dimensões! A probabilidade zero de encontrar o elétron se estende por uma superfície!
No orbital p, por exemplo, toda a superfície entre as duas esferas achatadas tem probabilidade zero de encontrar o elétron. Então para x=0 (todo o plano delimitado pelo eixos z e y) temos uma superfície nodal.
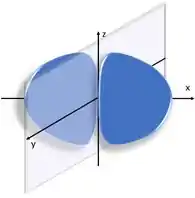
Agora, olhando para o orbital 2s, não existem planos nodais. No entanto, a gente calcula o número de nós (ou nodos) por . Como, para o 2s, , então temos um nó. Onde ele está? Lá dentro!
Em orbitais s, o nodo é definido por um determinado raio em relação ao núcleo. Ou seja, existe toda uma casca esférica delimitada por um certo raio de distância do núcleo onde a probabilidade de encontrar o elétron é nula.
Quando o nó é caracterizada por um raio fixo, chamamos de nodo radial.
Quando o nó não tem uma distância fixa do núcleo, existe um ângulo que é fixo (no nosso desenho é o ângulo do plano em relação ao eixo x, que é sempre de 90°) e temos uma superfície nodal angular (muitas vezes formando um plano).
Agora vamos falar de quantidade:
O número de superfícies nodais angulares é igual a . Ou seja: orbitais s não possuem superfícies nodais angulares, orbitais do tipo p possuem 1, e assim por diante.
Como o número de nós é igual a , o número de nós radiais vai ser dado pela diferença entre o número total de nós () e o número de nós angulares ().
Por exemplo:
3d: número de nós angulares: ; número total de nós: ; número de nós radiais: 0
5p: número de nós angulares: ; número total de nós: ; número de nós radiais: 3
4f: número de nós angulares: ; número total de nós: ; número de nós radiais: 0
Passo 4
Como vimos, com , o orbital 4f possue 3 superfícies nodais angulares. Não necessariamente elas serão planas.
Vamos dar uma olhada nos orbitais do tipo f:

Com excessão do orbital f, todos os outros apresentam 3 planos nodais, tipo assim:
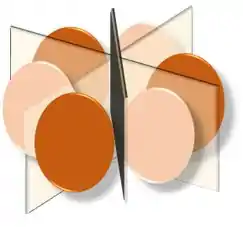
O orbital f apresenta 3 superfícies nodais angulares, mas apenas 1 é plana:
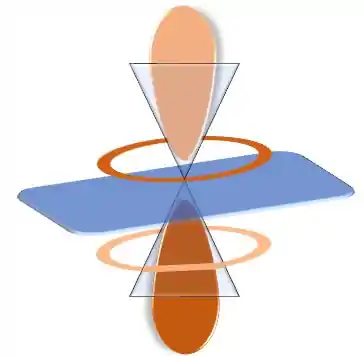
Onde os dois cones e o plano azul representam as três superfícies nodais angulares.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #9
UFMG - Lista de Exercícios de Química Geral. Estrutura Eletrônica. Questão 7.
- Complete a tabela abaixo:
- Utilizando diagramas de superfície limite, faça o desenho do orbital 2pz, indicando os eixos cartesianos envolvidos e os sinais das funções de onda.

Passo 1
- Vamos completar essa tabela aí!
- E pro desenho do orbital:
Quanto ao tipo de orbital: é só colocar a letra que representa cada valor de .
O número de orbitais em determinada subcamada é a quantidade de valores que o pode assumir, que no caso é .
E o número de superfícies nodais é igual a .

Passo 2
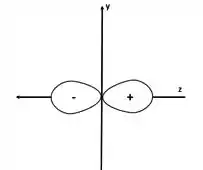
E aqui não faz a menor diferença se o eixo z tá em pé ou deitado e se o outro eixo é o y ou o x. Só tem que fazer os orbitais sobre o eixo z ok?
Além disso, essa coisa de + ou de – não tem nada a ver com carga. Tem a ver se a função é positiva ou negativa, mas isso não altera a probabilidade de encontrar o elétron em um ponto do espaço. Afinal de contas, pra probabilidade a gente usa o quadrado da função e todo mundo fica positivo!
Também não faz diferença em qual lado você coloca o mais e em qual você coloca o menos. Só precisa ter um de cada um.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #10
UFMG - Lista de Exercícios de Química Geral. Estrutura Eletrônica. Questão 9.
- Os três números quânticos de um elétron em um átomo de hidrogênio em um determinado estado são , , . Em que tipo de orbital esse elétron está localizado?
- Utilizando os eixos cartesianos próprios, faça um diagrama de superfície limite que ilustre o tipo de orbital descrito no item “a”. Indique o número de planos nodais e o número de nós radiais presentes.
Passo 1
- Com esse conjunto de números quânticos, estamos falando de um dos orbitais 3p. E o “tipo” de orbital é p.
- E pro diagrama de superfície limite do orbital, vamos desenhar o px, o py e o pz, respectivamente.
Passo 2
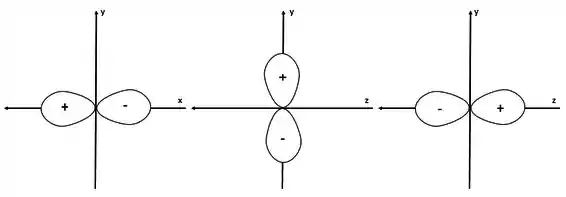
E aqui não faz a menor diferença qual eixo está em pé e qual está deitado. Só tem que fazer os orbitais sobre o eixo x, y e z respectivamente, ok?
Além disso, essa coisa de + ou de – não tem nada a ver com carga. Tem a ver se a função é positiva ou negativa, mas isso não altera a probabilidade de encontrar o elétron em um ponto do espaço. Afinal de contas, pra probabilidade a gente usa o quadrado da função e todo mundo fica positivo!
Também não faz diferença em qual lado você coloca o mais e em qual você coloca o menos. Só precisa ter um de cada um.
Orbitais p possuem 1 plano nodal. Já o nó radial depende do número quântico principal.
Como e o número de nós é igual a , temos 2 nós no orbital do item “a”. Sabendo que só um é plano, o outro é radial.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #11
UFRJ – Lista de Exercícios de Química Geral. Professor Jean Eon. Questão 7.
Considere os orbitais atômicos e , admitindo respectivamente as funções angulares e . Determine, na ordem seguinte, o número total de superfícies nodais, a natureza das superfícies nodais derivando da parte angular e o número de esferas nodais destes dois orbitais.
Passo 1
A nomenclatura mundou um pouco, mas vamos entender que superfícies nodais são as nossas superfícies nodais angulares e esferas nodais são os nossos nodos radiais.
A gente sabe que o número total de nodos é dado por .
Então as duas funções de ondas acima, e , com , possuem 3 nodos.
E a gente também sabe que o número de superfícies nodais angulares é igual a .
Logo, as duas funções de ondas acima, e , com , possuem 3 superfícies nodais angulares, não tendo nenhuma esfera nodal.
Passo 2
Como é que a gente descobre a “natureza das superfícies nodais”?
Através da função angular do orbital a gente pode definir se as superífices são planas e quais equações descrevem essas superfícies.
Vamos ver como isso funciona.
Para a primeira função de onda, a função angular é:
O nodo é quando a função de onda é zero né? Então vamos igualar esse cara aí a zero:
E pra uma multiplicação ser igual a zero, um dos fatores é zero:
E o que que é esse ? Ele é a distância de um ponto qualquer em relação à origem. Olha aí:
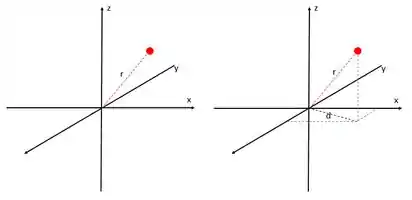
Aquela reta pontilhada em preto, que a gente chamou de d, é tipo a sombra da linha tracejada vermelha no “chão” (plano xy).
Por pitágoras, a gente vê que:
E então:
Aí a gente volta pra nossa função e substitui por , beleza?
O que que isso quer dizer?
Que a nossa função é igual a zero toda vez que:
é um plano, enquanto a outra superfície é bem mais complexa de enxergar. Normalmente teria que parametrizar e etc. Tem que ter uma base legal de cálculo. Mas são dois cones virados um contra o outro, assim:
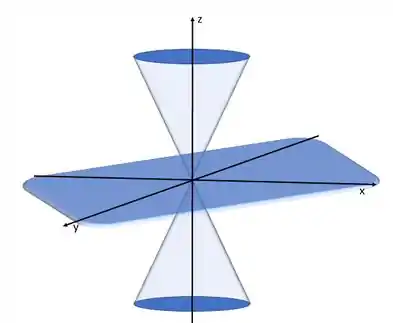
Vamos fazer a mesma coisa com a outra função:
Igualamos ela a zero e achamos:
Desenvolvendo a segunda equação:
Então a função é igual a zero sempre que ou .
Resposta
Ei, a resposta está no passo a passo :)