Fissão e fusão nuclear
Teoria
Oláaaa!
A gente já viu que a nível nuclear uma pequena variação de massa gera uma energia enooorme, né? No tópico anterior, a gente viu a energia liberada quando núcleons se juntam para formar o núcleo, a chamada energia de ligação nuclear.
Quando a gente divide essa energia de ligação nuclear pela número de núcleons envolvidos, a gente consegue um gráfico mais ou menos assim ó:
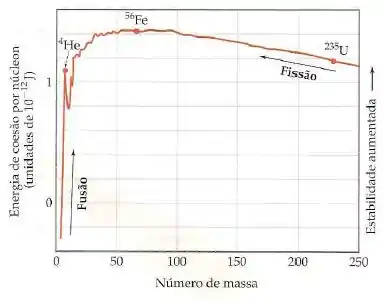
Nesse gráfico, a gente consegue ver que o ferro-56 e os metais próximos dele são mais estáveis, já que eles tem a maior energia de ligação nuclear por núcleon.
A forma do gráfico e a tendência dos átomos tem 2 consequências: os núcleos mais pesados vão se dividir em núcleos menores, para se estabilizarem, num processo chamado fissão.
Já os núcleos mais leves (com menor número de massa), vão se fundir com outros núcleos, num processo chamado fusão!
Como nesses processos (átomos leves sofrendo fusão e átomos pesados sofrendo fissão) o átomo vai se tornar mais estável, há liberação de energia!
Fissão nuclear induzida e espontânea
A fissão de um átomo pode acontecer naturalmente, quando o núcleo de átomos muito pesados se quebra em dois núcleos de massas semelhantes. Um exemplo de fissão nuclear espontânea é o amerício-244 (.
Já a fissão nuclear induzida é quando a gente bombardeia núcleos pesados com nêutrons. O bombardeamento com nêutrons faz com que o núcleo se quebre em dois!
Os núcleos que sofrem fissão quando bombardeados com nêutrons se chamam fissionáveis.
Alguns núcleos só sofrem fissão quando os nêutrons são acelerados, mas tem uns que conseguem fissionar mesmo com nêutrons lentos. Esses se chamam núcleos físseis, e o exemplo principal é o urânio-235 (, que é o principal combustível das usinas nucleares:
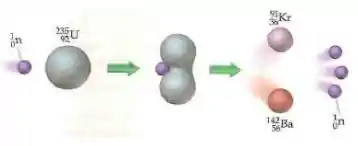
As fissões podem ocorrer de diversas maneiras, mas a maioria delas libera nêutrons no final. O interessante disso é que, com os núcleos físseis, as reações são autossustentáveis. Isso é: os nêutrons liberados na reação vão bombardear outros átomos de urânio, que vão gerar energia e mais nêutrons, e esses nêutrons vão bombardear outros átomos de urânio e....
Ou seja, os nêutrons são propagadores das reações de fissão induzidas!
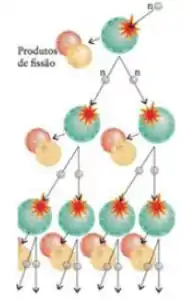
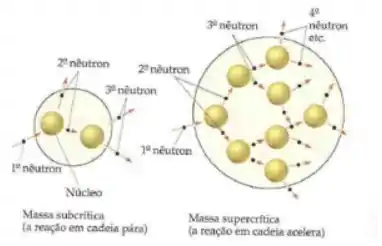
Para que isso aconteça, é necessário que os núcleos estejam próximos um dos outros, para que o nêutron liberado consiga atingir outro núcleo antes de escapar. O material físsil, então, deve ter uma certa massa mínima!
A massa mínima de material físsil para manter a reação em cadeia com velocidade constante de fissão é chamada massa crítica!
Se a amostra de núcleos for supercrítica, isso é, tiver uma massa acima da crítica, a reação corre risco de liberar energia demais e não ser controlada – causando uma explosão. Se a amostra for subcrítica, a reação em cadeia pode parar, porque os nêutrons podem escapar antes de atingir outro núcleo!
Bombas atômicas
As bombas atômicas usar muito o processo de fissão e o conceito de massa crítica.
Em Hiroshima, por exemplo, foi usada uma bomba de fissão onde duas massas subcríticas de urânio-235 eram arremessadas uma contra a outra, formando assim uma massa supercrítica. Já em Nagasaki, a técnica usada foi a implosão de uma massa subcrítica. Quando a gente implode uma massa subcrítica, o material físsil fica extremamente comprimido – e isso diminui sua massa crítica. Assim, a massa que a gente tinha antes se torna supercrítica – e explosiva!
No final, é usado um forte emissor de nêutrons (como o polônio), para dar o start da reação.
Produção de energia nuclear
A maioria dos reatores nucleares produzem energia através do processo de fissão de substâncias físseis (normalmente o urânio-235). Não é nosso interesse aqui explicar o passo-a-passo da produção de energia nuclear, mas sim te dar uma ideia do processo em geral!
Antes de mais nada, o combustível das usinas nucleares não são achados tão facilmente na natureza. É preciso enriquecer o urânio, para que a amostra tenha uma quantidade mínima de isótopo físsil (o urânio-235) – aproximadamente 3%.
Com esse urânio enriquecido, produz-se tubos de zircônio ou aço inox, os bastões de combustível. Usa-se também moderadores, substâncias que diminuem a velocidade dos nêutrons entre os bastões de combustível.
Além dos moderadores, existem bastões de controle, formados por núcleos que absorvem nêutrons (como o boro ou o cádmio), para diminuir a quantidade de nêutron disponível e diminuir a velocidade das reações. Assim, a usina consegue controlar a reação e evitar uma explosão.
Tudo isso, ainda que muito controlado, libera uma energia muito grande. Daí a necessidade de água – o líquido refrigerante – para resfriar todo esse processo e evitar que o reator superaqueça. Por isso as usinas se situam normalmente perto de rios
O problema desse rolê todo é que no final, produz-se 2 novos átomos + nêutrons, né? Esses 2 novos átomos são produtos extremamente radioativos, e cria-se um novo problema: o de estocagem dos dejetos radioativos, produtos da fissão.
Fusão nuclear
A fusão é o processo exotérmico onde 2 átomos pouco pesados se fundem, para criar um núcleo mais pesado. Com os elementos leves da tabela esse processo gera bastante energia, já que estabiliza os dois núcleos.
Para você ter noção da quantidade de energia liberada, as reações de fusão são responsáveis pela energia produzida pelo Sol! Alguns tipos de reação de fusão são:
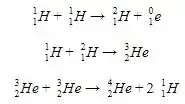
Lembrando que .
A gente pode ver nos exemplos a grande vantagem da fusão: não há produtos radioativos! Além disso, os isótopos mais leves (como o ) são bem mais disponíveis na natureza.
Maaas, a gente tem um probleminha: fazer dois núcleos cheio de cargas positivas se juntarem é complicado pela repulsão entre os núcleos! Por isso, a reações de fusão devem ser feitas em temperaturas altíssimas! (A gente também chama as reações de fusão de reações termonucleares, pela necessidade de altas temperaturas).
Olha só a reação de fusão entre o deutério e o trítio, dois isótopos do hidrogênio:
Os nêutrons adicionais diminuem a repulsão entre os núcleos, e por isso essa é uma das reações que menos precisa de temperatura. Ainda assim, a temperatura necessária é de 40.000.000 K!!!! Você viu porque faz sentido essas reações acontecerem no Sol, né?
Por essa questão da temperatura, ainda não se produz energia nuclear pelos processos de fusão ☹
Obs: as bombas de hidrogênio são bombas de fusão! Elas tem um poder de destruição 200x maior que as bombas atômicas como de Hiroshima e Nagasaki.
Obs2: as reações de fissão e fusão são como outras reações nucleares quaisquer, isso é, a gente pode calcular a energia envolvida nessas reações à partir da equação de Einstein!
Vamos dar uma praticada nesse mooonte de informação?
Fissão nuclear induzida e espontânea
Bombas atômicas
Produção de energia nuclear
Fusão nuclear
Exercícios Resolvidos
Exercício Resolvido #1
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, Exercício 17.69
Cada uma das seguintes equações apresenta uma reação de fissão. Complete e balanceie as equações:
a)
b)
c)
Passo 1
a) Para completar essas reações você tem só que lembrar daquele rolê da conservação do número de prótons e do número de massa 😊
Para descobrir qual é a partícula x, a gente tem que usar esses princípios!
A gente descobre, então, que a partícula x é um nêutron 😊
Passo 2
b) Mesmo esquema da a), mas agora essa fissão é induzida, e não mais espontânea...
Calculando o número de massa e de prótons pra preencher essa equação:
Assim, a gente vê que o núcleo que a fissão do urânio produz é o
Passo 3
c) Agora você já tá craque nisso, né:
Ou seja, essa reação produziu 3 nêutrons!
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Adaptada de Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, Exercícios 17.71 e 17.72
Diga se as seguintes declarações são verdadeiras ou falsas. Se falsas, explique por quê:
a) Quanto maior a energia de ligação por núcleon mais estável é o núcleo.
b) Núcleos físseis podem sofrer fissão quando atingidos por nêutrons lentos, mas nêutrons rápidos são necessários para a fissão de núcleos fissionáveis.
c) Uma massa subcrítica de material fissionável é instável e pode explodir.
d) Para que ocorra fusão, as partículas que colidem devem ter energia cinética elevada.
Passo 1
a) Verdadeira!
A questão só pede pra justificar as falsas mas vamos entender o porquê dessa ser verdadeira, né?
É pelo que tá escrito na letra a) que os fenômenos de fusão e fissão acontecem. Vamos pensar devagar: se a energia de ligação por núcleon é grande, isso quer dizer que eles estão fortemente ligados, né? Ou seja, para a gente quebrar essa ligação a gente vai ter que ceder muiiita energia e vai ser bem difícil: por isso eles são mais estáveis 😊 A fissão e a fusão acontecem porque os núcleos que não tem essa energia alta fazem de tudo pra ter (e, assim, se estabilizar!)
Passo 2
b) Falsa! É justamente ao contrário: núcleos fissionáveis são aqueles que se fissionam com qualquer estilo de nêutron, inclusive os lentos. Já os núcleos físseis precisam de nêutrons acelerados para serem fissionados.
Passo 3
c) Falso! Esse é o caso da massa supercrítica. A massa subcrítica não tem nêutrons suficientes para manter a reação em cadeia a uma velocidade constante, e a reação pode até mesmo parar. Já se a massa for supercrítica, a reação pode perder o controle e explodir!
Passo 4
d) Verdadeira!
As partículas na fusão precisam vencer a repulsão entre núcleos (cargas positivas) e, para isso, elas precisam de uma temperatura muito grande – o que acelera bastante as partículas e cede bastante energia pra elas! O difícil da fusão é justamente isso: como as partículas precisam de uma energia muito grande, essas reações são bem pouco feitas pra produção de energia.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Lista de exercícios UFPB – Prof Ary da Silva Maia
Assinale a alternativa que preenche corretamente a lacuna do parágrafo abaixo.O Sol é a grande fonte de energia para toda a vida na Terra. Durante muito tempo, a origem da energia irradiada pelo Sol foi um mistério pra a humanidade. Hoje, as modernas teorias de evolução das estrelas nos dizem que a energia irradiada pelo Sol provém de processos de _______ que ocorrem no seu interior, envolvendo núcleos de elementos leves.a) espalhamentob) fusão nuclearc) fissão nucleard) fotossíntesee) combustão
Passo 1
Essa questão é só para você se lembrar porque a fusão nuclear é tão complicada como processo de produção de energia: ela precisa de temperaturas altíssimas para acontecer. Além disso, ela produz muita energia (muito mais que a fissão). Por isso a resposta da questão é fusão nuclear (letra B), mas o que você tem que lembrar é: fusão acontece no Sol, precisa de temperatura muito alta, produz absurdos de energia!
E voilà! 😊
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Adaptado de lista de exercícios UFSC.
A fissão nuclear do urânio (U-235) ocorre após bombardeamento do mesmo por nêutrons, segundo a reação em cadeia:
Dentre as afirmativas abaixo, estão corretas:
a) O valor de y que torna a equação verdadeira é 94.
b) A formação de dois nêutrons assegura a propagação da reação em cadeia;
c) Um dos produtos formados possui número atômico superior ao do urânio.
d) O valor de x que torna a equação verdadeira é 58.
Passo 1
Vamos lá! Antes de mais nada, vamos completar essa equação usando o que a gente já sabe, os princípios de conservação de número de prótons e de nêutrons 😊
Se você tiver uma tabela periódica, só procurar o número atômico do Bário, se não, só calcular:
Passo 2
Agora vamos olhar pras afirmativas!
a) Já vimos, completando a equação, que essa afirmativa está certa! O número de massa do potássio nesse caso é 94.
b) O que assegura a propagação da reação não é só a quantidade de nêutron formado, e sim quantas gramas de urânio estão formando esses nêutrons! Ou seja, a gente depende da massa (para podermos comparar ela com a massa crítica!). Essa é falsa.
c) Falsa! É impossível, em uma fissão (onde a ideia é dividir o núcleo), que algum dos átomos tenha mais prótons que o urânio. Nesse caso teríamos uma fusão!
d) Falso, vimos no passo aqui em cima que é 56 o valor de x.
Resposta
Letra A
Exercício Resolvido #5
Adaptado de KOTZ, J.C. e TREICHEL Jr., P. Química e reações químicas. 4ª ed. Trad. J.A.P. Bonapace e O.E. Barcia. Rio de Janeiro: Editora LTC, 2002, Exercício 51.
Se a quantidade de urânio fissionável no mundo se tornasse escassa, ainda seria possível produzir energia, mas com um outro núcleo físsil, como o P1lutônio. O plutônio é produzido em reatores que produzem mais energia que consomem, em um processo que segue as seguintes etapas:
a) o emite uma partícula e se transforma em , emitindo uma partícula .
b) emite uma partícula beta e decai para um isótopo do neptúnio.
c) Esse isótopo do neptúnio decai por emissão beta e dá origem a um isótopo do plutônio.
O isótopo do plutônio é fissionável. Quando ele colide com um nêutron uma fissão acontece e pelo menos 2 nêutrons e 2 outros núcleos são liberados como produtos. Escreva a equação de cada uma das etapas e descubra quem é o isótopo do plutônio fissionável.
Passo 1
Essa questão toda é bem batida, ein! Parecido com o que a gente tem feito. A gente só precisa montar as equações com os dados e usar os princípios de conservação de massa e de número de prótons.
Vamos lá!
a)
Calculando a e z...
Ou seja, a partícula emitida é um nêutron!
Passo 2
b)
O número de prótons do neptúnio é só a gente olhar na tabela, né? Mas se você tá sem uma tabela aí, a gente também pode calcular
E o número de massa:
O isótopo é o neptúnio-239.
Passo 3
c)
Igual à letra b, a gente pode ver o número de prótons na tabela, e só precisa calcular a massa, que também vai ser 239! Ou seja, o isótopo é o plutônio-239.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #6
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, Exemplo 17.6
Quando os núcleos de urânio-235 são bombardeados com nêutrons, eles podem quebrar-se de várias maneiras como esferas de vidro que se partem em fragmentos de tamanhos diferentes. Em um dos processos, o urânio-235 forma bário-142 e criptônio-92:
Calcule a energia liberada (em joules) quando 1g de urânio-235 sofre essa reação de fissão. As massas das partículas são:
Passo 1
Para calcular a energia envolvida nessa reação, vamos ter que usar a equação de Einstein!
Onde . A energia da reação vai depender da variação de massa que ocorre na reação, que pode ser calculada por:
Então vamos lá!
A massa dos produtos é:
A massa dos reagentes:
Assim, a variação de massa da reação vai ser:
Para usar a equação de Einstein, a gente precisa que todos os valores estejam no SI!
Passo 2
A gente calculou a energia de quando 1 átomo de urânio reage! Agora, precisamos calcular para 1g 😊
Como a massa molar do urânio é para 1g...
A energia é imeeeensa, o que é de se esperar, já que o urânio é um combustível comum em usinas nucleares!
Resposta
Exercício Resolvido #7
Elaboração Própria.
O processo de fissão nuclear é bastante utilizado na produção de energia elétrica em alguns países por produzir uma excelente quantidade de energia térmica. Porém, um grande malefício promovido pela fissão nuclear é a produção de lixo radioativo, que deve ser armazenado em local apropriado. Esse lixo geralmente é composto por elementos químicos formados durante o processo de fissão. Assim, qual dos processos abaixo representa um processo de produção de lixo radioativo, ou seja, uma fissão nuclear?
a) .b)
c) .
d) .
Passo 1
Vamos lá! Primeiro, vamos analisar o que ocorre em cada alternativa:
Nessa reação, podemos observar que o átomo de Nitrogênio é bombardeado por um próton, formando o Carbono e a emissão de um Hélio. Isso se caracteriaza como uma Transmutação Nuclear.
Nessa reação, podemos observar que o temos dois isótopos de Hidrogênio no reagente (Deutério e Trítio). Eles são combinados, emitindo uma partícula nêutron e formam um átomo de Hélio. Isso se caracteriza como uma Fusão Nuclear.
Nessa reação, podemos observar que o Carbono emite uma partícula e forma um átomo de Nitrogênio. Isso se caracteriza como uma simples Reação Nuclear.
Nessa reação, podemos observar que o átomo de Urânio é bombardeado por uma partícula nêutron, emitindo em seguida 2 partículas nêutrons e gerando dois átomos diferentes: . Isso se caracteriza como uma Fissão Nuclear.
Resposta
d)
Exercício Resolvido #8
Elaboração Própria.
Alguns exemplos de materiais que podem ser utilizados nos reatores de fissão nuclear, por serem físseis, são:
De acordo com o exposto, podemos afirmar que um material físsil é aquele que é capaz de originar
a) dois ou mais núcleos atômicos menores.
b) um único núcleo atômico menor.
c) dois ou mais núcleos atômicos maiores.
d) um único núcleo atômico maior.
Passo 1
Vamos lá! Primeiro, vamos relembrar os tipos de fissão nuclear que existem:
A fissão de um átomo pode acontecer naturalmente, quando o núcleo de átomos muito pesados se quebra em dois núcleos de massas semelhantes. Um exemplo de fissão nuclear espontânea é o amerício-244.
Já a fissão nuclear induzida é quando a gente bombardeia núcleos pesados com nêutrons. O bombardeamento com nêutrons faz com que o núcleo se quebre em dois. Alguns núcleos só sofrem fissão quando os nêutrons são acelerados, mas tem uns que conseguem fissionar mesmo com nêutrons lentos. Esses se chamam núcleos físseis, e o exemplo principal é o urânio-235
Sabendo disso, podemos concluir que um material físsil é capaz de originar dois ou mais núcleos atômicos menores.
Resposta
a) dois ou mais núcleos atômicos menores.