Encontre e .
Passo 1
Opa! Vamos ver mais essa derivada aqui😊
Queremos encontrar e dado .
Como a gente tem duas um quociente de funções sendo divididas, vamos usar a regra do Quociente, que é assim:
Onde aqui a gente pode chamar:
Passo 2
Vamos precisamos fazer as derivadas de e agora:
Para , vamos lembrarlembrando da regra do tombo:
E pra , vamos lembrar que a derivada de uma constante é zero, e a derivada da exponencial é ela mesma:
Beleza! Já temos tudo que precisávamos. Vamos montar a Regra do Quociente agora!
Passo 3
Substituindo...
Multiplicando ali em cima:
Pronto! Essa é a primeira derivada!
Passo 4
Vamos pra segunda derivada agora! A gente vai usar a regra do quociente de novo, vamos derivar essa aqui:
Vamos calcular cada derivada dessas então...
Passo 5
Essa aqui primeiro:
Aqui a gente tem uma constante, uma exponencial e um produto. Vamos derivar cada pedacinho:
Vamos ver esse pedacinho aqui: . Aqui temos um produto, então a gente aplica a regra do produto:
Juntando tudo, nossa derivada de é:
Beleza! Essa já foi... vamos pra !
Passo 6
Agora vamos pra essa aqui:
Vamos reescrever assim:
Aqui vamos aplicar a Regra do Produto:
Prontinho! Mais uma derivada pronta! Vamos jogar isso tudo na regra do Quociente agora...
Passo 7
Pra relembrar: a gente achou:
Vamos substituir isso aqui agora:
Ficou feio né? Vamos dar uma resolvida nessas multiplicações ali pra ver se fica melhor. Repara que temos dois grandes termos no denominador, e que o está nos dois::
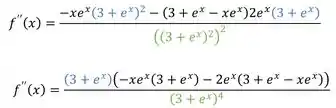
Também resolvemos a parte do denominador que possuía uma potência de uma potência, então repetimos a base e multiplicamos o expoente.
Repara agora que temos , multiplicando e dividindo, então podemos cortar um de cima com um de baixo, ficando com:
Agora vamos resolver as multiplicações do numerador:
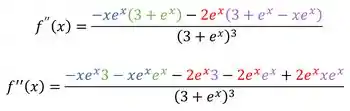
Organizado:
Agora, podemos juntar os temos que forem semelhantes:
![]()
E... finalmente chegamos em !
Prontinho! Calculamos 😊