Modelos fluídicos
Teoria
Introdução
E aí pessoal, tudo certinho?
Continuando nossa jornada pelo caminho da modelagem de processos, vamos agora dar uma olhadinha nos processos onde nosso principal objetivo será fazer o controle de um fluido em um sistema. Como por exemplo o tanque de nível abaixo:
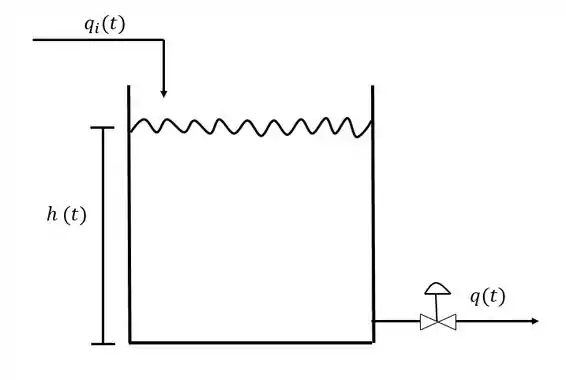
Nesse sistema, temos uma corrente de entrada e uma corrente de saída e precisamos controlar o nível do fluido no tanque, o nosso . Para isso, utilizamos a válvula na corrente de saída para controlar a quantidade de fluido que sai do nosso tanque. A dinâmica da válvula geralmente é um dado do problema, para o nosso exemplo vamos assumir a seguinte expressão para a vazão que passa pela válvula:
Onde é a resistência da válvula à passagem de fluido. Para esse sistema consideraremos uma densidade constante do fluido e que o tanque tem uma área de base .
Agora precisamos ver como as correntes de entrada e de saída estão relacionadas com a altura do tanque. Bora lá?
Balanço de Massa
Para determinar essa relação, a primeira coisa que devemos fazer é o nosso balanço de massa. Você não lembra como faz balanço de massa? Pega na minha mão e vem comigo.
A expressão geral do balanço de massa é a seguinte:
Opa, a gente tem alguma reação no nosso sistema? Não, né? Isso é ótimo, porque assim poderemos cortar os dois últimos termos do balanço de massa, que vai ficar com a seguinte cara então:
Vamos analisar cada um desses termos agora. Acúmulo quer dizer o tanto que a massa do sistema varia com relação ao tempo, em termos de derivada ficaria assim:
Para deixar tudo em termos de volume:
Então:
Já a quantidade que entra, é determinada pelo , que é a vazão de entrada:
Novamente fazendo a substituição:
Da mesma forma, a corrente de saída é:
O nosso balanço de massa então ficou da seguinte forma:
Para o nosso sistema, nós consideraremos constante, e sendo assim podemos cancelar ele em todos os termos.
Mas pera aí. Eu disse lá no começo que o nosso objetivo é controlar a altura do tanque , lembra? E ela não está aparecendo em nenhum lugar da nossa equação do balanço de massa. Então precisamos achar alguma forma de inserir a altura na nossa expressão.
O volume de fluido no tanque é a base vezes a altura de fluido, e como a área da base é constante:
Além disso, a vazão de fluido que passa pela válvula também é determinada pela altura do tanque, então:
Finalmente, chegamos à expressão final do nosso balanço de massa:
Linearização
Lindo! Incrível! Maravilhoso! Fizemos nosso balanço de massa com maestria, conseguimos chegar numa EDO que relaciona a altura do tanque, , com a vazão de entrada do tanque, . Mas agora temos um novo problema. A EDO que nós encontramos não é linear. Isso acontece devido ao termo . Portanto, precisamos fazer nossa linearização. Partiu?
Para fazer essa linearização a gente sempre vai usar a linearização de Taylor conforme essa expressão aqui:
E a nossa expressão que precisa ser linearizada é:
Na maioria dos nossos problemas em controle de processos, será interessante para nós fazer a nossa linearização em torno do ponto inicial, isso vai facilitar os nossos cálculos e permitir um controle mais eficaz. Sendo assim, aqui nesse caso o será que é a altura do nível do tanque no instante inicial.
Então, para determinar o primeiro termo da linearização é só substituir o por :
Agora, devemos derivar nossa expressão no ponto escolhido, ou seja, :
E por fim, porém não menos importante:
Agora é só juntar tudo e ser feliz:
Variáveis desvio
Agora a gente já está quase lá. Você já pode ver a luzinha no fim do túnel do sucesso, mas ainda tem mais um passo para que o seu modelo do nível do tanque fique tão perfeito quanto você, que é a introdução das variáveis desvio. Mas antes, vamos dar uma olhadinha como está nossa expressão depois da linearização:
Tá grande, né? Meio esquisita. Vamos então reescrever a mesma expressão, mas agora com todas as variáveis em seu ponto inicial:
Repare que o último termo sumiu porque .
Então agora, para que a gente consiga introduzir as nossas variáveis desvio, precisamos fazer a diferença entre essas duas equações. Vai ficar assim ó:
Agora é a hora do truquezinho maroto. Vamos substituir essas diferenças que estão atrapalhando a gente por novas variáveis, as variáveis desvio:
E agora pode comemorar, soltar fogos, pular, abraçar a mãe que chegamos ao fim da nossa modelagem:
O passo a passo para introduzir variáveis desvio fica assim então:
- Escrever a sua equação normal;
- Reescrever a equação substituindo todas as funções que dependem do tempo pelo seu valor no tempo inicial;
- Subtrair a segunda equação da primeira;
- Definir as variáveis desvio;
- Fazer a substituição.
Partiu ver outros casos nos exercícios?
Balanço de Massa
Linearização
Variáveis desvio
Exercícios Resolvidos
Exercício Resolvido #1
Professor Lizandro Sousa, UFF, lista 1, 2019.2, Exercício 5
Dois tanques são conectados conforme ilustrado na figura abaixo:
Desenvolva o modelo matemático para esse sistema de maneira a encontrar a variação do nível dos tanques e .
Passo 1
Vamos começar pelo primeiro tanque. O primeiro passo é sempre começar pelo balanço de massa:
Podemos desconsiderar os dois últimos termos porque não tem reação no tanque e portanto, nada é gerado nem consumido.
O termo de acúmulo a gente sempre representa como a derivada, a corrente entra no tanque e as correntes e saem do tanque:
Substituindo tudo no balanço:
Entretanto o exercício pede que a gente encontre a expressão de variação de , e não de . Sendo assim, precisamos fazer algumas substituições. Sabendo que:
E
Logo:
Substituindo na EDO:
Considerando a área e a densidade constante, teremos:
Passo 2
Vamos fazer o mesmo para o segundo tanque agora.
O segundo tanque também não tem nenhum consumo nem geração, mas também não tem nenhuma corrente entrando, sendo assim:
Como a única corrente que entra no segundo tanque é a corrente , o balanço ficará assim:
Agora vamos fazer o mesmo procedimento que fizemos para o primeiro tanque para encontrar a expressão de :
Portanto:
Considerando e constantes, teremos:
Resposta
Exercício Resolvido #2
Professor Lizandro Sousa, UFF, lista 1, 2019.2, Exercício 1
Um tanque de mistura mostrado na figura seguinte com volume de líquido e densisdade constante é usado para misturar duas correntes.
- Assuma que o processo está operando por um longo período de tempo com uma vazão mássica de entrada de e e composição das correntes de entrada de e . Nesse contexto, qual é o estado estacionário de ?
- Desenvolva o modelo matemático do sistema supondo que o nível de líquido possa variar.
Passo 1
Para determinar a composição de saída, precisamos fazer o balanço de massa para o componente.
Não existe reação no processo, portanto os termos de reação e consumo serão nulos. Além disso, também não existe acúmulo porque o enunciado diz que o volume não vatia e as composições são constantes.
Portanto:
Sabendo que as correntes e são as correntes de entrada e a corrente é a corrente de saída, teremos:
Substituindo os valores do enunciado:
Passo 2
Primeiramente vamos fazer o modelo para o volume de líquido no tanque. Vamos fazer o balanço de massa geral:
Novamente não temos reação, portanto sem acúmulo e sem geração:
Fazendo:
Como é constante, podemos passar ele dividinfo para o outro lado:
Passo 3
Vamos fazer agora o modelo matemático para a composição de saída . Para isso, devemos considerar que o modelo está em parâmetros concentrados, ou seja, o tanque é perfeitamente misturado e a composição no interior do tanque é igual à composição da saída. Vamos partir da expressão de balanço de massa geral que encontramos no passo anterior:
Agora vamos escrever o balanço de massa por componente:
Vamos aplicar a regra do produto no termo do acúmulo:
Substituindo no balanço:
Rearranjando:
Como:
Podemos substituir no balanço:
Vamos cortar que da pra cortar:
Por fim:
Se você quiser escrever as respostas em termos de volume, é só substituir por :
Resposta
a)
b)
Exercício Resolvido #3
Professor Eduardo Stockler Tognetti, UNB, lista 1, 2012.2, Exercício 6
Considere um tanque com fluxo de reciclo (recirculação)mostrado na figura abaixo. Objetiva-se estudar a dinâmica do nível , de acordo com o fluxo de entrada, , e a abertura das válvulas, . Considere densidade, , a área do tanque, , e a vazão de saída, , como constantes. Obtenha o modelo matemático do processo.
Passo 1
Vamos começar fazendo o balanço de massa para esse tanque então:
Não existe reação no processo, portanto os termos de reação e consumo serão nulos.
Passo 2
Vamos colocar tudo em termos de volume:
Substituindo tudo
Podmeos então cancelar em toda a equação.
Precisamos da expressão para a altura do nível no tanque, então:
Passo 3
Tamo quase lá, mas o exercício também pede para que a gente relacione o nível do fluido no tanque com a abertura da válvula, . Como:
Passo 4
Repare que caímos numa EDO não-homogênea, isso é, ela apresenta uma constante, . Quando acontece isso, precisamos aplicar variáveis desvio.
Atualmente, nossa EDO é a seguinte:
Vamos reescrever essa EDO colocando todas as variáveis com seus valores no estado inicial:
Como é uma constante, seu valor não se altera. Agora, nós subtraímos a segunda expressão da primeira:
Vamos definir as nossas variáveis desvio:
Substituindo na EDO:
Conseguimos então transformar uma EDO não-homogênea em uma EDO homogênea.
Resposta
Exercício Resolvido #4
Smith & Corripio, Princípios e Prática do Controle Automático de Processos, 3ª ed. Rio de Janeiro: LTC, 2012, pag 136, Exercício 4-9. Adaptado
Considere dois reatores de reservatório sob agitação em série com reciclo mostrado abaixo:
Você pode supor o seguinte:
- Cada reator está perfeitamente misturado e a temperatura é constante.
- Os volumes, e , são constantes e tabém as densidades das misturas que estão reagindo.
- O fluxo de entrada, , e o fluxo de reciclo, , são constantes.
- A reação química é basicamente de primeira ordem, e a taxa de ração é dada por .
- Os reatores estão inicialmente em estado estacionário com uma concentração de entrada .
- O retardo de transporte entre os reatores é desprezível.
Determine o modelo matemático para a concentração de no primeiro e no segundo reator.
Passo 1
Vamo fazer o balanço molar para o componente no primeiro reator:
O componente é um reagente do processo, logo ele é consumido e a expressão do balanço fica:
Vamos escrever termo a termo:
A corrente de saída é a soma das duas correntes de tanque que entram no primeiro reator, isso porque os volumes dos reatores são constantes.
Juntando tudo:
Passo 2
O balanço para o segundo reator:
Fazendo termo a termo:
Juntando tudo:
Resposta
Exercício Resolvido #5
Smith & Corripio, Princípios e Prática do Controle Automático de Processos, 3ª ed. Rio de Janeiro: LTC, 2012, pag 134, Exercício 4-4. Adaptado
A seguite reação elementar irreversível ocorre no reator elementar mostrado abaixo:
A velocidade de consumo do regemnte é dada por:
O conteúdo do reator está perfeitamente misturadao e a temperatura, o volume e a densiadade da mistura reagida podem ser consideradas constantes.
Suponha que as concentrações de entrada, , são constantes. Obtenha o modelo matemático para essas concentrações em função dos fluxos de entrada.
Passo 1
Dessa vez, em vez de fazer o balanço de massa, vamos fazer o balanço molar para o componente (que dá no mesmo no fim das contas)
O componente é um reagente do processo, logo ele é consumido e a expressão do balanço fica:
Vamos escrever cada parcela do balanço separadamente:
Juntando tudo:
Passo 2
Como o volume do tanque é constante, o que entra é igual ao que sai, sendo assim:
Subtitindo na expressão:
Passo 3
A gente já tá quase lá. O problema é que encontramos o EDO não linear, isso acontece porque existem termo com produtos de funções que dependem do tempo, e por isso precisamos linearizá-las.
A linearização ficará assim:
Os termos com barra representam o valor daquela variável em .
Caso você não se lembre como fazer a linearização, dá uma revisada nesse assunto porque é bem importante.
Substituindo na EDO:
Passo 4
Agora, ficamos com uma EDO não-homogênea por causa das constantes solta. Precisamos inserir então as variáveis desvio. A nossa EDO tá assim:
Vamos reescrever essa EDO com todas as variáveis com o valor inicial:
Definindo as variáveis desvio e fazendo a primeira menos a segunda, teremos:
Rearranjando:
Para o componente , a resolução é de forma análoga:
Resposta
Exercício Resolvido #6
Prof. Heraldo L. S. Almeida – Modelagem matemática de sistemas físicos – Escola politécnica UFRJ – Exercício 4.32
Determine o modelo matemático que descreve a posição do pistão em função da pressão na câmara, , e da força, , aplicada.
Passo 1
Para determinar a posição do pistão precisamos fazer o equilíbrio de forças sobre o pistão. Sendo assim:
Ou seja, a força resultante no pistão é igual ao somatório de forças.
Passo 2
A força resultante no pistão é igual a sua massa vezes a aceleração (segunda lei de Newton).
Para determinar o somatório de forças vamos considerar a força da esquerda para direita positiva e da direita para a esquerda negativa. Então:
O fluido no pistão faz força para a direita e a força aplicada, , é para a esquerda.
Juntando tudo:
Passo 3
Precisamos de uma expressão para a posição do pistão, . Para isso, devemos lembrar que a aceleração é a derivada da velocidade no tempo, e a velocidade, por sua vez, é a derivada da posição no tempo. Então:
Portanto:
Resposta
Exercício Resolvido #7
Seborg, Process Dynamics and Control, 4ª ed.: Wiley, 2016, pag 34, Exemplo seção 2.4.6 - Adaptado
A seguite reação elementar irreversível ocorre em um reator CSTR mostrado abaixo:
A velocidade de consumo do regente é dada por:
O conteúdo do reator está perfeitamente misturadao e a temperatura, o volume e a densiadade da mistura reagida podem ser consideradas constantes. A vazão de entrada, , também é constante.
Encontre a função de transferência . Onde e são as variáveis desvio de e .
Passo 1
Começando pelo balanço material para o componente :
O componente é um reagente do processo, logo ele é consumido e nada é gerado, a expressão do balanço fica:
Vamos escrever cada parcela do balanço separadamente:
Como o tanque está bem misturado, a concentração da saída é igual à do próprio tanque, e como volume é constante, a vazão de entrada é igual à de saída:
A taxa dado é em base volumétrica, logo, precisamos multiplica-la pelo volume do tanque:
Juntando tudo:
Passo 2
O nosso modelo matemático já está pronto, entretanto, o exercício pede a função de transferência o que significa que precisamos trabalhar um pouquinho mais em cima da nossa EDO.
Reorganizando a EDO:
Devemos então aplicar a transformada de Laplace na expressão, mas antes, devemos sempre alicar as variáveis desvio na EDO.
Vamos reescrever toda a equação com suas funções de tempo no estado estacionário () e vamos representar isso com uma barra sobre a variável:
Fazendo :
Definindo as variáveis desvio e substituindo em , teremos:
Nesse caso a nossa EDO não mudou muito, porque se trata de uma EDO homogênea. Entretanto, mesmo quando estamos trabalhando com EDO’s Homogêneas, é bom aplicar as variáveis desvio.
Passo 3
Agora que já aplicamos as variáveis desvio, já podemos usar transformada de Laplace na nossa EDO:
Transformadas de Laplace é um tópico muito importante e para achar fuções de transferência ele é primordial. Caso você não se lembre como alicar essa operação, seria uma boa ideia dar uma revisada nesse conteúdo.
Prosseguindo: vamos colocar em evidência:
Por fim, a função de transferência
Resposta
Exercício Resolvido #8
Elaboração própria
Encontre a função de transferência
Sabe-se que:
Considere constante.
Passo 1
Vamos começar pelo primeiro tanque. O primeiro passo é sempre começar pelo balanço de massa:
Podemos desconsiderar os dois últimos termos porque não tem reação no tanque e portanto, nada é gerado nem consumido.
O termo de acúmulo a gente sempre representa como a derivada, a corrente entra no tanque e as correntes e saem do tanque:
Substituindo tudo no balanço:
Mas:
E:
Substituindo no balanço, e simplificando :
Passo 2
Vamos reorganizar a equação e passar tudo que tem para o lado esquerdo:
Antes de aplicarmos a transformada de Laplace devemos fazer a inserção das variáveis desvio.
Reescrevendo a equação acima no estado estacionário ()
Fazendo a de cima menos a de baixo:
Definindo as variáveis desvio e substituinto na EDO:
Passo 3
Aplicando Laplace:
Isolando :
Por fim:
Passo 4
Agora devemos fazer o mesmo para o segundo tanque. O desenvolvimento é praticamente igual, sendo assim, vamos pular algumas etapas.
Do balanço de massa:
Substituindo e simplificando :
Rearranjando a equação:
Aplicando variáveis desvio:
Aplicando Laplace:
Passo 5
O exercício pede a função de transferência , entretanto, temos:
Ou seja, se multiplicarmos as duas funções de transferências, conseguiremos a resposta que desejamos:
Logo: