Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Modelos térmicos

Ver Todos os Exercícios

Teoria

Introdução

E aí, tudo na paz? Pronto para aprender mais um tipo de modelagem de processos?

Agora iremos ver um pouco sobre os processos térmicos. Aqueles que o nosso principal objetivo é entender o comportamento da energia em um sistema, ou em outras palavras, da temperatura.

Por exemplo, olha só esse amorzinho aqui:

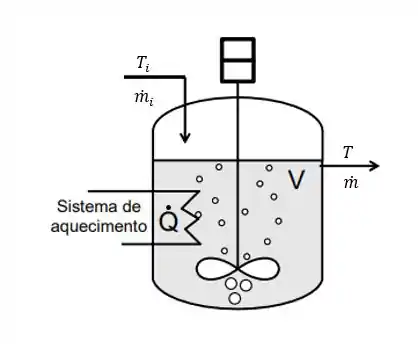
Aqui, nós temos um tanque. Nesse tanque existe uma corrente de entrada m ˙ i (mássica) com uma temperatuta T i , e também uma corrente de saída m ˙ (mássica) com uma temperatura T . Além disso também temos uma fonte de aquecimento via serpentina Q ˙ e um sistema de agitação.

Nosso objetivo aqui, vai ser saber como a temperatura no tanque vai variar dado todo esse cenário que a gente descreveu aí em cima.

Vamos juntos?

Considerações

Eu sei que você, jovem padawan, já está todo empolgado e doido para colocar a mão na massa né? Mas calma lá. Antes da gente começar a destrinchar esse modelo matemático de fato, temos que fazer algumas considerações.

Essas considerações são importantes porque são elas que vão respaldar todos os passos que tomarmos durante o nosso raciocínio, além disso, muitas das vezes fazemos considerações que podem facilitar os nossos cálculos, mas sempre sendo razoáveis, não vá se empolgar nas simplificações.

Vamos pensar juntos então em quais hipóteses assumiremos para o nosso modelo:

  1. Volume constante: isso quer dizer que a vazão de entrada é igual à vazão de saída do tanque, ou, m ˙ i = m ˙ , mantendo o volume do tanque sempre constante
  2. Mistura perfeita: como temos um tanque agitado, assumiremos que essa agitação acontece de forme perfeita, ou seja, o fluido tem as mesmas propriedades em todos os pontos do tanque, é o famoso “parâmetros concentrados”. Essa hipótese será importante para nós pois por causa dela, a temperatura da corrente de saída será a mesma da temperatura dentro do tanque.
  3. Densidade ρ e capacidade calorífica C p constantes: essas propriedades são muito importantes para a determinação do nosso modelo e assumiremos que as mesmas se comportam como constantes durante todo o processo
  4. Perdas de calor negligenciáveis: o tanque não troca energia com o meio externo.
  5. Trabalho do eixo negligenciável: o trabalho que o agitador desempenha pode ser desprezado e não afeta a temperatura do tanque.

Em geral todas as suposições que fizemos são bem razoáveis e com certeza nos ajudarão com a nossa modelagem. A não ser que esteja dito explicitamente no enunciado do seu exercício, ou que seu professor peça para você considerar essas coisas você sempre poderá assumir essas hipóteses como verdadeiras (YEEEEEY!!).

Bom, agora a gente já tem a faca e o bolo na mão, partiu?

Balanço de energia

Toda vez que estivermos trabalhando com processos térmicos devemos começar sempre pelo balanço de energia. E aí você me pergunta: “Mas toda vez?” E eu te respondo: “SIM, toda vez!”

Calma, calma, calma. Eu sei que só de ouvir balanço de energia a gente já se treme todo, mas vamos com calma que o inimigo cai. Para relembrar a expressão geral do balanço de energia:

A c ú m u l o   d e   e n e r g i a = E n t r a - S a i + G e r a d a - { C o n s u m i d a }

No nosso sistema nós temos uma corrente de entrada com uma temperatura T i então temos energia entrando, também temos uma corrente de saída com uma temperatura T , então temos uma taxa de saída de energia.

Além disso, ainda existe uma taxa de geração de energia Q ˙ que é o sistema de aquecimento do tanque, nesse caso, a serpentina. Entretanto não existe nenhuma taxa de energia sendo consumida, sendo assim, o último termo do nosso balanço é nulo, e nossa expressão fica assim:

A c ú m u l o   d e   e n e r g i a = E n t r a - S a i + G e r a d a

O nosso acúmulo de energia, pode ser descrito como a variação da energia total do sistema U ao longo do tempo:

A c ú m u l o   d e   e n e r g i a = d U d t

A energia de uma corrente é dada pela sua vazão mássica vezes a sua capacidade calorífica específica vezes a sua temperatura.

Os termos de entrada e saída podem ser escritos da seguinte forma:

E n t r a = m ˙ i c ^ p T i

S a i = m ˙ c ^ p T

Isso porque:

∆ U = m C p ∆ T

Lembrando que m ˙ i é a vazão mássica de entrada, m ˙ é a vazão mássica de saída, e m sem nada em cima é a massa dentro do tanque.

Só lembrando que os termos referentes à energia cinética, aquela relacionada à velocidade, e energia potencial, aquela que acontece quando existe um diferencial de nível, não foram considerados porque as suas variações serão praticamente nulas (e na maioria dos casos você poderá fazer essa aproximação também).

A geração de calor pode ser escrita simplesmente como Q ˙ :

G e r a d o = Q ˙

Além disso, a energia total U também pode ser substituída pela energia total específica:

U = m u ^

Sendo assim, nossa expressão de balanço de energia até agora tem essa cara aqui:

d m u ^ d t =   m ˙ i c ^ p T i - m ˙ c ^ p T + Q ˙

Para substâncias líquidas, podemos fazer a seguinte consideração:

d u ^ = d h ^ = c ^ p d T

Lembrando que todos os termos com chapeuzinho são referentes a propriedades específicas (aquelas que estão em base mássica). Não me vá esquecer isso hein.

Já estamos quase no fim do nosso balanço, ele já está bem bonitinho olha só:

m c ^ p d T d t =   m ˙ i c ^ p T i - m ˙ c ^ p T + Q ˙

Como o volume do tanque é constante, a taxa com que a nossa corrente de entrada entra tem que ser igual à taxa da saída, sendo assim a vazão de entrada é igual a vazão de saída:

m ˙ = m ˙ i

m c ^ p d T d t =   m ˙ c ^ p T i - T + Q ˙

Rearranjando nossa expressão:

d T d t = m ˙ m T i - T + Q m c ^ p ˙

Ou ainda, podemos reescrever a equação final do balanço de energia em termos de volume fazendo as seguintes substituições:

m ˙ = ρ q

m = ρ V

d T d t = q V T i - T + Q ρ V c ^ p ˙

Viu, nem doeu né?

Balanço de energia

Exercícios Resolvidos

Exercício Resolvido #1

Smith & Corripio, Princípios e Prática do Controle Automático de Processos, 3ª ed. Rio de Janeiro: LTC, 2012, pag 89, Problema 3-4. Adapatado

Considere o sensor de temperatura esboçado na figura abaixo. O bulbo e sua fonte térmica vizinha estão em uma temperatura uniforme T b ( t ) , e a vizinha está em uma temperatura uniforme T s ( t ) . A troca de calor entre a vizinhança e o bulbo é dada por:

q t = h A T s t - T b t

Onde:

q t → proporção de transferência de calor, J / s

h →   coeficiente de calor de convecção do filme, J / s m 2 º C  

A → área entre o bulbo e sua vizinhança

Considere M ,   k g , a massa do bulbo e da fonte térmica, e C v ,   J / k g º C , sua capacidade calorífica. Obtenha a função de trsnferência que descreve a a resposta de temperatura do bulbo quando a temperatura da vizinhança varia. Liste todas as suposições e desenhe o diagrama de blocos para o bulbo.

Passo 1

Antes de começar, devemos fazer nossas suposições.

Para fazer a modelagem desse bulbo, existem duas coisas que devemos considerar principalmente. Primeiro que o o bulbo se encontra a parâmetros concentrados, ou seja, a temperatura em qualquer parte do bulbo é a mesma.

Segundo, devemos considerar que não existem perdas. Toda e qualquer troca de energia acontece exclusivamente do bulbo para a vizinhança ou da vizinhança para o bulbo.

Passo 2

Vamos começar fazendo o balanço de energia para a temperatura no bulbo:

A c ú m u l o   d e   e n e r g i a = E n t r a - S a i + G e r a d a - { C o n s u m i d a }

Para esse caso, não temos nenhuma fonte de geração ou consumo de energia. Sendo assim, o balanço de enregia pode ser reduzido a:

A c ú m u l o   d e   e n e r g i a = E n t r a - S a i

A relação entre a quantidade de energia que entra e sai do nosso sistema (bulbo) já foi dada do enunciado:

E n t r a - S a i = q t = h A T s t - T b t

Logo:

A c ú m u l o   d e   e n e r g i a = h A T s t - T b t

E o Acúmulo de enercia:

A c ú m u l o   d e   e n e r g i a = d U d t = d M C v T b t d t = M C v d T b t d t

Por fim:

M C v d T b t d t = h A T s t - T b t

Passo 3

Antes de prosseguir, vamos rearranjar a EDO para conseguir trabalhar mais facilmente com ela. Sendo assim, vamos colocar todos os termos com T b ( t ) do lado esquerdo da equação.

M C v d T b t d t + h A T b t = h A T s t           ( 1 )

Além disso, precisamos ainda passar as nossas variáveis para variáveis desvio. Para isso, vamos reescrever a equação com todos as variáveis no estado inicial (vamos representar com uma barra):

M C v d T b - d t + h A T b - = h A T s -           ( 2 )

Fazendo 1 - ( 2 ) :

M C v d T b t - T b - d t + h A T b t - T b - = h A T s t - T s -

Agora, vamos definir nossas variáveis desvio:

Γ b t = T b t - T b -

Γ s t = T s t - T - s

Fazendo as substituições:

M C v d Γ b t d t + h A Γ b t = h A Γ s t             ( 3 )

Passo 4

Agora já está tudo pronto para podermos prosseguir para o próximo passo que é a aplicação da transformada de Laplace.

Aplicando Laplace em ( 3 ) teremos:

M C v s Γ b s + h A Γ b s = h A Γ s ( s )

A transformada de Laplace é uma parte muito importante da resolução desse exercício. Se você não tá com esse assunto afiado, seria bacana dar uma revisada nesse tópico!

Rearranjando:

M C v s + h A Γ b s = h A Γ s ( s )

Portanto, a função de transferência será:

Γ b s Γ s s = h A M C v s + h A

Ou:

Γ b s Γ s s = 1 M C v h A s + 1

E o diagrama de blocos:

Resposta

Γ b s Γ s s = 1 M C v h A s + 1

Exercício Resolvido #2

Smith & Corripio, Princípios e Prática do Controle Automático de Processos, 3ª ed. Rio de Janeiro: LTC, 2012, pag 89, Problema 3-5. Adapatado

Água quente a uma vazão de 2   L / m i n   (constante) e temperatura T h ( t ) é misturada com água fria a uma vazão constante de 3   L / m i n e uma temperatira constante de 20   º C . Ambos os fluxos fluem para uma banheira, mas por motivo de descuido a água está transbordando e mantendo a banheira cheia de água . O volume da banheira é de 100   L . Supondo que a água na banheira está perfeitamente misturada, deduza a equação diferencial que relaciona a temperatura da banheira T ( t ) à temperatura da água quente, T h t . Obtenha a fução de transferência Γ ( s ) / Γ h ( s ) .

Passo 1

Começando pelo clássico balanço de energia.

A c ú m u l o   d e   e n e r g i a = E n t r a - S a i + G e r a d a - { C o n s u m i d a }

Para esse caso, não temos nenhuma fonte de geração ou consumo de energia. Sendo assim, o balanço de enregia pode ser reduzido a:

A c ú m u l o   d e   e n e r g i a = E n t r a - S a i

Na nossa banheira, vamos considerar separadamente duas correntes entrando e uma corrente saindo.

Para a entrada, teremos a corrente quente a corrente fria. Sendo assim:

E n t r a = m ˙ h c p T h t + m c ˙ c p T c

Como:

m ˙ = f ρ

E n t r a = f h ρ c p T h t + f c ρ c p T c

Para a saída, iremos considerar uma corrente que é a soma das duas correntes de entrada.

s a i = f h + f c ρ c p T ( t )

Para esse problema, estamos considerando parâmetros concentrados, o que quer dizer que a temperatura na banheira é igual em todos os pontos e igual à temperatura de saída. Além disso consideraramos densidade e capacidade calorífica constantes e que não exitem perdas no sistema.

Por enquanto, estamos assim:

A c ú m u l o   d e   e n e r g i a = f h ρ c p T h t + f c ρ c p T c - f h + f c ρ c p T ( t )

Ou:

A c ú m u l o   d e   e n e r g i a = ρ c p f h T h t + f c T c - f h + f c T t

O acúmulo de energia no sistema é dado por:

A c ú m u l o   d e   e n e r g i a = d U ( t ) d t = m c p d T ( t ) d t = ρ V c p d T ( t ) d t

Juntando tudo:

ρ V c p d T ( t ) d t = ρ c p f h T h t + f c T c - f h + f c T t

V d T ( t ) d t = f h T h t + f c T c - f h + f c T t

Passo 2

Antes da gente continuar, precisamos dar uma ajeitada na casa.

Primeiramente vamos organizar a EDO passando tudo que tem T ( t ) para a esquerda da equação.

V d T ( t ) d t + f h + f c T t = f h T h t + f c T c           ( 1 )

Também precisamos passar nossa EDO para variáveis desvio. Vamos, então, reescrever a equação ( 1 ) com todas as variáveis no valor inicial (e vamos representar isso com uma barra).

V d T - d t + f h + f c T - = f h T h - + f c T c           ( 2 )

Fazendo ( 1 - ( 2 ) , teremos:

V d [ T t - T - t ] d t + f h + f c T t - T - t = f h T h t - T - h     ( 3 )

Repare que como a temperatura e a vazão da corrente fria são constantes, os termos referentes à essa corrente se anulam.

Definindo as variáveis desvio:

Γ t = T t - T - t

Γ h t = T h t - T - h

Substituindo em ( 3 ) :

V d Γ ( t ) d t + f h + f c Γ t = f h Γ h t           ( 4 )

Passo 3

Casa arrumada, podemos prosseguir. O próximo passo é a transformada de Laplace.

Aplicando Laplace em ( 4 ) teremos:

V s Γ s + f h + f c Γ s = f h Γ h ( s )

A transformada de Laplace é uma parte muito importante da resolução desse exercício. Se você não tá com esse assunto afiado, seria bacana dar uma revisada nesse tópico!

Rearranjando:

V s + f h + f c Γ s = f h Γ h ( s )

Portanto, a função de transferência será:

Γ s Γ h s = f h V s + f h + f c

Ou:

Γ s Γ h s = f h f c + f h V f h + f c s + 1

Substituindo os valores:

f h = 2   L / m i n

f c = 3   L / m i n

V = 100

Γ s Γ h s = 0,4 20 s + 1

E o diagrama de blocos:

Resposta

V d T ( t ) d t + f h + f c T t = f h T h t + f c T c

Γ s Γ h s = 0,4 20 s + 1

Exercício Resolvido #3

Elaboração própria

Considere um sistema fechado composto por duas câmaras separadas por uma parede de resitência térmica R . A câmara da direira tem temperatura T 1 ( t ) e capacidade calorífica c p 1 , e a câmara da esquerda tem temperatura T 2 e capacidade calorífica c p 2 . A câmara da direita é aquecida por uma serpentina que fornece calor a uma taxa q i . Encontre o modelo matemático que rege o sistema. Considere que os dois compartimentos estão bem misturados.

Passo 1

Para encontrar o modelo mademático que descreve o sistema, devemos encontrar o conjunto de EDO’s que governam a temperatura em cada um dos compartimentos.

Começaremos então pelo primeiro compartimento. Vamos fazer isso analisando o balanço de energia para ele:

A c ú m u l o   d e   e n e r g i a = E n t r a - S a i + G e r a d a - { C o n s u m i d a }

Os termos de geração e consumo servem para representar as taxas de calor quando temos reações químicas no sistema. Não é o caso aqui.

A c ú m u l o   d e   e n e r g i a = E n t r a - S a i

Na primeira câmara nós temos enegia entrando no sistema através da serpentina. O enunciado diz que essa energia é passada para o fluido a uma taxa q i , sendo asism:

E n t r a = q i

O primeiro compartimento também troca energia com o segundo compartimento. Pela Lei de Fourier essa troca de energia acontece da seguinte maneira:

q = 1 R T 1 t - T 2 t

Onde R é a resistência proporcionada pela parede. Sendo assim a energia que sai da primeira câmara é:

S a i = 1 R T 1 t - T 2 t

A variação de energia no primeiro compartimento também pode ser descrita como:

d U 1 d t = m c p 1 d T 1 d t

Juntando tudo:

A c ú m u l o   d e   e n e r g i a = E n t r a - S a i

Passo 2

Para o segundo compartimento, a única troca de energia que existe é com o primeiro compartimento, então:

m c p 2 d T 2 d t =   1 R T 1 t - T 2 t

Resposta

m c p 1 d T 1 d t = q i - 1 R T 1 t - T 2 t

m c p 2 d T 2 d t =   1 R T 1 t - T 2 t

Exercício Resolvido #4

Elaboração própria

Um tanque completamente fechado e cheio de um fluido com capacidade calorífica c p , densidade ρ e volume V é aquecido por uma serpentina. Um fluido que passa pela serpentina tem temperatura T s ( t ) e vazão f . Considere que a área da serpentina é igual a A e que o coefiente global de troca térmica por convecação é proporcional à vazão do fluido da serpentina. O tanque pode ser considerado bem agitado e está completamente isolado, a densidade, volume e capacidade calorífica são constantes. Encontre a função de transferência T s T s s .

Passo 1

Seguinte, vamos começar com o clássico balanço de energia:

A c ú m u l o   d e   e n e r g i a = E n t r a - S a i + G e r a d a - { C o n s u m i d a }

Nesse caso, a única fonte de energia que a gente tem é a energia proveniente da serpentina. Não temos nenhuma corrente de entrada nem de saída, nenhuma perda pro ambiente já que o tanque está bem agitado e também não temos nenhuma outra fonte de energia. Então, nosso balanço pode ser reduzido a:

A c ú m u l o   d e   e n e r g i a = E n t r a

Onde a energia que entra é a da serpentina. O tanque troca energia com a serpentina através da convecção entre o fluido do tanque e o fluido da serpentina segundo a seguinte fórmula:

q = U A [ T s ( t ) - T t ]

Onde A é a área da serpentina e U o coeficiente global de troca térmica por convecção.

O enunciado diz que U é proporcional à vazão do fluido da serpentina, logo:

U = k f

Onde k é a razão de proporcionalidade.

Logo a energia que “entra” no sistema é:

E n t r a = k f A [ T s ( t ) - T t ]

O acúmulo de energia no sistema pode ser escrito como:

A c ú m u l o   d e   e n e r g i a = d U ( t ) d t = m c p d T ( t ) d t = ρ V c p d T ( t ) d t

Logo, o balanço de energia será:

ρ V c p d T ( t ) d t = k f A [ T s ( t ) - T t ]

Rearranjando:

d T ( t ) d t = k f A ρ V c p [ T s ( t ) - T t ]

d T ( t ) d t + k f A ρ V c p T t = k f A ρ V c p T s ( t )

Passo 2

O próximo passo agora é aplicar a transformada de Laplace na nossa EDO:

s T s + k f A ρ V c p T s = k f A ρ V c p T s s

Colocando T ( s ) em evidência:

s + k f A ρ V c p T s = k f A ρ V c p T s s

Logo, a função de trasnfência T s T c s será:

T s T s s = k f A ρ V c p s + k f A ρ V c p

Ou:

T s T s s = 1 ρ V c p k f A s + 1

Resposta

T s T s s = 1 k f A ρ V c p s + 1

Exercício Resolvido #5

Seborg, Process Dynamics and Control, 4ª ed.: Wiley, 2016, pag 34, Exercício 2.8. Adapatado

Um tanque encamisado mostrado abaixo é usado para esfriar uma corrente de processo. As seguintes informações são sabidas:

  • O volume de líquido no tanque, V , e o volume de fluido refrigerante na camisa, V C , permanencem constantes. A vazão volumétrica f 0 permanece constante mas f C varia com o tempo.
  • As perdas de energia da camisa são desprezíveis.
  • Os conteúdos do tanque e da camisa podem ser considerados bem misturados e têm capacitância térmica considerável.
  • As capacitâncias térmicas da parede do tanque e da camisa são desprezíveis.
  • O Coeficiente global de troca térmica por convecção entre o líquido do tanque e o fluido refrigerante varia com a vazão na camisa:

U = K f C 0,8 ( t )

Desenvolva o modelo matemático para o sistema.

Passo 1

O exercício pede o modelo matemático que descreve o sistema, ou seja, precisamos encontrar expressões matemáticas que ilustrem o comportamento da temperatura tanto no tanque quanto na camisa.

Para fazer isso, além de todas considerações já expostas no enunciado, vamso ainda considerar que a densidade e o calor específico de ambos os fluido podem ser considerados constantes.

Vamos começar fazendo o balanço para o líquido do tanque.

A c ú m u l o   d e   e n e r g i a = E n t r a - S a i + G e r a d a - { C o n s u m i d a }

Nesse process não existe nenhuma reação que gera ou consome energia, logo o balanço de energia pode ser reduzido:

A c ú m u l o   d e   e n e r g i a = E n t r a - S a i

Além das correntes de entrada e saída, o líquido do tanque troca energia por convecção com o líquido da camisa. A quantidade de calor trocada por convecção será:

q = U A T t - T C t

Onde A é a área de troca térmica entre os dois compartimentos e U é o coeficiente de troca térmica global por convecção.

Entretanto, o enunciado diz que o valor de U varia de acordo com a quantidade de fluido na camisa da seguinte forma:

U = K f C 0,8 ( t )

Logo:

q = K f C 0,8 ( t ) A T t - T C t

Colocando tudo no balanço

A c ú m u l o   d e   e n e r g i a = f 0 ρ c p T 0 t - f ρ c p T t - K f C 0,8 ( t ) A T t - T C t

Temos um termo referente à corrente de entrada, outro referente à corrente de saída e um terceiro referete à troca térmica proporcionada pela camisa.

Porém, como o volume do tanque é constante, podemos assumir que:

f 0 = f

Sendo assim:

A c ú m u l o   d e   e n e r g i a = f ρ c p [ T 0 t - T t ] - K f C 0,8 ( t ) A T t - T C t

O termo de acúmulo de energia pode ser escrito como:

A c ú m u l o   d e   e n e r g i a = d U ( t ) d t = m c p d T ( t ) d t = ρ V c p d T ( t ) d t

Logo

ρ V c p d T ( t ) d t = f ρ c p [ T 0 t - T t ] - K f C 0,8 ( t ) A T t - T C t

Passo 2

Agora precisamos fazer o mesmo procedimento para a camisa:

A c ú m u l o   d e   e n e r g i a = E n t r a - S a i + G e r a d a - { C o n s u m i d a }

O fluido da camisa também não faz nenhuma reação, portanto:

A c ú m u l o   d e   e n e r g i a = E n t r a - S a i

Para a camisa, a montagem do balanço vai ser análoga à do tanque, uma vez que ela também apresenta uma corrente de entrada, uma corrente de saída e troca térmica por convecção com o fluido que está dentro do tanque. Sendo assim:

ρ C V C c p C d T C ( t ) d t = f C t ρ C c p C T i t - T C t + K f C 0,8 ( t ) A T t - T C t

A única diferença é que o sinal da expressão referente à troca térmica por convecção é trocado, uma vez que um fluido recebe energia e o outro fornece.

Obs: repare que a resposta encontrada foi uma EDO não linear, já que temos uma função de tempo ( f C ( t ) ) elevada a 0,8 . Caso fosse necessário aplicar transformada de Laplace para encontrar a função de transferência do processo, precisaríamos linearizar esse termo, porém, como o exercício pede apenas o modelo matemático do sistema, as EDO’s encontrada são a resposta do exercício.

Resposta

ρ V c p d T ( t ) d t = f ρ c p [ T 0 t - T t ] - K f C 0,8 ( t ) A T t - T C t

ρ C V C c p C d T C ( t ) d t = f C t ρ C c p C T i t - T C t + K f C 0,8 ( t ) A T t - T C t

Exercício Resolvido #6

Seborg, Process Dynamics and Control, 4ª ed.: Wiley, 2016, pag 34, Exercício 2.6. Adapatado

Um reator agitado completamente isolado com dois compartimentos é mostrado na figura abaixo. A ideia básica é alimentar os reagente continuamente no primeiro compartimento, onde eles serão preaquecidos pela energia liberada na reação exotérmica, que é esperado que se ocorra principalmente no segundo compartimento. A parede entre os dois compartimentos é consideravelmente fina, permitindo a troca térmica; o reator pode ser considerado perfeitamente isolado; e existe uma serpentina de resfriamento no segundo compartimento para remover o excesso de energia liberada na reação. Ambos os tanques estão completamente cheios o tempo todo.

Inicialmente serão realizados alguns testes com alimentação de um único componente (sem reação) para avaliar as características térmicas do reator.

Desenvolva o modelo matemático para esse processo sob as condições de nenhuma reação. Assuma que f 0 , T i e T C podem variar.

Passo 1

O exercício pede o modelo matemático que descreve o processo, isso quer dizer que ele quer as EDO’s que mostram como a temperatura varia no tanque. Como temos dois compartimentos precisaremos de duas EDO’s.

Começando pelo começo. Balanço de energia para o primeiro compartimento:

A c ú m u l o   d e   e n e r g i a = E n t r a - S a i + G e r a d a - { C o n s u m i d a }

O enunciado pediu para considerarmos que não existe nenhuma reação, logo, o balanço de massa para o primeiro compartimento fica:

A c ú m u l o   d e   e n e r g i a = E n t r a - S a i

Nós temos uma corrente entrando e uma corrente saindo do primeiro compartimento e além disso ainda temos troca térmica por convencção com o segundo compartimento.

A quantidade de calor trocada por convecção será:

q = U A ( T 2 - T 1 )

Onde A é a área da parede que divide os dois compartimentos e U é o coeficiente de troca térmica global por convecção do material da parede.

O nosso balanço tá assim por enquanto:

A c ú m u l o   d e   e n e r g i a 1 = f 0 t ρ c p T i t - f 1 ( t ) ρ c p T 1 ( t ) + U A T 2 t - T 1 t

Porém, o enunciado diz que ambos os compartimentos estão sempre cheio, isso quer dizer que as vazões são sempre iguais. Portanto:

f 0 ( t ) = f 1 ( t ) = f ( t )

A c ú m u l o   d e   e n e r g i a 1 = f t ρ c p T i t - f ( t ) ρ c p T 1 ( t ) + U A T 2 t - T 1 t

A c ú m u l o   d e   e n e r g i a 1 = f t ρ c p T i t - T 1 t + U A T 2 t - T 1 t

Mas como:

A c ú m u l o   d e   e n e r g i a 1 = d U 1 ( t ) d t = m 1 c p d T 1 ( t ) d t = ρ V 1 c p d T 1 ( t ) d t

Juntando tudo:

ρ V 1 c p d T 1 ( t ) d t = f t ρ c p T i t - T 1 t + U A T 2 t - T 1 t

Ou:

d T 1 ( t ) d t = f t V 1 T i t - T 1 t + U A ρ V 1 c p T 2 t - T 1 t

Passo 2

Agora podemos partir para o segundo compartimento.

A c ú m u l o   d e   e n e r g i a = E n t r a - S a i + G e r a d a - { C o n s u m i d a }

O segundo compartimento, assim como o primeiro, também não possui reação química. Portanto:

A c ú m u l o   d e   e n e r g i a = E n t r a - S a i

No segundo compartimento além as entrada e saída de energia através das correntes, e da troca térmica por convecção pela parede com o primeiro compartimento, também teremos troca térmica por convecção com a serpentina.

O calor trocado com a serpentina será:

q c = U C A C T 2 t - T C t

Onde A C é a área de troca térmica da serpentina e U C é o coeficiente de troca térmica global por convecção do material da serpentina.

Portanto, nosso balanço ficará:

A c ú m u l o   d e   e n e r g i a 2 = f 1 t ρ c p T 1 t - f 2 t ρ c p T 2 t - U A T 2 t - T 1 t - U C A C T 2 t - T C t

Mas assim como no primeiro compartimento, o segundo compartimento permanece cehio o tempo todo, o que indica que a vazão de entra é igual a vazão de saída.

f 1 ( t ) = f 2 ( t ) = f ( t )

Sendo assim:

A c ú m u l o   d e   e n e r g i a 2 = f t ρ c p T 1 t - T 2 t - U A T 2 t - T 1 t - U C A C T 2 t - T C t

Por fim:

A c ú m u l o   d e   e n e r g i a 2 = d U 2 ( t ) d t = m 2 c p d T 2 ( t ) d t = ρ V 2 c p d T 2 ( t ) d t

Juntando tudo:

ρ V 2 c p d T 2 ( t ) d t = f t ρ c p [ T 1 t - T 2 t ] - U A T 2 t - T 1 t - U C A C T 2 t - T C t

Ou:

d T 2 ( t ) d t = f t V 2 [ T 1 t - T 2 t ] - U A ρ V 2 c p T 2 t - T 1 t - U C A C ρ V 2 c p T 2 t - T C t

Resposta

d T 1 ( t ) d t = f t V 1 T i t - T 1 t + U A ρ V 1 c p T 2 t - T 1 t

d T 2 ( t ) d t = f t V 2 [ T 1 t - T 2 t ] - U A ρ V 2 c p T 2 t - T 1 t - U C A C ρ V 2 c p T 2 t - T C t

Exercício Resolvido #7

Smith & Corripio, Princípios e Prática do Controle Automático de Processos, 3ª ed. Rio de Janeiro: LTC, 2012, pag 91, Problema 3-13. Adaptado.

Considere um reator químico adiabático, exotérmico, perfeitamente misturado onde ocorre a reação A + B → C . Considere:

  • ρ → densidade dos reagentes e produtos, k m o l / m 3 , constante.
  • f → fluxo de corrente de entrada e saída, m 3 / s e g , constante.
  • T i t → temperatura de entrada, K .
  • T t → temperatura do reator, K .
  • Δ H r → calor da reação, constante e ngativo, J / k m o l .
  • c p ,   c v → Capacidades caloríficas (constantes), J / k m o l   K .
  • V → Volume do líquido no reservatório, constante, m 3 .

A cinética para a reação é expressa pela seguinte expressão de ordem zero:

r A = - k 0 e - E R T t

Onde:

k 0 → fator de frequência, k m o l / m 3   s .

E → energia de ativação, J / k m o l .

R → constnate dos gases ideais, J / k m o l   K .

Determine a função de transferência Γ ( s ) / Γ i ( s ) para o reator.

Passo 1

Além de todas as considerações que o enunciado já fez para a gente, vamos considerar também que o sistema se encontra a parâmetros concentrados e que não existe nenhum tipo de perda de energia.

Dito isso, vamos partir para o famoso balanço de energia.

A c ú m u l o   d e   e n e r g i a = E n t r a - S a i + G e r a d a - { C o n s u m i d a }

Nesse exercício nós temos uma corrente de entrada, uma corrente de saída e ainda por cima também temos uma geração de energia, isso porque acontece uma reação exotérmica no reator.

A c ú m u l o   d e   e n e r g i a = E n t r a - S a i + { G e r a d a }

Vamos escrever as expressões para cada um dos termos acima:

A c ú m u l o   d e   e n e r g i a = d U ( t ) d t = m c p d T ( t ) d t = ρ V c p d T ( t ) d t

E n t r a = m ˙ c p T i t = ρ f c p T i t

s a i = m ˙ c p T t = ρ f c p T ( t )

Para expressar a energia gerada pela reação devemos multiplicar a entalpia da reação, pela taxa e também pelo volume do reator. Logo:

G e r a d o = - Δ H r k 0 V e - E R T t V

Juntando tudo:

ρ V c p d T ( t ) d t = ρ f c p T i t - ρ f c p T ( t ) - Δ H r k 0 V e - E R T t

Passo 2

OPA, OPA, OPA. ALERTA DE PROBLEMA!

A nossa EDO ficou com um termo que não é linear. O que a gente faz quando isso acontece? Isso mesmo, lineariza hahaha.

O termo não linear éo termo relativo à energia da reação. Sendo assim, a nossa função que precisará ser linearizada é:

f T = e - E R T t

Para linearizar, nós utilizamos a linearização de Taylor:

f x = f x - + ∂ f ∂ x x - . ( x - x - ) 1 !

Logo:

f T = e - E R T - + E R T - T t - T -

Subsituindo na nossa expressão:

ρ V c p d T ( t ) d t = ρ f c p T i t - ρ f c p T ( t ) - Δ H r k 0 V e - E R T - + E R T - e - E R T - T t - T -

Passo 3

Estamos progredindo, mas a nossa EDO ainda tá muito bagunçada. Vamos aplicar variáveis desvio para tentar melhorar as coisas para o nosso lado:

ρ V c p d T ( t ) d t = ρ f c p T i t - ρ f c p T t - Δ H r k 0 V e - E R T - + E R T - e - E R T - T t - T -                       ( 1 )

Vamos reescrever a expressão ( 1 ) colocando todas as suas variáveis no estado inicial (e vamos representar essas variáveis com a barra):

ρ V c p d T - d t = ρ f c p T i - - ρ f c p T - - Δ H r k 0 V e - E R T -                       ( 2 )

Perceba que o último termo se anula porque ficamos com T - - T - = 0 .

Fazendo 1 - ( 2 ) :

ρ V c p d T t - T - d t = ρ f c p [ T i t - T i - ] - ρ f c p T t - T - - Δ H r k 0 V E R T - e - E R T - T t - T -                       ( 3 )

Vamos definir então nossas variáveis desvio:

Γ t = T t - T -

Γ i t = T i t - T i -

Finalmente:

ρ V c p d Γ ( t ) d t = ρ f c p Γ i ( t ) - ρ f c p Γ ( t ) - Δ H r k 0 V E R T - e - E R T - Γ ( t )             ( 4 )

Passo 4

Quase lá!!

Vamos dar uma organizada nessa EDO passando tudo que tem Γ ( t ) para o lado esquerdo:

ρ V c p d Γ ( t ) d t + ρ f c p Γ t + Δ H r k 0 V E R T - e - E R T - Γ ( t ) = ρ f c p Γ i ( t )

Colocando Γ t em evidência:

ρ V c p d Γ ( t ) d t + ρ f c p + Δ H r k 0 V E R T - e - E R T - Γ ( t ) = ρ f c p Γ i ( t )

Para facilitar o nosso lado, vamos definir novas constantes que agrupem todas essas constantes:

a 1 = ρ V c p

a 2 = ρ f c p + Δ H r k 0 V E R T - e - E R T -

a 3 = ρ f c p

Ficamos então com

a 1 d Γ ( t ) d t + a 2 Γ t = a 3 Γ i t               ( 5 )

Bem melhor né?

Passo 5

Para achar a função de transferência agora, só nos resta aplicar Laplace.

Aplicando Laplace na expressão ( 5 )

a 1 s Γ s + a 2 Γ s = a 3 Γ i ( s )

Colocando Γ ( s ) em evidência:

a 1 s + a 2 Γ s = a 3 Γ i ( s )

Logo a função de transferência será:

Γ s Γ i ( s ) = a 3 a 1 s + a 2

Com:

a 1 = ρ V c p

a 2 = ρ f c p + Δ H r k 0 V E R T - e - E R T -

a 3 = ρ f c p

Resposta

Γ s Γ i ( s ) = a 3 a 1 s + a 2

Com:

a 1 = ρ V c p

a 2 = ρ f c p + Δ H r k 0 V E R T - e - E R T -

a 3 = ρ f c p

Exercício Resolvido #8

Smith & Corripio, Princípios e Prática do Controle Automático de Processos, 3ª ed. Rio de Janeiro: LTC, 2012, pag 92, Problema 3-15. Adaptado.

Considere o reservatório aquecido mostrado na figura abaixo. Um fluxo de processo está sendo aquecido no reservatório por um aquecedor elétrico. A proporção da transferência calorífica, q ( t ) para o fluido de processo está relacionado ao sinal, m ( t ) , por:

q t = a m ( t )

Você pode supor que o reservatório de aquecimento está bem isolado, que o fluido está bem misturado no reservatório e que a capacidade calorífica e a densidade do fluido são constantes. Desenvolva o modelo matemático que descreva como a temperatura de entrada, T i ( t ) , o fluxo do processo, f ( t ) , e o sinal, m ( t ) , afetam a temperatura de saída T ( t ) . Depois determine as funções de transferência e esboce o diagrma de blocos.

Passo 1

Nesse exercício o enunciado foi bonzinho e já fez todas as considerações necessárias. Então vamos direto pro balanço de energia porque a gente tá sem tempo, irmão.

A c ú m u l o   d e   e n e r g i a = E n t r a - S a i + G e r a d a - { C o n s u m i d a }

Aqui, além das correntes de entrada e saída do reservatório, também teremos uma taxa de geração de energia promovido pelo aquecedor elétrico.

A c ú m u l o   d e   e n e r g i a = E n t r a - S a i + { G e r a d o }

Vamos escrever as expressões para cada um dos termos acima:

A c ú m u l o   d e   e n e r g i a = d U ( t ) d t = m c p d T ( t ) d t = ρ V c p d T ( t ) d t

E n t r a = c p m ˙ t T i t = c p ρ f ( t ) T i t

s a i = c p m ˙ ( t ) T t = c p ρ f ( t ) T ( t )

E o enunciado nos deu a expressã da energia do gerador elétrico:

G e r a d o = a m ( t )

Juntando tudo:

ρ V c p d T ( t ) d t = c p ρ f ( t ) T i t - c p ρ f ( t ) T ( t ) - a m ( t )

ρ V c p d T ( t ) d t = c p ρ f t T i t - f t T t - a m ( t )

Passo 2

E olha só. De novo caímos em uma EDO não linear. Isso acontece porque temos dois termos onde temos duas funções de tempo se multiplicando. Precisamos resolver isso.

Para fazer essa linearização, usaremos a linearização de Taylor. Quando temos um caso como esse de produto de funções, a linearização é feita da seguinte forma:

f x = h x . g ( x )

f x ≅ f x - + ∂ f ∂ h x - . h - h - 1 ! + ∂ f ∂ g x - . g - g - 1 !

Primeiro a gente escreve a função em torno do ponto onde estamos linearizando, depois nós vamos derivar a função duas vezes, uma vez em relação a cada função que compõe a função principal.

Sendo assim:

f t T i t = f - T i - + f - T i t - T i - + T i - [ f t - f - ]

E analogamente:

f t T t = f - T - + f - T t - T - + T - [ f t - f - ]

Substituindo no balanço

ρ V c p d T ( t ) d t = c p ρ f - T i - + f - T i t - T i - + T i - f t - f - - f - T - - f - T t - T - - T - f t - f - + a m t               ( 1 )

Passo 3

O próximo passo é colocar a nossa expressão em variáveis desvio. Para isso, vamos escrever a expressão ( 1 ) com todos os termos em seus estados iniciais.

ρ V c p d T - d t = c p ρ f - T i - - f - T - + a m -               ( 2 )

Olha só, a maioria dos termos se anulou porque as diferenças ficaram igual a 0 . Fazendo 1 - ( 2 ) :

ρ V c p d [ T t - T - ] d t = c p ρ f - T i t - T i - + T i - f t - f - - f - T t - T - - T - f t - f - + a m t - m -             ( 3 )

Quando fazemos 1 - ( 2 ) os termos que são puramente constantes se anulam e sobram apenas os que são função do tempo.

Vamos definir nossas variáveis desvio:

Γ t = T t - T -

Γ i t = T i t - T i -

F t = f t - f -

M t = m t - m -

Substituindo em ( 3 ) :

ρ V c p d Γ ( t ) d t = c p ρ f - Γ i t + T i - F t - f - Γ t - T - F t + a M ( t )

Rearranjando:

ρ V c p d Γ ( t ) d t = c p ρ f - Γ i t - f - Γ t + T - i - T - F t + a M ( t )

Passo 4

Agora, vamos passar tudo que depende de Γ ( t ) para a esquerda:

ρ V c p d Γ ( t ) d t + c p ρ f - Γ t = c p ρ f - Γ i t + c p ρ T - i - T - F t + a M ( t )

Show! Agora já podemos aplicar Laplace:

ρ V c p s Γ s + c p ρ f - Γ s = c p ρ f - Γ i s + c p ρ T - i - T - F s + a M ( s )

Colocando Γ ( s ) em evidência:

( ρ V c p s + c p ρ f - ) Γ s = c p ρ f - Γ i s + c p ρ T - i - T - F s + a M ( s )

Por fim:

Γ s = c p ρ f - ρ V c p s + c p ρ f - Γ i s + c p ρ T - i - T - ρ V c p s + c p ρ f - F s + a ρ V c p s + c p ρ f - M ( s )

Passo 5

Agora só nos resta esboçar o diagrama de blocos.

Como a saída Γ ( s ) depende de três entradas que estão se somando:

Resposta

ρ V c p d T ( t ) d t = c p ρ f t T i t - f t T t - a m ( t )

Γ s = c p ρ f - ρ V c p s + c p ρ f - Γ i s + c p ρ T - i - T - ρ V c p s + c p ρ f - F s + a ρ V c p s + c p ρ f - M ( s )