Variáveis de Estado: Modelagem
Teoria
A representação de modelos em variáveis de estado tem como objetivo representar os processos no domínio do tempo usando-se uma certa quantidade de equações de primeira ordem disposta de forma matricial.
📢 Clique para ver mais:
Esse modelo tem esse nome pois ele parte do princípio que conhecendo-se as entradas de um processo, e as variáveis de estado no tempo inicial, é possível conhecer as variáveis de saída em qualquer instante
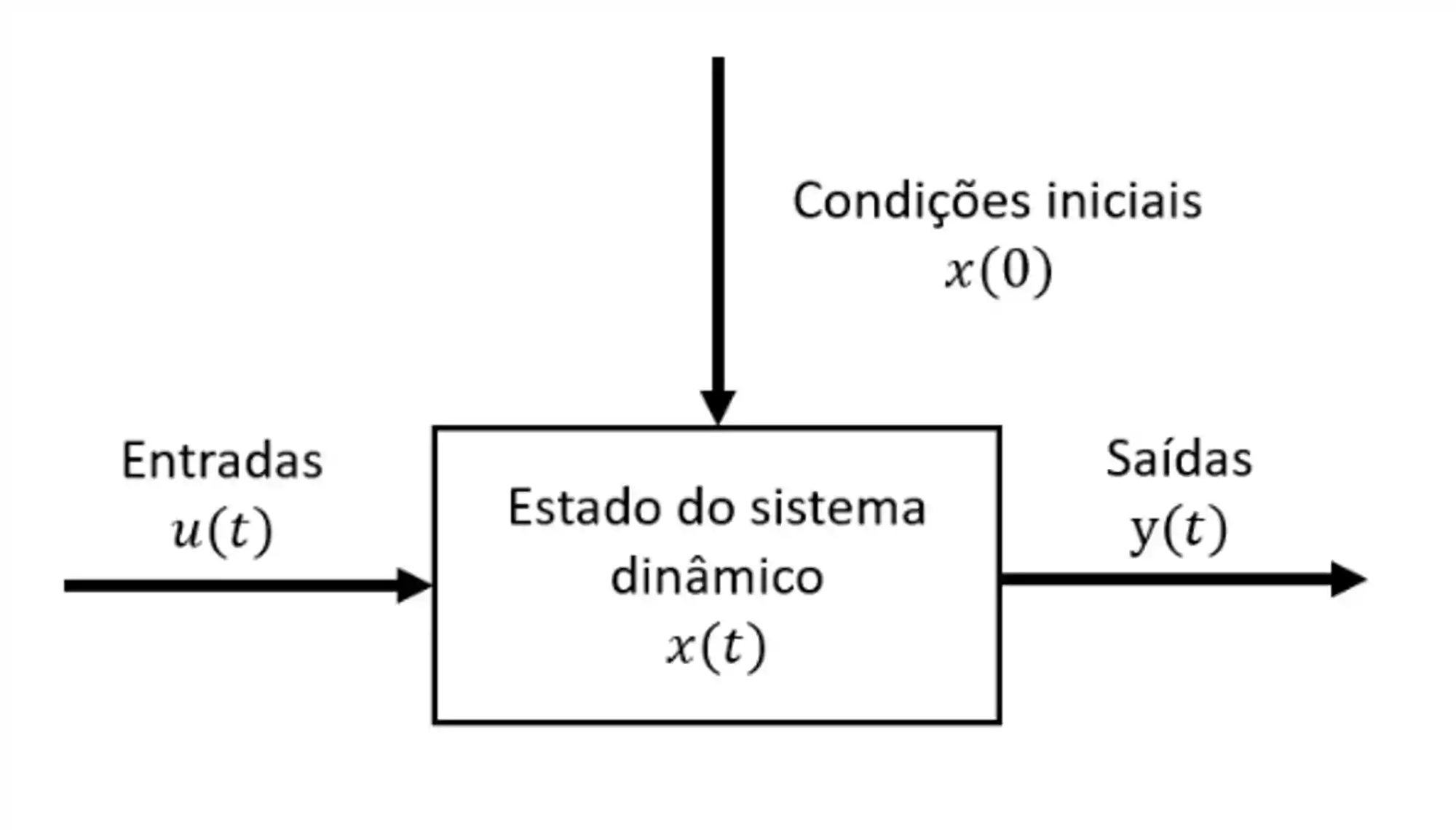
O estado de um sistema dinâmico é o menor conjunto de variáveis (as varáveis de estado) que, conhecendo-se essas variáveis no início do processo, juntamente com as entradas ao longo do processo, determina o comportamento do processo para qualquer instante futuro.
Um exemplo prático seria um tanque que está sendo enchido por uma certa corrente de entrada e queremos saber o nível desse tanque. Conhecendo o estado inicial (o nível inicial do líquido), as excitações de entrada (a vazão da entrada) e a dinâmica (a área desse tanque) será possível determinar o nível desse tanque em qualquer momento futuro!
Nessa seção, vamos denotar sempre as variáveis de entrada como
Para um sistema com duas variáveis de estado e uma entrada, a representação matricial teria o seguinte modelo:
O número de variáveis de estado necessárias para um modelo é igual ao número de equações desse modelos multiplicado pela ordem das dessa equação.
Exemplo: Modele o sistema massa-mola-amortecedor abaixo em variáveis de estado
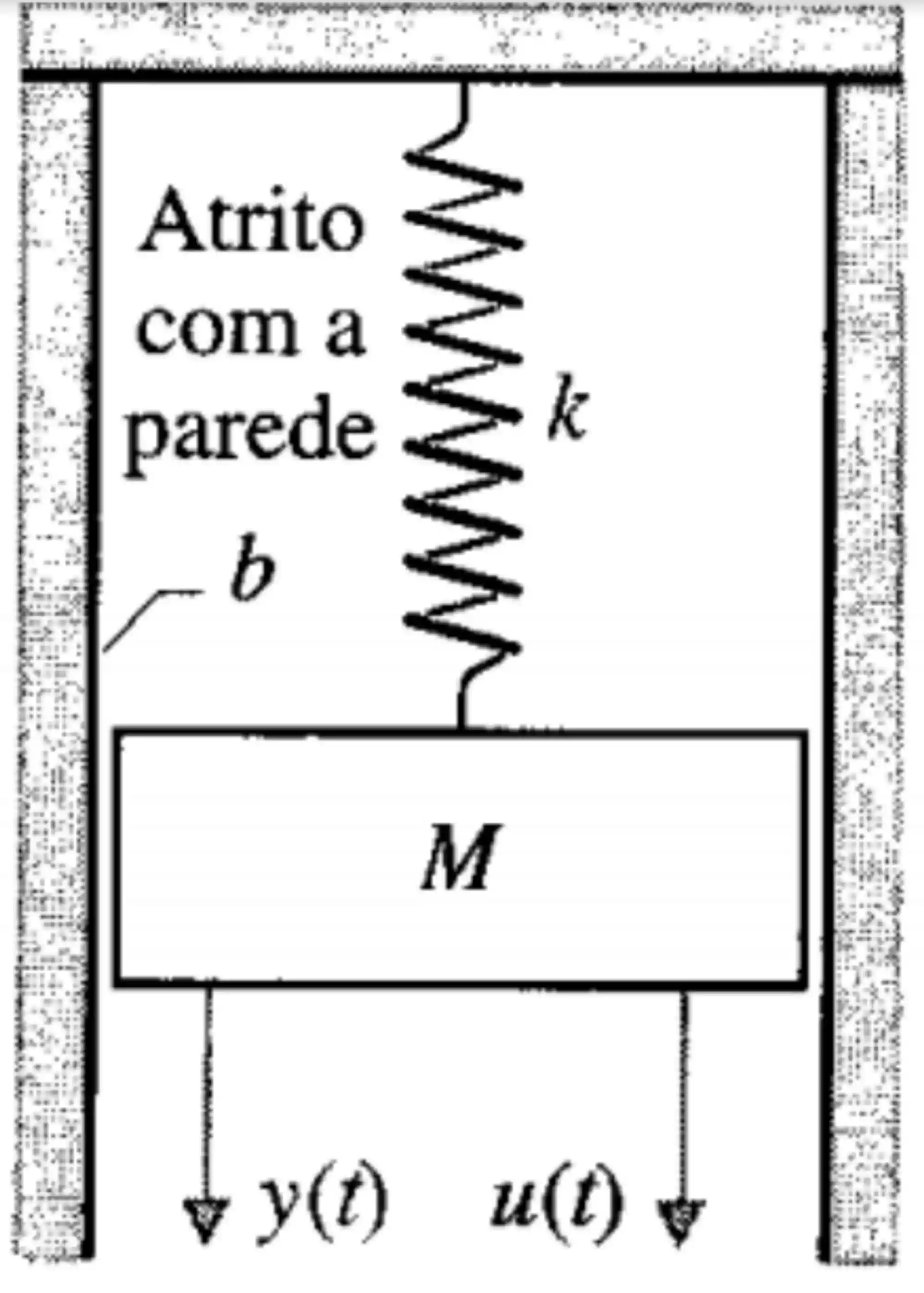
Nesse sistema,
Esse desenvolvimento foi explicado na teoria de modelos mecânicos, se você tem dúvidas de como chegar nele, seria bacana dar uma revisada lá! Como temos uma equação de segunda ordem precisamos definir duas variáveis de estado
Vamos substituir as variáveis de estado na EDO do sistema:
A gente precisa desenrolar duas equações para montar nossa matriz, uma para
Isolando
A partir das expressões acima já temos as duas equações necessárias para montar nossa matriz:
A expressão para a resposta
Como:
Prontinho! Agora vamos praticar com exercícios?
Exemplo: Modele o sistema massa-mola-amortecedor abaixo em variáveis de estado
Exercícios Resolvidos
Exercício Resolvido #1
Richard C. Dorf, Sistemas de Controle Modernos, 8ª ed., LTC, Rio de Janeiro, 2001, E3.1, pag 127
Para o circuito mostrado na figura abaixo, identificar um possível conjunto de variáveis de estado.
Passo 1
Para um determinado problema existe mais de um conjunto possível de variáveis de estado.
Para esse circuito com duas malhas, precisaremos de três variáveis de estado.
Para esse caso, nós podemos definir como a nossa entrada e a corrente , que passa pelo indutor , como uma variável de estado; a corrente , que passa pelo indutor , como outra variável de estado, e a tensão em como a terceira variável de estado.
Sendo assim:
Resposta
Exercício Resolvido #2
Richard C. Dorf, Sistemas de Controle Modernos, 8ª ed., LTC, Rio de Janeiro, 2001, E3.2, pag 127
Um sistema de acionamento do braço de um robô para uma junta de articulação pode ser representado pela equação diferencial abaixo:
Onde é a velocidade, é a posição e é a corrente do motor de controle. Expressar a equação na forma de variáveis de estado e configurar a forma matricial para .
Passo 1
Precisamos escrever a equação diferencial no modelo de variáveis de estado. A equação em questão é:
E como a velocidade é a derivada do espaço:
Temos então duas equações de ordem 1, logo, precisamos definir duas variáveis de estado .
Vamos definir a própria velocidade e posição como sendo nossas variáveis de estado:
E vamos definir a corrente do motor de controle como sendo a entrada:
Passo 2
Para escrever a EDO em um modelo de estado, precisamos escrever a equação diferencial do vetor de estado que tem a seguinte forma:
Sendo assim, precisamos encontrar uma expressão para as derivadas das nossas variáveis de estado. Para (posição) é mais fácil porque a derivada da posição é a velocidade ():
Para encontrar uma expressão para , vamos substituir as variáveis de estado na EDO:
Sendo assim, a nossa equação diferencial do vetor do estado ficará:
Passo 3
Assumindo , teremos:
Resposta
Exercício Resolvido #3
Richard C. Dorf, Sistemas de Controle Modernos, 8ª ed., LTC, Rio de Janeiro, 2001, E3.4, pag 128
Obtenha a forma matricial de variáveis de estado com variáveis de fase para um sistema com equação diferencial:
Passo 1
O primeiro passo é sempre montar definir o nosso conjunto de variáveis de estado.
O número de variáveis de estado é igual ao npumero de equações diferenciais vezes a ordem dessas equações. Nesse caso temos uma EDO de terceira ordem, então precisamos de três variáveis de estado, .
Vamos arbitrar:
Vamos substituir as variáveis de estado na EDO:
Passo 2
Para escrever a EDO em um modelo de estado, precisamos escrever a equação diferencial do vetor de estado que tem a seguinte forma:
Sendo assim, precisamos encontrar uma expressão para as derivadas das nossas variáveis de estado.
Pela definição das variáveis de estado, podemos afirmar que:
E
Para encontrar a expressão de , vamos rearranjar a nossa EDO:
Passo 3
Como já temos o nosso vetor , já podemos escrever a equação diferencial do vetor de estado:
Resposta
Exercício Resolvido #4
Richard C. Dorf, Sistemas de Controle Modernos, 8ª ed., LTC, Rio de Janeiro, 2001, E3.12, pag 128
Usar modelo em variáveis de estado para descrever o modelo do circuito abaixo. Utilize a corrente e a tensão no capacitor como variáveis de estado.
Passo 1
Vamos começar aplicando a lei das malhas no nosso circuito. Como só temos uma mlaha no circuito, só teremos uma equação:
Além disso, vamos estabelecer uma relação entre e a corrente :
Passo 2
Para escrever a EDO em um modelo de estado, precisamos escrever a equação diferencial do vetor de estado que tem a seguinte forma:
O exercício já determinou qual será o nosso vetor de variáveis de estado:
Além disso, podemos assumir que a nossa entrada será a tensão de entrada do sistema:
Sendo assim, precisamos encontrar uma expressão para as derivadas das nossas variáveis de estado.
Sunstituindo as variáveis de estado nas expressões e , teremos:
Rearranjando :
Derivando dos dois lados teremos:
Passo 3
Como já temos o nosso vetor , já podemos escrever a equação diferencial do vetor de estado:
Substituindo os valores do problema:
Resposta
Exercício Resolvido #5
Richard C. Dorf, Sistemas de Controle Modernos, 8ª ed., LTC, Rio de Janeiro, 2001, E3.13 – Adaptado- pag 128
Um sistema é descrito por duas equações diferenciais como:
Onde e são funções do tempo e é uma entrada .
- Selecionar um conjunto de variáveis de estado
- Escrever a equação diferencial matricial e especificar o elemento das matrizes
Passo 1
Bom, como e são funções do tempo, nós podemos definir essas duas variáveis como sendo o nosso vetor variáveis de estado:
Passo 2
Substituindo as variáveis de estado nas equações:
Rearranjando para obetermos e :
Passo 3
Como já temos o nosso vetor , já podemos escrever a equação diferencial do vetor de estado:
Resposta
Exercício Resolvido #6
Richard C. Dorf, Sistemas de Controle Modernos, 8ª ed., LTC, Rio de Janeiro, 2001, E3.18, pag 129
Determine a equação diferencial matricial em variáveis de estado para o circuito abaixo. Fazer , e
Passo 1
O primeiro passo é escrever as EDO’ que governam o sistema.
Para encontrar essas EDO’s, vamos usar a lei das malhas. Vamos escrever uma equação para a malha onde passa a corrente e outra para onde passa a corrente :
Além disso, também sabemos que a corrente que passa no capacitor é igual à soma das correntes e :
Passo 2
Para escrever a equação diferencial matricial em um modelo de estado, precisamos escrever a equação diferencial do vetor de estado que tem a seguinte forma:
Como temos três EDO’s de primeira ordem, precisamos de três variáveis de estado. Para nossa sorte, o enunciado já determinou qual será o nosso vetor de variáveis de estado:
Além disso, para esse circuito, temos duas entradas:
Vamos substituir tudo isso nas equaões , e :
Passo 3
Para escrever a equação diferencial em variáveis de estado na forma matricial, precisamos encontrar o vetor .
Rearranjando as equações , e :
Passo 4
Com as equações , e , podemos obter nosso vetor e assim, escrever a equação diferencial em variáveis de estado na forma matricial.
Resposta
Exercício Resolvido #7
Richard C. Dorf, Sistemas de Controle Modernos, 8ª ed., LTC, Rio de Janeiro, 2001, E3.15 - pag 128
Considere-se o caso de duas massas conectadas como mostrado na figura abaixo. O atrito de deslizamento de cada massa tem constante . Determinar a equação diferencial de estado na forma matricial.
Passo 1
Vamos escrever a equação de equilíbrio de forças para amabs as massas. Para a primeira:
Analogamente para a segunda:
Se você tover dúvida em como chegar nessas equações, seria legal dar uma revisada no conteúdo de modelos mecânicos.
Passo 2
Temos duas equações de segunda ordem, ou seja, precisamos de quatro variáveis de estado. Vamos definir a posição e a velocidade de cada uma das massas como sendo as nossas variáveis de estado:
Substituindo nas equaçõs acima:
Passo 3
Para escrever a equação diferencial de estado na forma matricial precisamos determinar o nosso vetor .
Como a velocidade é a derivada da posição, já sabemos que:
E, a paritr das equações e , temos:
Passo 4
A partir das equações , , e podemos montar nossa equação matricial:
Resposta
Exercício Resolvido #8
Richard C. Dorf, Sistemas de Controle Modernos, 8ª ed., LTC, Rio de Janeiro, 2001, E3.16 - pag 129
Dois carros com atrito de rolamento insignificante são conectados como mostrado na figura abaixo. A força de entrada é . Determina a equação diferencial em variáveis de estado na forma matricial.
Passo 1
Vamos escrever a equação de equilíbrio de forças para amabs as massas. Para a primeira:
Analogamente para a segunda:
Se você tover dúvida em como chegar nessas equações, seria legal dar uma revisada no conteúdo de modelos mecânicos.
Passo 2
Temos duas equações de segunda ordem, ou seja, precisamos de quatro variáveis de estado. Vamos definir a posição e a velocidade de cada uma das massas como sendo as nossas variáveis de estado:
Substituindo nas equaçõs acima:
Passo 3
Para escrever a equação diferencial de estado na forma matricial precisamos determinar o nosso vetor .
Como a velocidade é a derivada da posição, já sabemos que:
Vamos rearranjar as equações e para enxontrar e .
Rearranjando :
Rearranjando (2):
Passo 4
A partir das equações , , e podemos montar nossa equação matricial: