Exercícios de Modelos térmicos - Lista de Exercícios Resolvida
Questão 1
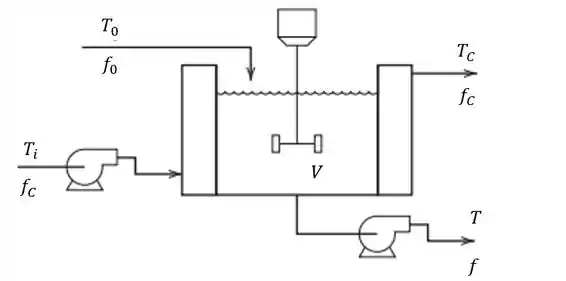
Um tanque encamisado mostrado abaixo é usado para esfriar uma corrente de processo. As seguintes informações são sabidas:
- O volume de líquido no tanque, , e o volume de fluido refrigerante na camisa, , permanencem constantes. A vazão volumétrica permanece constante mas varia com o tempo.
- As perdas de energia da camisa são desprezíveis.
- Os conteúdos do tanque e da camisa podem ser considerados bem misturados e têm capacitância térmica considerável.
- As capacitâncias térmicas da parede do tanque e da camisa são desprezíveis.
- O Coeficiente global de troca térmica por convecção entre o líquido do tanque e o fluido refrigerante varia com a vazão na camisa:
Desenvolva o modelo matemático para o sistema.
Questão 2
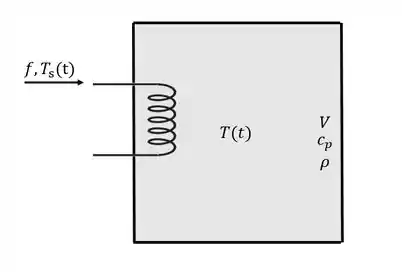
Um tanque completamente fechado e cheio de um fluido com capacidade calorífica , densidade e volume é aquecido por uma serpentina. Um fluido que passa pela serpentina tem temperatura e vazão . Considere que a área da serpentina é igual a e que o coefiente global de troca térmica por convecação é proporcional à vazão do fluido da serpentina. O tanque pode ser considerado bem agitado e está completamente isolado, a densidade, volume e capacidade calorífica são constantes. Encontre a função de transferência .
Questão 3
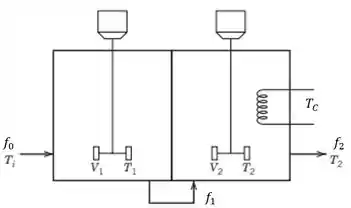
Um reator agitado completamente isolado com dois compartimentos é mostrado na figura abaixo. A ideia básica é alimentar os reagente continuamente no primeiro compartimento, onde eles serão preaquecidos pela energia liberada na reação exotérmica, que é esperado que se ocorra principalmente no segundo compartimento. A parede entre os dois compartimentos é consideravelmente fina, permitindo a troca térmica; o reator pode ser considerado perfeitamente isolado; e existe uma serpentina de resfriamento no segundo compartimento para remover o excesso de energia liberada na reação. Ambos os tanques estão completamente cheios o tempo todo.
Inicialmente serão realizados alguns testes com alimentação de um único componente (sem reação) para avaliar as características térmicas do reator.
Desenvolva o modelo matemático para esse processo sob as condições de nenhuma reação. Assuma que , e podem variar.
Questão 4
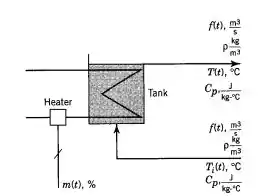
Considere o reservatório aquecido mostrado na figura abaixo. Um fluxo de processo está sendo aquecido no reservatório por um aquecedor elétrico. A proporção da transferência calorífica, para o fluido de processo está relacionado ao sinal, , por:
Você pode supor que o reservatório de aquecimento está bem isolado, que o fluido está bem misturado no reservatório e que a capacidade calorífica e a densidade do fluido são constantes. Desenvolva o modelo matemático que descreva como a temperatura de entrada, , o fluxo do processo, , e o sinal, , afetam a temperatura de saída . Depois determine as funções de transferência e esboce o diagrma de blocos.
Questão 5
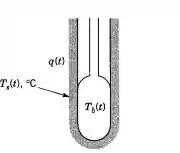
Considere o sensor de temperatura esboçado na figura abaixo. O bulbo e sua fonte térmica vizinha estão em uma temperatura uniforme , e a vizinha está em uma temperatura uniforme . A troca de calor entre a vizinhança e o bulbo é dada por:
Onde:
proporção de transferência de calor,
coeficiente de calor de convecção do filme,
área entre o bulbo e sua vizinhança
Considere , a massa do bulbo e da fonte térmica, e , sua capacidade calorífica. Obtenha a função de trsnferência que descreve a a resposta de temperatura do bulbo quando a temperatura da vizinhança varia. Liste todas as suposições e desenhe o diagrama de blocos para o bulbo.
Ver solução completaQuestão 6
Considere um reator químico adiabático, exotérmico, perfeitamente misturado onde ocorre a reação . Considere:
- densidade dos reagentes e produtos, , constante.
- fluxo de corrente de entrada e saída, , constante.
- temperatura de entrada, .
- temperatura do reator, .
- calor da reação, constante e ngativo, .
- Capacidades caloríficas (constantes), .
- Volume do líquido no reservatório, constante, .
A cinética para a reação é expressa pela seguinte expressão de ordem zero:
Onde:
fator de frequência, .
energia de ativação, .
constnate dos gases ideais, .
Determine a função de transferência para o reator.
Ver solução completaQuestão 7
Água quente a uma vazão de (constante) e temperatura é misturada com água fria a uma vazão constante de e uma temperatira constante de . Ambos os fluxos fluem para uma banheira, mas por motivo de descuido a água está transbordando e mantendo a banheira cheia de água . O volume da banheira é de . Supondo que a água na banheira está perfeitamente misturada, deduza a equação diferencial que relaciona a temperatura da banheira à temperatura da água quente, Obtenha a fução de transferência .
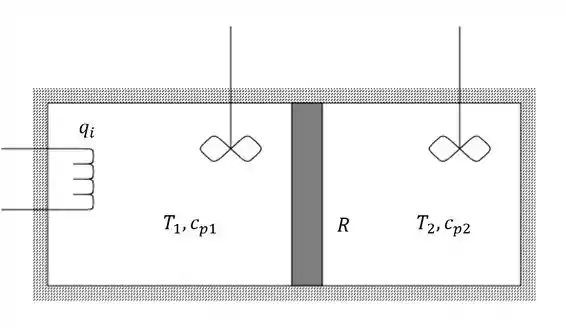
Ver solução completaQuestão 8
Considere um sistema fechado composto por duas câmaras separadas por uma parede de resitência térmica . A câmara da direira tem temperatura e capacidade calorífica , e a câmara da esquerda tem temperatura e capacidade calorífica . A câmara da direita é aquecida por uma serpentina que fornece calor a uma taxa . Encontre o modelo matemático que rege o sistema. Considere que os dois compartimentos estão bem misturados.