Sistemas de primeira ordem
Teoria
Introdução
Neste tópico vamos aprender um pouco sobre sistemas de primeira ordem, ou seja, sistemas cujas funções de transferências são derivadas de uma EDO de primeira ordem.
A expressão geral de uma função de transferência de primeira ordem é essa:
Onde:
- Variável de saída
- Variável de entrada
- Ganho do processo
- Constante de tempo de primeira ordem
O ganho do processo é a razão entra a variação da variável de saída em relação à variável de entrada. Dessa forma:
Já a constante de tempo, , caracteriza o tempo de resposta de um sistema. Maiores constantes de tempo indicam um sistema mais lento, enquanto constantes de tempos baixas indicam processos mais ágeis, ou seja, que se aproximam do valor final mais rapidamente.
Obtendo a função de transferência de primeira ordem
Beleza, mas como a gente chega nessa expressão? Para responder isso, vamos lembrar do nosso exemplo do tanque de nível que vimos no tópico de modelos fluídicos.
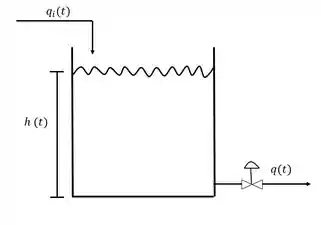
Para relembrar: nós queremos controlar o nível do tanque em relação a variações na vazão de entrada . Após fazermos a modelagem, linearização e introduzirmos as variáveis desvio, nossa EDO ficou da seguinte forma:
Repara que essa é uma EDO de primeira ordem, o que indica que a função de transferência resultante será uma função de transferência de primeira ordem. Vamos conferir?
Para facilitar nossa vida, vamos chamar , para não termos que ficar escrevendo esse termo grande sempre. Então:
Assim que o nosso modelo já está prontinho (linearizado e em variáveis desvio), o próximo passo é aplicar a transformada de Laplace na EDO:
Lembrando que a transformada de Laplace da derivada primeira de uma função é sempre vezes a transformada da própria função. Além disso, estamos considerando que todos os termos nos estados iniciais são iguais a , porque introduzimos as variáveis de desvio e também por que essa é uma das condições para se ter uma função de transferência, lembra?
Agora passamos os termos com para a esquerda e isolamos ele:
Rearranjando:
OPA, tá muito parecido com o modelo padrão que eu coloquei ali em cima né, mas repara que na equação padrão de primeira ordem, sempre aparece um no denominador, então nós vamos dividir o numerador e o denominador por para forçar esse 1 a aparecer.
Agora sim temos a nossa função de transferência de primeira ordem no modelo padrão. Colocar ela no jeitinho que o modelo manda é fundamental para que a gente consiga fazer a comparação e encontrar os parâmetros. Nesse caso
Resposta ao degrau
Como vimos, a equação característica para a função de transferência de primeira ordem é:
Sendo, assim a expressão para a resposta (variável de saída) do sistema é:
A variável de saída , depende diretamente da entrada , e portanto, pode reagir de diferentes formas para diferentes variáveis de entrada .
Imagine que no exemplo do tanque de nível, em um dado momento, a vazão de entrada passou de para . Esse tipo de variação da variável de entrada, onde acontece uma mudança pontual no valor da variável é chamado de degrau. Nesse caso, dizemos que ocorreu uma perturbação degrau de amplitude (ou magnitude) .
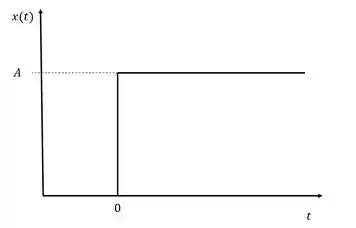
A transformada de Laplace para a perturbação degrau é:
Onde é a amplitude do degrau.
Portanto, a expressão de fica:
Fazendo a transformada inversa para voltar ao domínio do tempo:
Antes de fazer a transformada inversa, primeiramente devemos separar a equação em frações parciais, caso você não se lembre como fazer esse processo, seria bacana dar uma revisada na aula de transformadas de Laplace e suas inversas.
Tempo de subida e tempo de acomodação
Vimos ali em cima que a entrada degrau nos dá uma resposta no domínio tempo do tipo:
Essa resposta, devido ao termo exponencial, gera um gráfico mais ou menos assim:
Devido a esse comportamento exponencial da resposta, existem duas constantes que são muito importantes para o estudo das funções de primeira ordem com entrada degrau.
A primeira delas é o tempo de subida (esse ‘r’ é de ‘rising’), que se refere ao tempo que a resposta leva para ir de a . Ela pode ser definida matematicamente como:
Além disso, temos ainda o tempo de acomodação () (o ‘s’ é de settling), que é o tempo para a resposta alcance uma faixa limite da resposta final. Esse valor pode mudar dependendo da faixa que for estipulada.
Por exemplo, se a exigência for que a resposta atinja uma faixa menor que da resposta final, esse valor pode ser aproximado como:
Agora, se a sua faixa for mais restrita, menor que por exemplo, o tempo de acomodação será:
Obs: esses termos podem aparecer com outras nomenclaturas ou outras simbologias dependendo da referência que o seu professor usa ;)
Resposta à rampa
Quando a variável de entrada começa a variar linearmente a partir de um estado inicial, chamamos essa perturbação de rampa:
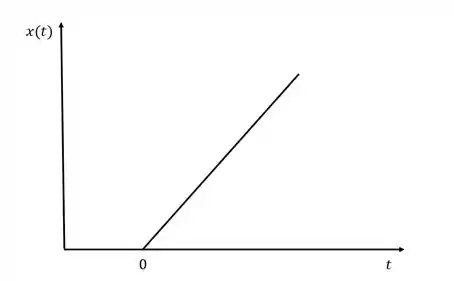
Para a rampa, a transformada de Laplace é:
Onde é a inclinação da rampa.
Sendo assim, a resposta fica:
Fazendo a inversa:
Além da rampa e do degrau, existem ainda outros tipos de perturbação, como o impulso e a perturbação senoidal, entretanto esses tipos de perturbação não são tão comuns quanto o degrau e a rampa e por isso nós focamos apenas nessas duas aqui, mas fique ligado que você pode encontrar essas outras por aí também.
Resposta ao degrau
Tempo de subida e tempo de acomodação
Resposta à rampa
Exercícios Resolvidos
Exercício Resolvido #1
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Problema 4.2. Adaptado
Obtenha a resposta de saída, , para cada um dos sistemas mostrados abaixo. Além disso, obtenha a constante de tempo, o tempo de subida e o tempo de acomodação para uma faixa menor que da resposta final para cada caso.
Passo 1
Esse é aquele tipo clássico de questão onde a gente tem uma função de transferência e precisamos compará-la com a função de transferência padrão para encontrar nossos parâmetros.
A função de transferência padrão de primeira ordem é assim:
Precisamos então colocar a nossa função de transferência nessa forma. Para isso, o termo independente de s no denominador precisa ser 1. Então dividimos nossa função de transferência em cima e embaixo por ele. Para o item (a):
Passo 2
Agora já podemos fazer a comparação. No item (a):
Agora que temos nossa constante de tempo, , podemos calcular o tempo de subida, , e o tempo de acomodação, .
Passo 3
Para encontrar a resposta devemos calcular a transformada de Laplace inversa de
Porém, a gente já tem um modelinho pronto pra funções de primeira ordem com entrada degrau:
Então, só precisamos substituir os valores de ganho, constante de tempo e de amplitude do degrau na equação:
Passo 4
Fazendo o mesmo para o item (b)
Comparando com a equação padrão:
Passo 5
Os tempos de subida e acomodação serão:
E a resposta :
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Elaboração própria
Encontre a função de transferência para a equação abaixo e determine e .
Passo 1
Como a gente tem a EDO no domínio tempo, o primeiro passo será aplicar transformada de Laplace em nossa equação, já que função de trsnferências sempre serão representadas no domínio s.
Vamos aplicar a transformada em cada termo:
Reescrevendo nossa equação agora em termos de s:
Passo 2
Agora devemos rearranjar nossa equação para que ela fique com cara de função de transferência. Colocando em evidência:
Passo 3
Agora já temos nossa função de trsnferência:
E para achar o ganho, , e a constante de tempo, , precisamos comparar a noss FT com a FT padrão de primeira ordem:
Para isso, nós precisamos fazer aparecer aquele 1 no nosso denominador, então vamos dividir toda nossa FT por três:
Então, comparando com a FT padrão:
Resposta
Exercício Resolvido #3
Prof Luiz de França Neto, Introdução ao controle de processos químicos, Santos – SP, 2017, Exercício 3.1, pag. 20
A figura abaixo representa a resposta da variável de saída a uma perturbação degrau de magnitude de unidades na variável de entrada de um processo, a partir de um instante em que o processo estava em regime permanente. Com base nessas informações defina a função de transferência do processo.
Passo 1
O exercício pede que a gente determine a função de transferência do processo, e pela cara do gráfico já dá pra matar que é uma função de transferência de primeira ordem.
A função de transferência de primeira ordem padrão é desse jeitinho aqui ó:
Então, para determinar nossa F.T. devemos encontrar os valores dos parâmentros e .
Passo 2
Vamos focar primeiramente no nosso ganho .
O ganho, por definição é a razão entre a variação da variável de saída sobre a variação da variável de entrada.
Pelo nosso gráfico podemos ver que a variável de saída vai de até , e o enunciado nos diz que a variação na entrada foi de magnitude . Então:
Passo 3
Vamos partir então para a determinação da nossa contante de tempo .
Uma das propriedades das constantes de tempos em funções de transferência de primeira ordem, é que quando , resposta se encontra em aproximadamente da variação total.
Então para encontrar o nosso precisamos encontrar o tempo em que:
Esse valor de é atingido quando , sendo assim:
Resposta
Exercício Resolvido #4
Prof Luiz de França Neto, Introdução ao controle de processos químicos, Santos – SP, 2017, Exercício 3.2, pag. 21. Adaptado
Sejam as funções de transferência abaixo:
Determine:
O ganho e a constante de tempo de cada sistema;
O valor final no estado estacionário após uma perturbação degrau unitário para cada sistema.
Passo 1
O primeiro item pede que a gente calcule os valores de e para cada sistema. Para isso, precisamos comparar nossas funções de transferência com a função de transferência padrão de primeira ordem.
Para fazer essa comparação precisamos fazer aparecer aquele no denominador da F.T.
Em , vamos dividir o numerador e o denominador por , então:
A função de transferência já está no formato que a gente precisa, então não vamos mexer em nada nela.
A tem um no denominador, então vamos dividir tanto o numerado quanto o denominador para chegar naquele que a gente precisa.
Passo 2
Agora que já modificamos nossas funções pra elas ficarem no modelo padrão, a gente só precisa comparar elas com a F.T. padrão ara encontrar nossos parâmetros.
Passo 3
Para determinar o valor do estado estacionário, devemos utilizar o teorema da valor final:
Calma, te explico.
Esse teorema diz que o valor no infinito de uma função é igual ao limite de de sua trnsformada vezes .
Como a entrada é do tipo degrau unitário também devemos multiplicar nossas funções de transferência por . Entçao, para :
Para
Para :
Obs: podemos perceber que o valor final para as funções de primeira ordem com entrada degrau sempre será o ganho multiplicado pela amplitude do degrau.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Prof Luiz de França Neto, Introdução ao controle de processos químicos, Santos – SP, 2017, Exercício 3.3, pag. 21. Adaptado
Um processo apresenta uma função de transferência de 1ª ordem entre sua saída e sua entrada , expressas em variáveis desvio. Admitindo-se que uma perturbação do tipo degrau unitário foi aplicada em , em a constante de tempo pode ser obtida pelo intervalo de tempo decorrido entre e um valor definido de tempo posterior. Esse tempo posterior corresponde ao momento para o qual a saída sofreu que porcentagem da variação total?
Passo 1
Vamos analisar tudo que o enunciado nos fala e tentar relacionar com o que já sabemos.
A primeira coisa que ele nos diz, é que a função de transferência entre e é uma função de transferência de primeira ordem. Portanto:
Além disso, tambémdiz que a foi aplicado uma variação degrau unitário em . Então:
Passo 2
Se expandirmos essa expressão em frações parciais, e aplicarmos a transformada inversa, termos:
Repare que se for muito grande, e essa será a variação máxima que a variável de saída sofrerá.
Passo 3
O exercício nos pergunta qual será a porcentagem da variação máxima que a variável terá sofrido quando . Sendo assim:
Sendo assim, a contante de tempo pode ser obtida através do intervalo de tempo entre e o ponto em que a resposta tenho sofrido uma variação de da variação máxima.
Resposta
da variação máxima
Exercício Resolvido #6
Concurso público – Edital nº 05/2014 – Reitoria/IFRN – FUNCERN – Questão 38
Considere um sistema de primeira ordem cuja relação entrada-saída é dada por:
Com relação ao desempenho desse sistema, é correto afirmar que
a) Se a entrada é em degrau, a resposta alcança mais de 98% do seu valor final quando .
b) Quanto menor for o valor de , mais rapidamente a resposta ao impulso unitário do sistema decai para zero.
c) Quanto maior o valor de , menor o erro estacionário ao seguir uma entrada em rampa.
d) Quando , a resposta alcança o valor 63,2% da sua variação total, caso a entrada seja em degrau.
Passo 1
Antes de analisarmos item a item, vamos pegar nussa função de transferência e coloca-la no nosso modelo padrão, para isso, vamos dividir numerador e denominador por .
Sendo assim:
Passo 2
Vamos analisar item a item então.
No item (a), o enunciado diz que para uma entrada dedegrau, a resposta alcança do valor final em , ou seja, .
Nós sabemos que para a entrada degrau, a nossa função no tempo ficará da seguinte forma:
Vamos substituir então , e ver o que encontramos:
Portanto, a afirmação é incorreta.
Passo 3
Na alternativa (b) o enunciado afirma que quanto menor for mais rapidamente a resposta cai para para a entrada impulso unitário.
A entrada impulso unitário tem função de transferência igual a , ou seja, . Sendo assim:
Fazendo a inversa:
Sendo assim, quanto maior for o valor de , mais rapidamente a resposta se aproximará de , e portanto, a afirmação é incorreta.
Passo 4
O item (c) afirma que quanto maior o valor de , menor será o erro no estado estado estacionário para a entrada rampa.
Para a entrada rampa, nós vimos na nossa teoria que:
Onde é o ganho e é a inclinação da rampa.
Podemos perceber que no estado estacionário (tempo infinito), o primeiro termo da expressão tenderá a , e a resposta , será diretamente proporcional ao ganho .
Como , quanto maior for o valor de , menor será o ganho da função de transferência, e consequentemente, menor será o erro no estado estacionário.
Portanto essa alternativa é verdadeira.
Passo 5
A última alternativa diz que para a entrada rampa, a resposta atinge do valor final quando .
Pela expressão para a entrada degrau que vimos no passo 2, podemor perceber que a resposta atinge esse valor quando :
Como, no nosso exemplo, , essa afirmativa também está incorreta.
Resposta
c) Quanto maior o valor de , menor o erro estacionário ao seguir uma entrada em rampa.
Exercício Resolvido #7
Elaboração própria
Um manômetro leva segundos para indicar da resposta de um degrau unitário. Calcule a contanste de tempo do manômetro sabendo que o mesmo se comporta como uma função de primeira ordem.
Passo 1
Como o nosso manômetro tem comportamento de primeira ordem:
Nesse caso, a variável seria a pressão indicada pelo manômetro, e , a pressão real. Como foi feita uma perturbação do tipo degrau unitário:
Expandindo em frações parciais e fazendo a inversa:
Passo 2
O exercício nos pede a constante de tempo sabendo que em segundos, atingiu-se da resposta total. A resposta total é igual a , para conferir isso basta fazer o limite de t indo a infinito na nossa expressão de .
Sendo assim:
Resposta
Exercício Resolvido #8
Elaboração própria
Um termômetro que funciona como uma função de transferência leva segundos para indicar da resposta a um degrau.
Quanto tempo o termômetro levará para indicar da resposta final?
Passo 1
Como o nosso termômetro tem comportamento de primeira ordem e a entrada é do tipo degrau:
Calculando a inversa:
Passo 2
O enunciado nos diz que em , o termômetro indica da resposta final, com esses dados, nós podemos calcular :
Passo 3
Sendo assim, nossa equação de fica da seguinte forma:
Para da resposta final: