Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Critério de Nyquist

Ver Todos os Exercícios

Teoria

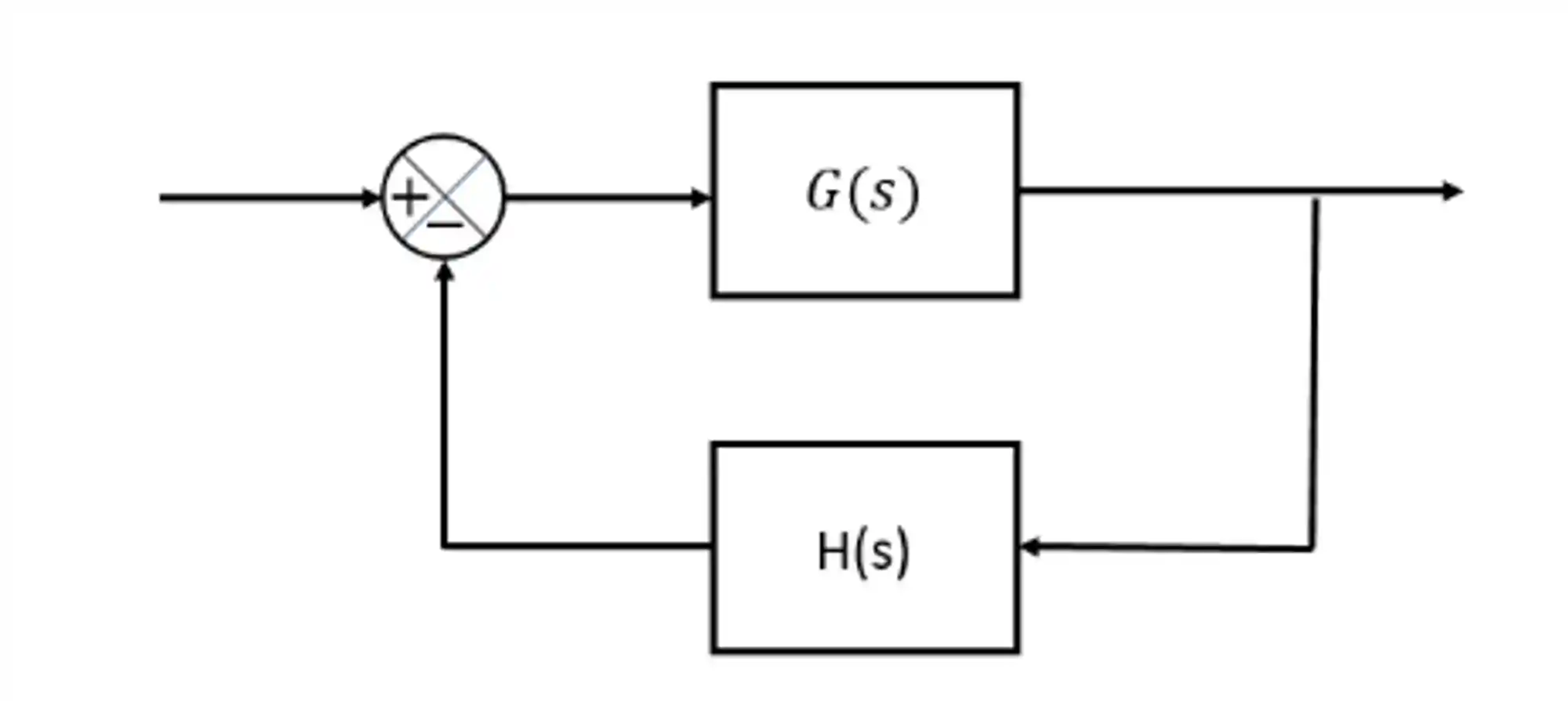
O Critério de Nyquist usa a expressão da malha aberta para determinar a estabilidade de um sistema.

Sistema em malha fechada
Sistema em malha fechada

📢 Clique para saber mais:

Para esse caso a função de transferência em malha fechada será:

E em malha aberta, será:

Para aplicar o critério de Nyquist, nós usaremos a expressão para a função de transferência em malha aberta, para determinar o número de polos da função de transferência em malha fechada, , que se encontram no semiplano direito. Dessa forma, poderemos saber a estabilidade em malha fechada através da função de transferência em malha aberta.


Para que seja possível determinar o número de polos no semiplano positivo da função de transferência em malha fechada, a função de transferência em malha aberta deverá passar por um processo chamado mapeamento de contorno. Esse mapeamento vai nos gerar diagramas chamados de Diagramas de Nyquist. O diagrama genérico para uma função em malha aberta com dois polos negativos está representado abaixo.

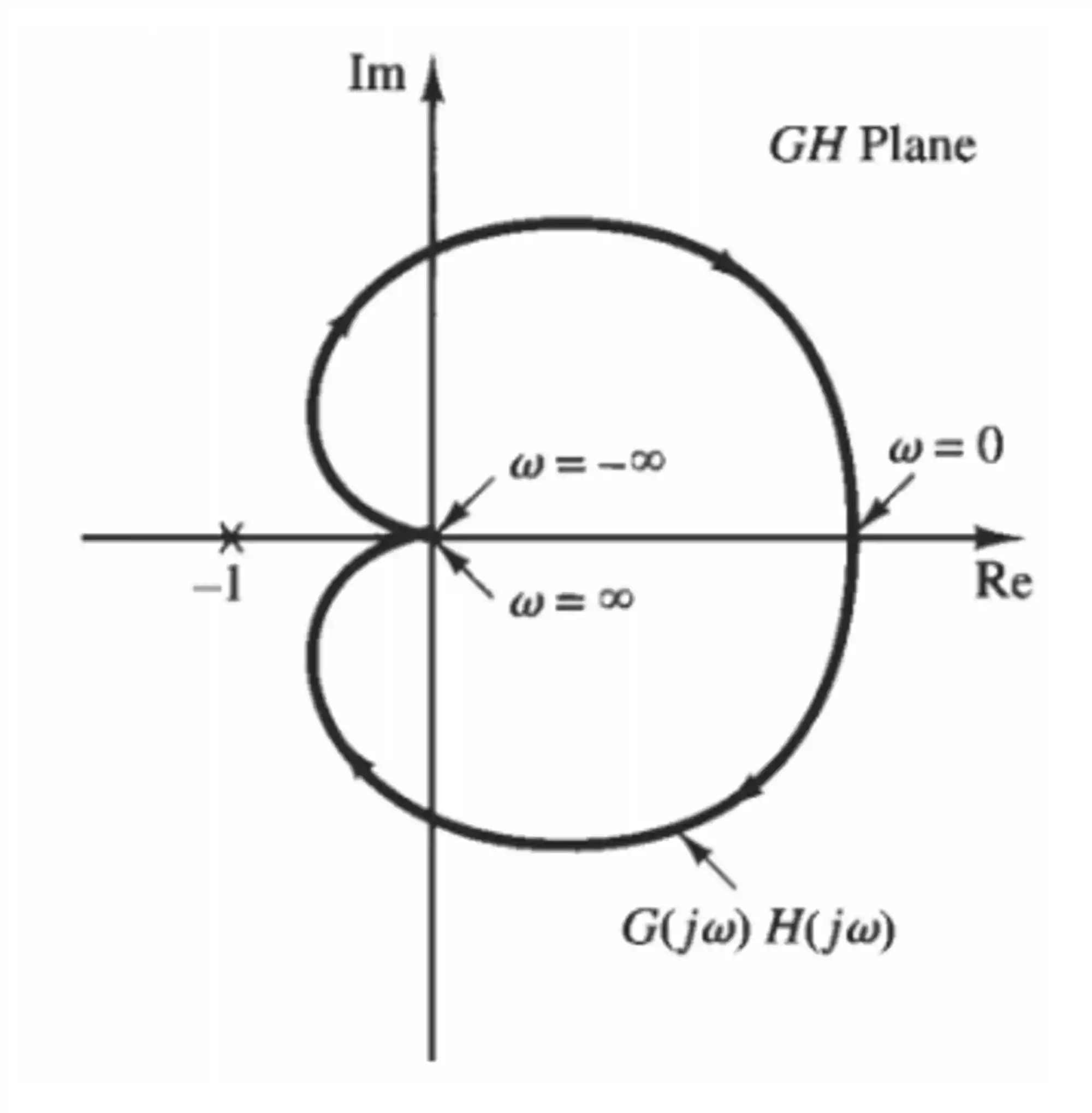
Diagrama de Nyquist
Diagrama de Nyquist

Como Fazer o Diagrama de Nyquist: Mapeamento de Contorno

Para obter nosso Diagrama de Nyquist nós precisaremos submeter a nossa equação de malha aberta a um processo chamado mapeamento de contorno. Mapeamento é quando substituímos um número complexo numa função.


Por exemplo, dada a função:

E fazemos a seguinte substituição:

Então temos:

Então dizemos que está mapeado em . O mapeamento de contornos acontece quando substituímos todo um conjunto de números em uma função e obtemos um outro conjunto.

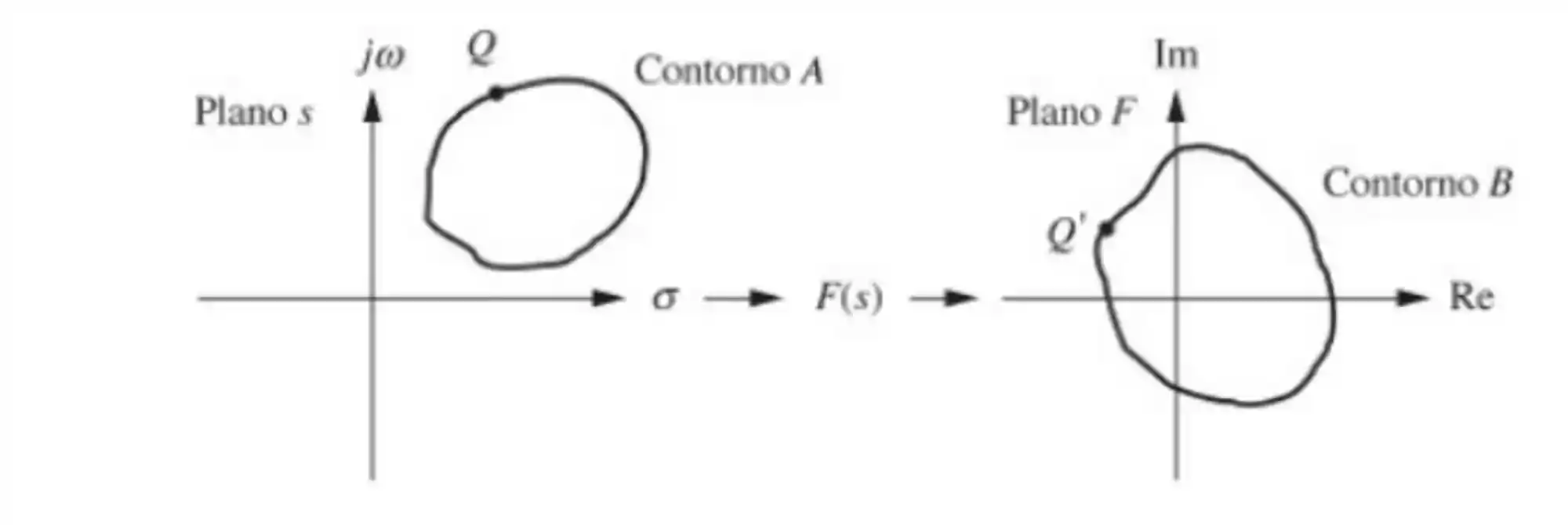
Mapeamento do contorno
Mapeamento do contorno

Na imagem acima, o contorno foi mapeado através da função no contorno .

-Ok, mas como tudo isso se aplica no Critério de Nyquist?


Para obter o diagrama de Nyquist que é a peça fundamental para determinarmos a estabilidade do sistema, precisaremos mapear o semiplano positivo através da função de transferência de malha aberta.

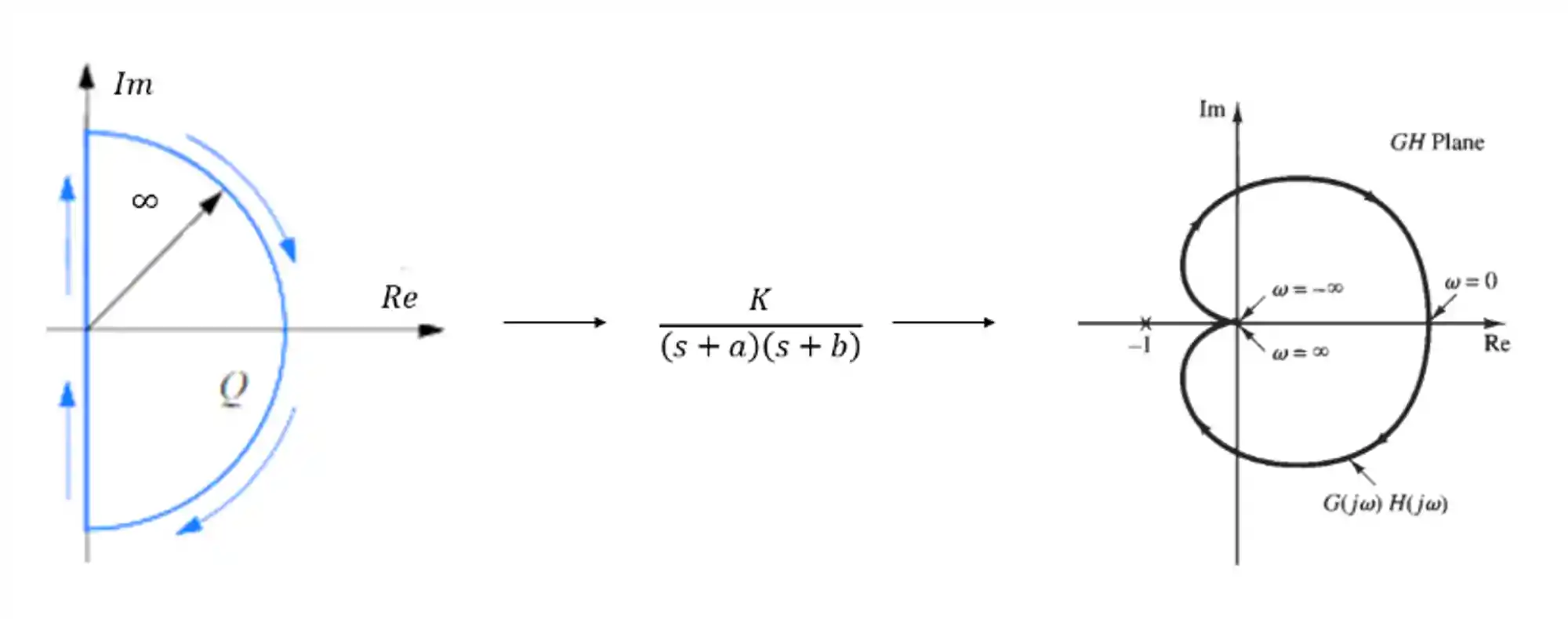
Diagrama de Nyquist: Mapeamento
Diagrama de Nyquist: Mapeamento

Para o exemplo acima, consideramos uma função em malha aberta com dois polos negativos. O contorno a ser mapeado é todo o semiplano positivo, dessa forma, o semicírculo da figura acima tem raio infinito, porque queremos mapear o semiplano inteiro. A função de mapeamento é a função de transferência em malha aberta e o contorno mapeado é o nosso diagrama de Nyquist.
Para fazer o mapeamento, devemos substituir por e variar a frequência () , de 0 a .


Vamos analisar isso melhor:

Para o exemplo acima, consideramos uma função em malha aberta com dois polos negativos. O contorno a ser mapeado é todo o semiplano positivo, dessa forma, o semicírculo da figura acima tem raio infinito, porque queremos mapear o semiplano inteiro. A função de mapeamento é a função de transferência em malha aberta e o contorno mapeado é o nosso diagrama de Nyquist.
Para fazer o mapeamento, devemos substituir s por iω e variar a frequência, , de 0 a .
Vamos analisar isso melhor:

Fazendo:

Sendo assim, para fazer o mapeamento, devemos ver como a função varia, quando variamos de a . Repare que quando a função se torna uma constante, quando é infinito, a função tende a . Além disso, como a função tem dois polos, nós vimos na aula de Diagrama de Bode que em altas frequências o ângulo de fase dessas funções é º, dessa forma, quando , a função tende a com um ângulo de º.

Uma outra característica dos Diagramas de Nyquist é que eles são simétricos em relação ao eixo dos reais. Então para obter o contorno completo, basta fazermos a frequência de até e depois obter o outro plano por simetria.

Como usar o Critério de Estabilidade de Nyquist

Como Usar

O critério de Nyquist nos permitir descobrir quantos zeros positivos da função existem. Como os zeros dessa função são os polos da função de transferência em malha fechada, nós automaticamente descobriremos quantos polos positivos em malha fechada existem. Lembrando que para um sistema ser estável, ele não pode possuir polos em malha fechada positivo. O critério de Nyquist é o seguinte:

Onde:

  • é o número de zeros positivos de ;
  • é o número de voltas que o diagrama de Nyquist dá em torno de ;
  • é o número de polos positivos da função de transferência em malha aberta.

Dessa forma, obtemos pelo diagrama de Nyquist, pela função de transferência em malha aberta e calculamos . Para o sistema ser estável em malha fechada, precisa ser . Vamos entender isso melhor com um exemplo.

Exemplo: Desenhe o Diagrama de Nyquist para a Função Abaixo

Sendo a e b positivos.

Para um K suficientemente grande, o diagrama de Nyquist será:

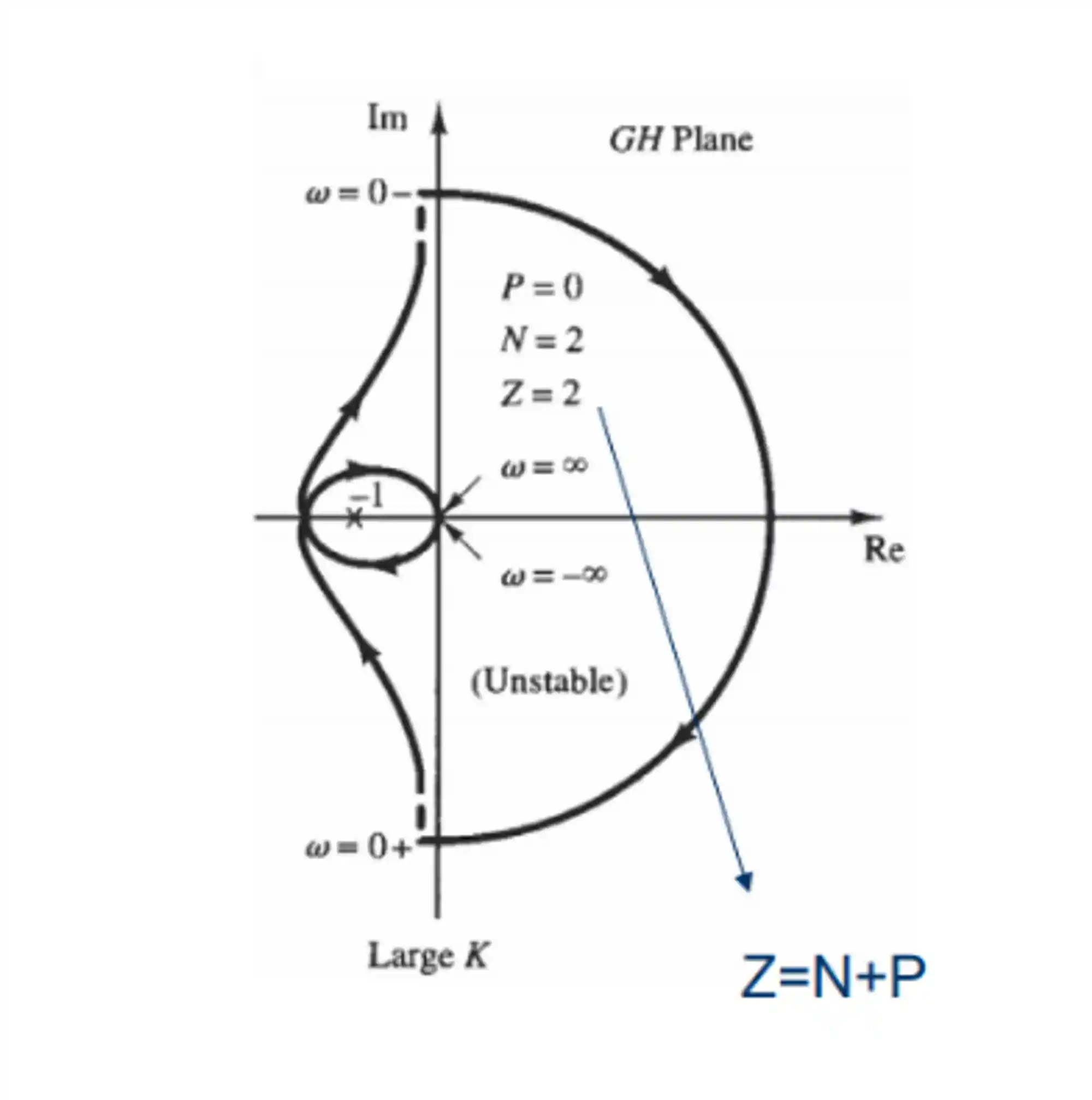
Diagrama de Nyquist
Diagrama de Nyquist

Para esse caso teremos , pois o digarama dá duas voltas em torno de
e , pois os dois polos da função de transferência em malha aberta são negativos.
Sendo assim:

Portanto, o sistema será instável em malha fechada! Lembrando que o número é positivo se a volta for no sentido horário e negativo se for no sentido anti-horário.

Como Fazer o Diagrama de Nyquist: Mapeamento de Contorno

Como usar o Critério de Estabilidade de Nyquist

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração própria

Use o critério de Nyquist para determinar a estabilidade de um sistema com realimentação unitária e função de transferência mostrada abaixo:

G s = 1 s + 1

Passo 1

Primeriamente precisamos fazer o esboço do diagrama de Nyquist para a função de transferência. Para isso, substituímos s por i ω e varíamos ω de 0 ate´ ∞ .

Substituindo s por i ω :

G i ω = 1 i ω + 1

Passo 2

Devemos agora esboçar o diagrama de Nyquist variando o valor de ω de 0 até ∞ . Usando um software conseguimos a seguinte imagem:

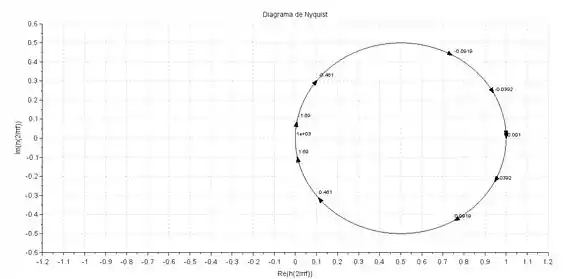
Os números ao longo da curva são referentes à frequência em que a função de transferência está sendo mapeada.

Repare que em ω = 0 o diagrama tende a 1 , e quando ω tende a ∞ o diagrama tende a zero, uma vez que o denominador será muito maior que o denominador da função de transferência.

Além disso, o diagram chega em 0 , formando um ângulo de 90 º . Isso acontece porque temos um polo a mais que zero nessa função de transferência.

Passo 3

Para determinar se o sistema é estável ou não, devemos determinar o número de raízes da equação característica em malha fechada no semiplano direito através da fórmula abaixo:

Z = N + P

Onde, Z é o número de raízes positivas da equação características, N é o número de voltas que o diagrama dá em - 1 , e P é o número de polos positivos em malha aberta. Para que o sistema seja estável não pode haver rízes positivas da equação característica, ou seja, Z = 0 .

Para este exemplo, N = 0 porque o diagrama não circula - 1 , e o único polo que existe em malha aberta é - 1 , logo, P = 0 .

Sendo asism:

Z = 0 + 0 = 0

O sistema é estável.

Resposta

Sistema estável

Exercício Resolvido #2

Elaboração própria

Use o critério de Nyquist para determinar a estabilidade de um sistema com realimentação unitária e função de transferência mostrada abaixo:

G s = s - 6 s + 1

Passo 1

Primeriamente precisamos fazer o esboço do diagrama de Nyquist para a função de transferência. Para isso, substituímos s por i ω e varíamos ω de 0 ate´ ∞ .

Substituindo s por i ω :

G i ω = i ω - 6 i ω + 1

Passo 2

Devemos agora esboçar o diagrama de Nyquist variando o valor de ω de 0 até ∞ . Usando um software, obtemos o seguinte Diagarama de Nyquist para a função:

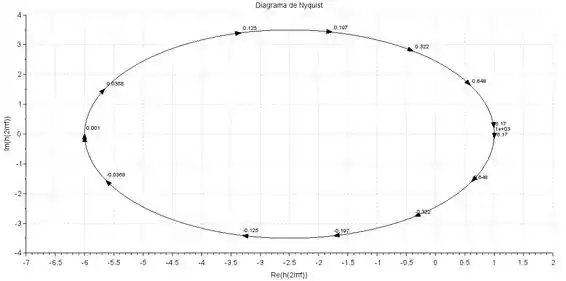
Em ω = 0 o diagrama tende a - 6 e quando ω assume valores muito altos o diagarama de Nyquist vai para 1 .

Passo 3

Para determinar se o sistema é estável ou não, devemos determinar o número de raízes da equação característica em malha fechada no semiplano direito através da fórmula abaixo:

Z = N + P

Onde, Z é o número de raízes positivas da equação características, N é o número de voltas que o diagrama dá em - 1 , e P é o número de polos positivos em malha aberta. Para que o sistema seja estável não pode haver rízes positivas da equação característica, ou seja, Z = 0 .

Para este exemplo, N = 1 porque o diagrama dá uma volta em - 1 no sentido ihorário, e o único polo que existe em malha aberta é - 1 , logo, P = 0 .

Sendo asism:

Z = 1 + 0 = 1

O sistema é instável.

Resposta

Sistema instável

Exercício Resolvido #3

Elaboração própria

Use o critério de Nyquist para determinar a estabilidade de um sistema com realimentação unitária e função de transferência mostrada abaixo:

G s = 40 ( s - 2 ) ( s + 10 )

Passo 1

Primeriamente precisamos fazer o esboço do diagrama de Nyquist para a função de transferência. Para isso, substituímos s por i ω e varíamos ω de 0 ate´ ∞ .

Substituindo s por i ω :

G i ω = 40 ( i ω - 2 ) ( i ω + 10 )

G i ω = 40 - ω 2 + 8 i ω - 20

Passo 2

Devemos agora esboçar o diagrama de Nyquist variando o valor de ω de 0 até ∞ . Usando um software, o diagrama de Nyquist é dado na figura abaixo:

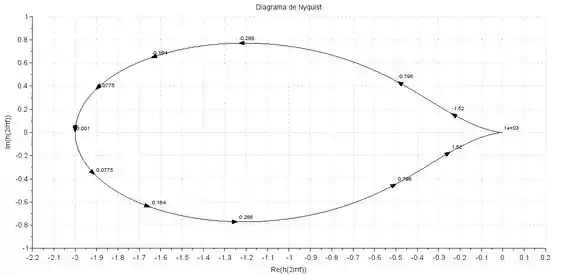
Em ω = 0 o diagrama tende a - 40 20 = - 2 , e quando ω assume valores muito altos o diagarama de Nyquist vai para 0 .

Além disso, podemos perceber em frequências altas, o ângulo de fase é - 180 º , já que existem dois polos a mais que zeros.

Passo 3

Para determinar se o sistema é estável ou não, devemos determinar o número de raízes da equação característica em malha fechada no semiplano direito através da fórmula abaixo:

Z = N + P

Onde, Z é o número de raízes positivas da equação características, N é o número de voltas que o diagrama dá em - 1 , e P é o número de polos positivos em malha aberta. Para que o sistema seja estável não pode haver rízes positivas da equação característica, ou seja, Z = 0 .

Para este exemplo, N = - 1 porque o diagrama dá uma volta em - 1 no sentido antihorário, e existe um polo positivo em malha aberta, 2 , logo, P = 1 .

Sendo asism:

Z = - 1 + 1 = 0

O sistema é estável.

Resposta

Sistema estável

Exercício Resolvido #4

Elaboração própria

Use o critério de Nyquist para determinar a estabilidade de um sistema com realimentação unitária e função de transferência mostrada abaixo:

G s = 30 ( s + 2 ) ( s + 10 )

Passo 1

Primeriamente precisamos fazer o esboço do diagrama de Nyquist para a função de transferência. Para isso, substituímos s por i ω e varíamos ω de 0 ate´ ∞ .

Substituindo s por i ω :

G i ω = 30 ( i ω + 2 ) ( i ω + 10 )

G i ω = 30 - ω 2 + 12 i ω + 20

Passo 2

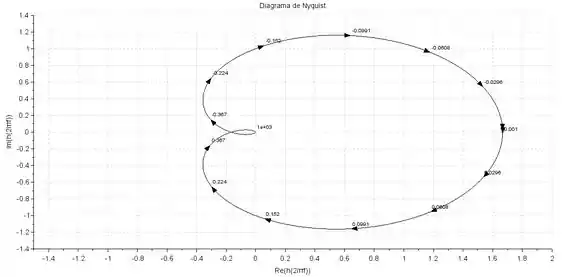
Devemos agora esboçar o diagrama de Nyquist variando o valor de ω de 0 até ∞ . Sendo assim, o diagrama de Nyquist ficará conforme mostra a figura abaixo:

Em ω = 0 o diagrama tende a 40 20 = 1,5 , e quando ω assume valores muito altos o diagarama de Nyquist vai para 0 .

Além disso, podemos perceber em frequências altas, o ângulo de fase é - 180 º , já que existem dois polos a mais que zeros.

Passo 3

Para determinar se o sistema é estável ou não, devemos determinar o número de raízes da equação característica em malha fechada no semiplano direito através da fórmula abaixo:

Z = N + P

Onde, Z é o número de raízes positivas da equação características, N é o número de voltas que o diagrama dá em - 1 , e P é o número de polos positivos em malha aberta. Para que o sistema seja estável não pode haver rízes positivas da equação característica, ou seja, Z = 0 .

Para este exemplo, N = 0 porque o diagrama não dá nenhuma volta em - 1 . Além disso, P = 0 , uma vez que não temos nenhum polo positivo em malha aberta.

Sendo asism:

Z = 0 + 0 = 0

O sistema é estável.

Resposta

Sistema estável

Exercício Resolvido #5

Elaboração própria

Use o critério de Nyquist para determinar a estabilidade de um sistema com realimentação unitária e função de transferência mostrada abaixo:

G s = 10 ( s + 1 ) ( s + 2 ) ( s + 3 )

Passo 1

Primeriamente precisamos fazer o esboço do diagrama de Nyquist para a função de transferência. Para isso, substituímos s por i ω e varíamos ω de 0 ate´ ∞ .

Substituindo s por i ω :

G i ω = 10 ( i ω + 1 ) ( i ω + 2 ) ( i ω + 3 )

Se efetuarmos as multiplicações teremos:

G i ω = 10 - i ω 3 - 6 ω 2 + 11 i ω + 6

Passo 2

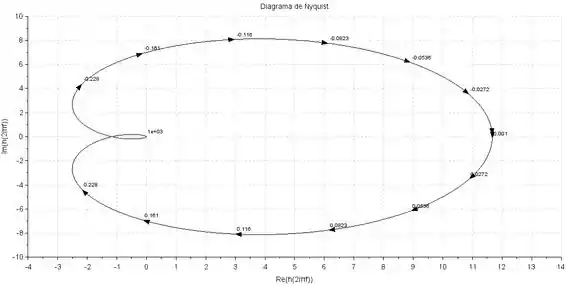
Devemos agora esboçar o diagrama de Nyquist variando o valor de ω de 0 até ∞ . Usado um software, o diagrama de Nyquist obtido é mostrado abaixo:

Em ω = 0 o diagrama tende a 10 6 = 1,67 , e quando ω assume valores muito altos o diagarama de Nyquist vai para 0 .

Além disso, podemos perceber em frequências altas, o ângulo de fase é - 270 º , já que existem três polos a mais que zeros, por isso, o diagrama precisa cruzar o eixo dos reais antes de “morrer” na origem.

Para calcular onde o diagrama cruza o eixo dos reais, precisamos encontrar as frequências que fazem com que a função de transferência seja um número real puro, ou seja:

- i ω 3 + 11 i ω = 0

Os valores de ω que satisfazem a expressão são ω = 0 que é de onde sai o diagrama e ω = 3,32 . Quando ω assume esse valor, teremos:

G 3,23 i = - 0,17

Passo 3

Para determinar se o sistema é estável ou não, devemos determinar o número de raízes da equação característica em malha fechada no semiplano direito através da fórmula abaixo:

Z = N + P

Onde, Z é o número de raízes positivas da equação características, N é o número de voltas que o diagrama dá em - 1 , e P é o número de polos positivos em malha aberta. Para que o sistema seja estável não pode haver rízes positivas da equação característica, ou seja, Z = 0 .

Para este exemplo, N = 0 porque o diagrama não dá nenhuma volta em - 1 . Além disso, P = 0 , uma vez que não temos nenhum polo positivo em malha aberta.

Sendo asism:

Z = 0 + 0 = 0

O sistema é estável.

Resposta

Sistema estável

Exercício Resolvido #6

Elaboração própria

Use o critério de Nyquist para determinar a estabilidade de um sistema com realimentação unitária e função de transferência mostrada abaixo:

G s = 70 ( s + 1 ) ( s + 2 ) ( s + 3 )

Passo 1

Primeriamente precisamos fazer o esboço do diagrama de Nyquist para a função de transferência. Para isso, substituímos s por i ω e varíamos ω de 0 ate´ ∞ .

Substituindo s por i ω :

G i ω = 70 ( i ω + 1 ) ( i ω + 2 ) ( i ω + 3 )

Se efetuarmos as multiplicações teremos:

G i ω = 70 - i ω 3 - 6 ω 2 + 11 i ω + 6

Passo 2

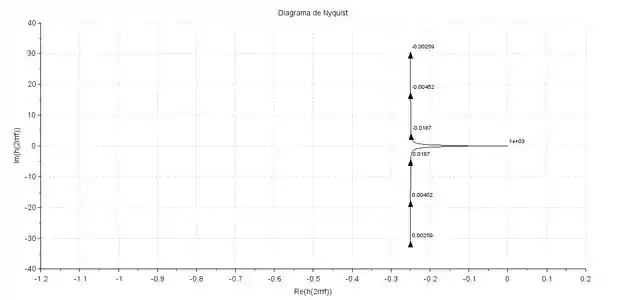
Devemos agora esboçar o diagrama de Nyquist variando o valor de ω de 0 até ∞ . Usando um software, conseguimos o seguinte diagrama de Nyquist para a função de transferência:

Em ω = 0 o diagrama tende a 70 6 = 11,67 , e quando ω assume valores muito altos o diagarama de Nyquist vai para 0 .

Além disso, podemos perceber em frequências altas, o ângulo de fase é - 270 º , já que existem três polos a mais que zeros, por isso, o diagrama precisa cruzar o eixo dos reais antes de “morrer” na origem.

Para calcular onde o diagrama cruza o eixo dos reais, precisamos encontrar as frequências que fazem com que a função de transferência seja um número real puro, ou seja:

- i ω 3 + 11 i ω = 0

Os valores de ω que satisfazem a expressão são ω = 0 que é de onde sai o diagrama e ω = 3,32 . Quando ω assume esse valor, teremos:

G 3,23 i = - 1,19

Passo 3

Para determinar se o sistema é estável ou não, devemos determinar o número de raízes da equação característica em malha fechada no semiplano direito através da fórmula abaixo:

Z = N + P

Onde, Z é o número de raízes positivas da equação características, N é o número de voltas que o diagrama dá em - 1 , e P é o número de polos positivos em malha aberta. Para que o sistema seja estável não pode haver rízes positivas da equação característica, ou seja, Z = 0 .

Para este exemplo, N = 2 porque o diagrama dá duas voltas em - 1 , ambas no sentido horário. Além disso, P = 0 , uma vez que não temos nenhum polo positivo em malha aberta.

Sendo asism:

Z = 2 + 0 = 2

O sistema é instável.

Resposta

Sistema instável

Exercício Resolvido #7

Elaboração própria

Use o critério de Nyquist para determinar a estabilidade de um sistema com realimentação unitária e função de transferência mostrada abaixo:

G s = 1 s ( s + 2 )

Passo 1

Primeriamente precisamos fazer o esboço do diagrama de Nyquist para a função de transferência. Para isso, substituímos s por i ω e varíamos ω de 0 ate´ ∞ .

Substituindo s por i ω :

G i ω = 1 i ω ( i ω + 2 )

Se efetuarmos as multiplicações teremos:

G i ω = 70 - ω 2 + 2 i ω

Passo 2

Devemos agora esboçar o diagrama de Nyquist variando o valor de ω de 0 até ∞ . Fazendo uso de um software, obtivemos:

Em ω = 0 o diagrama tenderá a infinito, e quando ω tede a infinito, o diagrama tende à origem.

Além disso, podemos perceber em frequências altas, o ângulo de fase é - 180 º , já que existem dois polos a mais que zeros, isso quer dizer que o diagrama se aproximará da origem formando um ângulo de - 180 º .

Passo 3

Para determinar se o sistema é estável ou não, devemos determinar o número de raízes da equação característica em malha fechada no semiplano direito através da fórmula abaixo:

Z = N + P

Onde, Z é o número de raízes positivas da equação características, N é o número de voltas que o diagrama dá em - 1 , e P é o número de polos positivos em malha aberta. Para que o sistema seja estável não pode haver rízes positivas da equação característica, ou seja, Z = 0 .

Para este exemplo, N = 0 já que o diagrama não dá nenhuma volta em - 1 . Além disso, P = 0 , uma vez que não temos nenhum polo positivo em malha aberta.

Sendo asism:

Z = 0 + 0 = 0

O sistema é estável.

Resposta

Sistema estável

Exercício Resolvido #8

Elaboração própria

Use o critério de Nyquist para determinar a estabilidade de um sistema com realimentação unitária e função de transferência mostrada abaixo:

G s = 100 s ( s + 3 ) ( s + 6 )

Passo 1

Primeriamente precisamos fazer o esboço do diagrama de Nyquist para a função de transferência. Para isso, substituímos s por i ω e varíamos ω de 0 ate´ ∞ .

Substituindo s por i ω :

G i ω = 100 i ω ( i ω + 3 ) ( i ω + 6 )

Se efetuarmos as multiplicações teremos:

G i ω = 70 - i ω 3 - 9 ω 2 + 18 i ω

Passo 2

Devemos agora esboçar o diagrama de Nyquist variando o valor de ω de 0 até ∞ . Sendo assim, o diagrama de Nyquist ficará conforme mostra a figura abaixo:

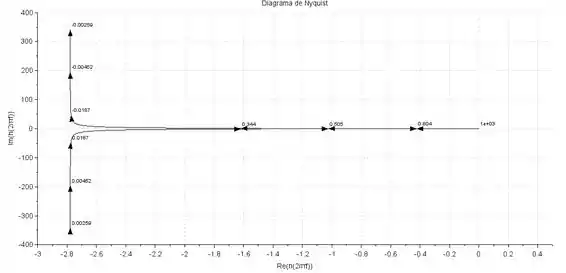
Em ω = 0 o diagrama tenderá a ∞   , e quando ω assume valores muito altos o diagarama de Nyquist vai para 0 .

Além disso, podemos perceber em frequências altas, o ângulo de fase é - 270 º , já que existem três polos a mais que zeros, por isso, o diagrama precisa cruzar o eixo dos reais antes de “morrer” na origem com o ângulo adequado, formando um loop. Como esse loop é muito pequeno, precisamos dar um zoom no diagrama para conseguir enxergar bem:

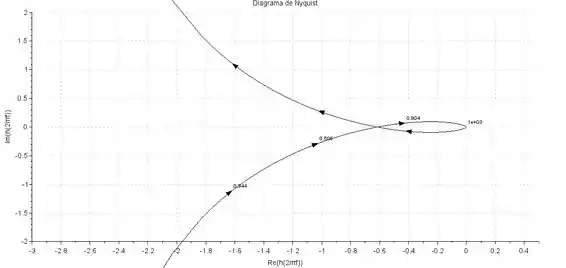
Para calcular onde o diagrama cruza o eixo dos reais, precisamos encontrar as frequências que fazem com que a função de transferência seja um número real puro, ou seja:

- i ω 3 + 18 i ω = 0

Os valores de ω que satisfazem a expressão são ω = 0 que é de onde sai o diagrama (no infinito) e ω = 4,24 . Quando ω assume esse valor, teremos:

G 4,24 i = - 0,6

Passo 3

Para determinar se o sistema é estável ou não, devemos determinar o número de raízes da equação característica em malha fechada no semiplano direito através da fórmula abaixo:

Z = N + P

Onde, Z é o número de raízes positivas da equação características, N é o número de voltas que o diagrama dá em - 1 , e P é o número de polos positivos em malha aberta. Para que o sistema seja estável não pode haver rízes positivas da equação característica, ou seja, Z = 0 .

Para este exemplo, N = 0 porque o diagrama não dá nenhuma volta em - 1 . Além disso, P = 0 , uma vez que não temos nenhum polo positivo em malha aberta.

Sendo asism:

Z = 0 + 0 = 0

O sistema é estável.

Resposta

Sistema estável