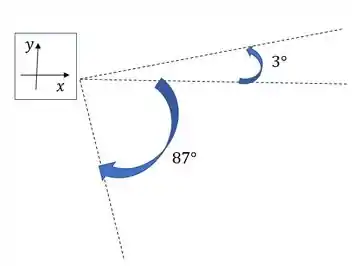
O elemento mostrado na figura está rotacionado de 30° no sentido horário. Sabendo disso determine o valor das tensões principais e suas respectivas orientações.
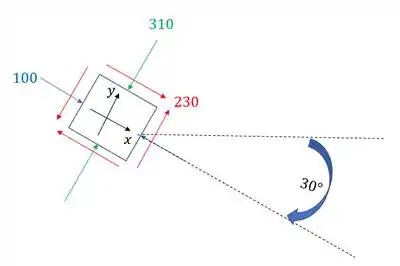
Passo 1
Sabemos pela teoria quais fórmulas nos auxiliam nisso, sendo essas fórmulas dadas por
Que nos fornece o plano em que as tensões principais ocorrem
Que nos fornece a média das tensões
Que nos da o cisalhante máximo que o nosso elemento foi submetido
A ultima fórmula é dada por
Que de fato nos fornece o valor das tensões principais
Passo 2
Assim como temos as fórmulas, também temos os dados necessários para resolver a questão, que são dados por
Vamos resolvendo agora cada fórmula passo a passo
Primeiro vamos determinar a orientação em que ocorre as tensões principais
Isso é uma das orientações dos planos, mas também pode-se encontrar o outro subtraindo 90° do que encontramos
Passo 3
Agora que já sabemos qual é a orientação do plano, vamos determinar os valores necessários para encontrarmos os valores das tensões principais.
Sabemos que
Então
Também sabemos que
Logo
Passo 4
Como já temos esses valores, podemos facilmente determinar os valores das tensões máximas pelas fórmulas
Substituindo
O cisalhante máximo é muito simples, é o próprio valor do R que já calculamos
Passo 5
Agora devemos descobrir qual a orientação de cada plano. Com relação as tensões principais sabemos que
E sabemos que
Agora precisamos usar a fórmula
Substituiremos os nossos valores dado no elemento e escolheremos um dos ângulos para testar, assim saberemos a qual tensão cada ângulo pertence
Fazendo
Teremos que
então
E
Se já descobrimos a quem pertence um dos ângulos, com certeza o outro pertence a outa tensão.
Desenhando esse elemento teremos que
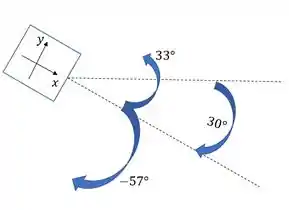
Logo