Teoria
Só falta essa!! Vamos lá, galera!

Hipérbole
A hipérbole parece duas parábolas simétricas, como mostra a figura a seguir:
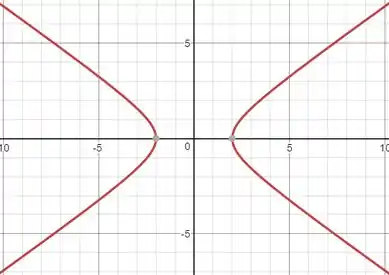
A definição da hipérbole talvez seja a mais cheia de “mimimi”!! Mas, vamos te explicar direitinho!!
Se considerarmos no plano dois pontos distintos e tal que a distância , . Seja um número real tal que .
Então, hipérbole é o nome do conjunto de pontos do plano tal que:
Agora que conhecemos a definição, vamos ver os principais elementos da hipérbole!!
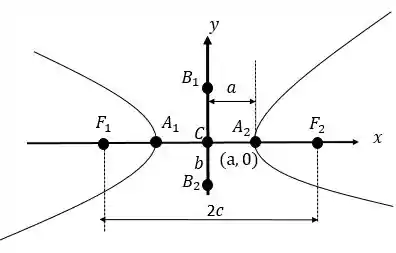
- Focos: pontos e
- Distância Focal: é a distância entre os focos
- Centro: Ponto , ponto médio do segmento
- Vértices: pontos e
- Eixo real ou transverso: é o segmento de comprimento
- Eixo imaginário ou conjugado: é o segmento de comprimento
- Caso 1: O eixo real está sobre o eixo dos
- Caso 2: O eixo real está sobre o eixo dos
- Caso 3: Translação
O valor de pode ser obtido por meio da seguinte relação:
CUIDADO para não confundir essa relação com a da elipse!!
A excentricidade da hipérbole é calculada da mesma forma que a da elipse, , porém agora na hipérbole , pois .
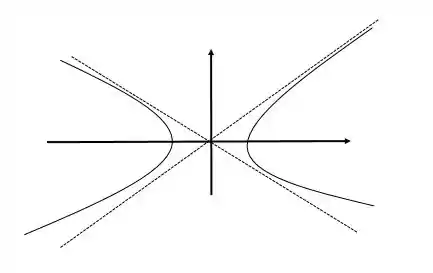
O último elemento importante são as assíntotas, que na figura acima são as retas tracejadas.
Vamos colocar tudo o que vimos de forma prática, dividindo em 3 casos:
Caso 1:
Considerando um ponto um ponto qualquer de uma hipérbole de focos e .
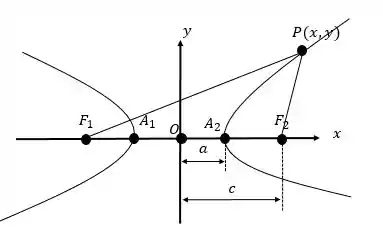
Usando a definição:
Fazendo as contas, chega-se em:
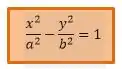
Essa é a equação reduzida ou canônica da hipérbole de centro na origem e eixo real sobre o eixo . Para esse caso nossos elementos são:
Assíntotas:
Caso 2:
Fazendo o mesmo procedimento do anterior, mas agora considerando a figura a seguir, temos:
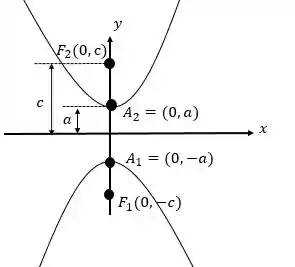
A expressão fica:
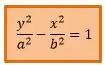
Essa é a equação reduzida ou canônica da hipérbole de centro na origem e eixo real sobre o eixo .
Para esse caso nossos elementos são:
Assíntotas:
Caso 3:
No caso da translação temos duas possibilidades mostradas na figura a seguir:
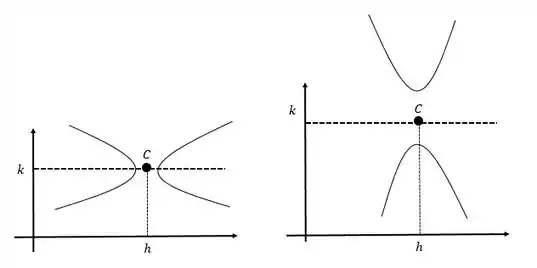
Uma translação nada mais é que deslocarmos o centro da hipérbole, ou seja, nos casos 1 e 2 os centros eram , agora, os centros estão deslocados. Então, nossos centros serão:
Nossas equações ficarão:
Então, para resolver usaremos o mesmo esquema que para a parábola:
- Escrever em um sistema de coordenadas , que possui relações
- Achar todos os elementos no sistema considerando um dos casos 1 ou 2.
- Passar do sistema para o nosso tradicional
Note que:
- O valor de está sempre associado à parcela positiva, ou seja, ou
Pronto!! Agora sim, terminamos a teoria!!

Bora praticar, então?!!