Superfícies
Teoria
Você já imaginou se pegássemos uma curva, por exemplo, uma parábola e nela colocássemos um conjunto de retas paralelas, qual superfície obteríamos??
Não sabe ou nem consegue imaginar?? E se eu te dissesse que você já conhece vários tipos de superfícies? Por exemplo, rolos de papel higiênico é um exemplo perfeito para as superfícies cilíndricas, um chapéu de festa de aniversário é uma superfície cônica e aqueles corpos curvilíneos são um exemplo de superfícies de revolução!
Ok, mas o que são de fato as superfícies cilíndricas, cônicas e de revolução? Como representar essas superfícies algebricamente?
Relaxa Aí!! Vamos te ensinar direitinho como são formadas as superfícies cilíndricas, cônicas e de revolução ;).
Superfícies Cilíndricas
Para a gente forma a superfície cilíndrica, precisamos primeiro de uma diretriz, ou seja, uma curva que vamos usar de base para a superfície cilíndrica.
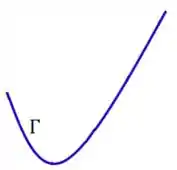
Para criar a superfície de fato, precisamos de um conjunto de retas paralelas a uma reta , chamadas de geratriz, que contém algum ponto da curva :
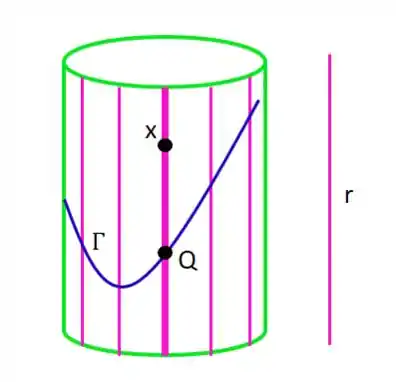
Se você der uma olhada na figura acima, repara que todas as retas paralelas à (em rosa) tem um ponto em comum com a reta diretriz (em azul) e é isso que vai definir a nossa superfície cilíndrica!
Ainda tá um pouco confuso??
Vamos te ensinar o passo a passo de como obter a equação da superfície!!
Considerando a diretriz e geratrizes paralelas a , sendo um vetor diretor de e
Pela definição, temos que um ponto pertence à superfície se, e somente se, existem um ponto de e um número real tal que . Podemos então escrever que:
Para garantir que pertence à superfície, então existe um número real tal que
Pronto!! Com as duas relações acima conseguimos encontrar a equação da superfície cilíndrica!!
Vamos ver um exemplo para ficar mais claro!
Exemplo:
Vamos achar a equação da superfície cilíndrica de diretriz e reta .
Beleza, a primeira coisa que faremos é igual a sua equação original
Vai ficar assim, ô
Da equação de , temos que . Substituindo isso em
Temos que,
Agora, vamos substituir em para achar a bendita equação da superfície cilíndrica!
De tiramos que . Substituindo isso em e simplificando, obtemos:
Que é a equação da superfície cilíndrica!!!! UHULLLLL
Viu só?? Os exercícios são bem mais simples do que a teoria!
Superfícies Cônicas
Para gerar uma superfície cônica vamos precisar novamente de uma diretriz, mas além disso também vamos precisar de um Vértice :
A superfície cônica vai ser definida pelo conjunto de retas, chamadas de geratriz, que contém o vértice e algum ponto de , chamada de. Reparem que NÃO contém o vértice!
Como fizemos anteriormente, vamos explicar como obter as equações da superfície!!
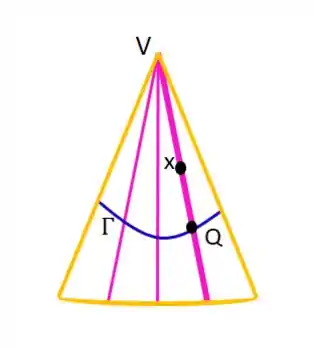
Considerando uma superfície cônica de diretriz e vértice sendo e
Pela definição, um ponto , distinto de , pertence à superfície se, e somente se, existe um ponto em e tais que . Escrevendo com equações paramétricas, temos
Assim, pertence à superfície se, e somente se, ou existe um número real tal que
Com as duas equações acima conseguimos determinar a equação da superfície cônica!! ;)
Vamos ver um exemplo!
Exemplo:
Ache a equação da superfície cônica com e diretriz .
Vamos resolver igualzinho o da superfície cilíndrica!
Então, vamos escrever a equação da diretriz que nem a sua forma original,
Como o vértice é , vamos substituir em
E ficaremos com:
Substituindo em , temos
De tiramos que . Substituindo essa relação em e simplificando, obtemos:
E essa é a equação da nossa superfície cônica!!!! YEYYYY
Estamos quase terminando a teoria!! Para finalizar vamos falar sobre superfície de revolução!!
Superfícies de Revolução
As superfícies de revolução estão muito presentes no nosso dia a dia e nós as vemos sempre!
Um exemplo de superfície de revolução diferente do já citado no inicio é a superfície esférica, que pode ser formada rotacionando uma semi circunferência (arco de ) em torno de um eixo.
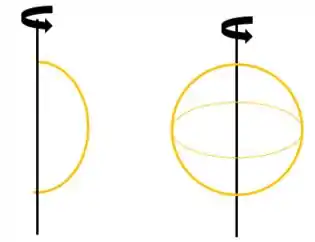
Agora vamos definir o que são essas superfícies! Olhando na figura abaixo, a superfície de revolução é definida pelo conjunto de circunferências, cujos centros pertencem à e interceptam . Ou seja, é a superfície formada pela rotação de uma curva () em torno de .
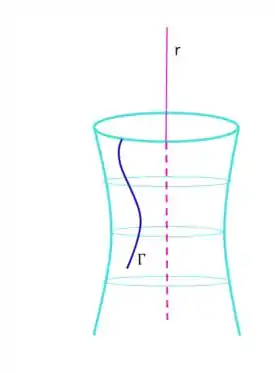
Reparem que as circunferências estão em planos perpendiculares à , como o plano em verde, mostrado no segundo desenho.
Nessa superfície se chama geratriz e agora será o eixo de rotação ou eixo de simetria.
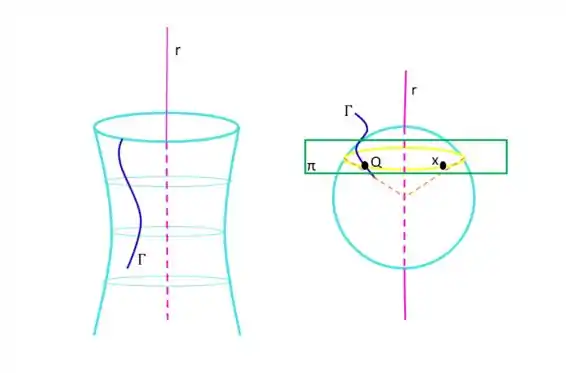
Assim, para obter as equações da superfície gerada pela rotação de em torno de vamos considerar que:
- Considerando um ponto pertencente a .
- o vetor diretor de
E que
Para encontrar a equação da superfície devemos satisfazer todas as regras da definição:
1- Um ponto pertence à superfície se, e somente se, pertence a um paralelo que intercepta em .
2- O paralelo é a interseção do plano que contém e é perpendicular a , , com a superfície esférica de centro que contém , ou seja, . Logo, pertence a superfície se, e somente se, existem números reais e tais que e
Com as quatro relações acima devemos encontrar uma relação entre de forma que conseguimos escrever a equação da superfície apenas em função de e .
Vamos fazer um exemplinho!
Exemplo:
Vamos achar a equação da superfície de revolução com , eixo de simetria e centro .
A resolução desse exercício é um pouco diferente dos outros que fizemos, mas também é bem tranquila! Olha só:
Vamos escrever na sua forma original
Sabemos que e . Com isso escrevemos a relação
Que fica:
Assim, formamos o sistema:
Resolvendo em função de , temos a resposta
Terminamos a teoria!! Ufa!
Não deixe de fazer os exercícios para entender bem essa teoria chatinha!!
Bora praticar?!
Superfícies Cônicas
Superfícies de Revolução
Exercícios Resolvidos
Exercício Resolvido #1
Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 315-1.
Ache uma equação da superfície cilíndrica de diretriz
Cujas geratrizes são paralelas à reta
Passo 1
Chegou a hora de praticarmos Superfícies Cilíndricas!! Vamos colocar em prática o que vimos na teoria ;).
Passo 2
Começaremos identificando o que o problema nos fornece de dados!!
Primeiro, temos as duas equações da diretriz da superfície que são:
Na teoria essas duas expressões foram escritas da seguinte forma:
No nosso exercício o e o são:
A outra informação que temos é que as retas geratrizes são paralelas à reta com equações paramétricas:
Fazendo o comparativo com a teoria, essa reta é a reta .
Então, por meio dessas equações paramétricas que iremos tirar o vetor diretor de !
Lembra como faz isso?? NÃO? =O
Calma lá, vamos te mostrar!
Quando temos equações paramétricas de uma reta:
onde o nosso parâmetro é o c, então as coordenadas de um ponto que pertence a essa reta são dadas por e o vetor diretor da reta é o vetor de coordenadas
Se você quiser uma explicação mais detalhada, dá uma olhadinha lá no tópico de Introdução às Retas, beleza?? =)
Mas nesse caso aí, chegamos ao vetor diretor:
Passo 3
Sabendo o vetor diretor de , conseguimos montar a relação:
Substituindo temos:
Passo 4
Estamos quase terminando!!
Do sistema que encontramos anteriormente,
Na segunda equação vamos isolar , teremos que:
Vamos então, substituir essa relação na primeira equação:
Pronto!! Chegamos na equação da superfície cilíndrica!!
Resposta
Exercício Resolvido #2
Unicamp, 2ª Chamada – Geometria Analítica, 20/06/2013 (manhã), pág. 1, Questão 3
Encontrar a equação (em coordenadas cartesianas) da superfície cilíndrica com curva diretriz a cônica no plano e retas geratrizes paralelas ao vetor .
Passo 1
Para ficarmos afiados em superfícies cilíndricas vamos resolver mais um exercício parecido com o anterior!!
O enunciado nos dá três informação:
- Curva diretriz a cônica
- Sendo que está no plano , ou seja, .
- Retas geratrizes paralelas ao vetor
Passo 2
Vamos começar a montar nossas expressões. A curva diretriz da nossa superfície será:
Como temos que . Podemos escrever que:
Susbtituindo no sistema teremos então:
Isolando :
Substituindo:
Pronto!! Mais uma vez chegamos na expressão da nossa superfície cilíndrica!!
Resposta
Exercício Resolvido #3
Unicamp, Lista 3 – Geometria Analítica, 2014, pág. 1, Ex. 6. Modificado
Mostre que cada uma das equações representa uma superfície cilíndrica e determine a equação da curva diretriz e um vetor paralelo às retas geratrizes.
Passo 1
Temos agora o problema inverso do que fizemos anteriormente. Agora, já temos a equação da nossa superfície e queremos descobrir a equação da curva diretriz e um vetor paralelo às retas geratrizes.
Passo 2
a)
Nesse tipo de problema, primeiro, precisamos escrever nossa equação no formato:
Reescrevendo, temos:
Fazendo o caminho inverso temos que:
Então:
Ficamos com a expressão:
Podemos então igualar:
Das equação e acima, tiramos que:
Portanto:
Então, nosso vetor diretor das retas geratrizes são:
E a expressão é a curva:
Passo 3
Depois de todas essas manipulações, chegamos que:
Como importa apenas a direção da reta , podemos dizer que:
Resposta
Exercício Resolvido #4
Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 321-2.
Ache uma equação da superfície cônica de vértice que tem por diretriz a circunferência
Passo 1
Chegou a hora de ficarmos craques em superfícies cônicas!! Hehe
Para isso o exercício pede para determinarmos a equação da superfície cônica que possui:
- Vértice -
- Diretriz a circunferência
Passo 2
Da teoria vimos que se definirmos nosso vértice como sendo e definirmos nossa diretriz como:
A equação da nossa superfície será o sistema:
Passo 3
Já demos uma revisada rápida na teoria. Agora, vamos colocar em prática:
Susbituindo as mudanças de variáveis de em , temos:
Isolando da expressão :
Substituindoa relação na expressão a seguir:
Reescrevendo a expressão acima:
Ufa!! Acabou!!
Resposta
Exercício Resolvido #5
Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 322-1.
Ache uma equação da superfície cônica de vértice cuja diretriz é a parábola
Passo 1
Vamos lá para mais um exercício de superfície cônica!! Hehe
Novamente, o enunciado nos dá o vértice e a diretriz que é a parábola definida pelas equações .
Passo 2
Da teoria sendo e definirmos nossa diretriz como:
A equação da nossa superfície será o sistema:
Passo 3
Substituindo, temos:
Susbituindo as mudanças de variáveis de em , temos:
Isolando da expressão :
Substituindoa relação na expressão a seguir:
Reescrevendo a expressão acima:
Acabamos!! Já estamos craques!! Haha
Resposta
Exercício Resolvido #6
Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 325-1.
Ache uma equação da superfície de rotação gerada pela curva
Em torno da reta
Passo 1
Chegou a hora das superfícies de rotação!!
O enunciado nos dá a curva que será rotacionada em torno da reta .
Passo 2
Na teoria vimos que para resolver esse tipo de problema temos que ter três informações:
- um ponto pertencente a .
- o vetor diretor de
E
Do nosso enunciado conseguimos tirar que:
Passo 3
Na teoria temos que:
Escrevendo com os valores que temos:
Assim, temos equações:
Susbtituindo em , temos:
Substituindo em :
Da expressão temos que , substituindo na expressão essa relação e que teremos o seguinte sistema:
Devemos achar uma relação entre e tal que , para isso vamos subtrair e :
Coma relação e as expressões e podemos escrever a equação da nossa superfície de revolução:
Uhulllll!! Terminamos!! ;)
Resposta
Exercício Resolvido #7
Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 328-5.
Obtenha uma equação da superfície gerada pela parábola
Quando gira em torno de .
Passo 1
Para finalizar nosso estudo sobre superfícies vamos fazer mais um exercício sobre superfícies de revolução!!!
Esse exercício é muito parecido com o anterior. O que muda é que não nos foi dado explicitamente o vetor diretor e um ponto pertencente à reta de revolução.
Passo 2
Primeiro, vamos pegar as informações sobre a reta de revolução. A reta é o eixo . Quando estudamos “Planos e Retas” vimos que a equação do eixo pode ser escrita da seguinte forma:
Assim, temos que:
Pronto, já temos as informações da reta que precisamos. Agora, é juntar todas as informações com a teoria!!
Passo 3
Para achar a equação da superfície devemos satisfazer as equações:
Susbtituindo com os valores e expressões do nosso problema temos:
Passo 4
Com as relações acima chegamos no seguinte sistema:
Susbtituindo a relação em e a relação em , temos o sistema:
Da relação , temos:
Susbituindo a relação acima em :
Rearranjando,
Susbtituindo as expressões e temos a expressão da superfície:
Ufaa!!Terminamos!!!
