Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Callioli - Álgebra Linear e Aplicações - Parte 2- Ed: 6º - Capítulo 1.1 - Ex. 2b

Achar os valores e os vetores próprios do operador linear T do R 2 dado por

b)   T 1 ,   0 ,   0 = ( 0 ,   0 ,   0 ) ,     T ( 0 ,   1 ,   0 ) = ( 0 ,   0 ,   0 )   e   T ( 0 ,   0 ,   1 )   =   ( 5 ,   - 1 ,   2 ) .  

Passo 1

Primeiro, vamos colocar em forma de matriz de T 1 ,   0 ,   0 = 0 ,   0 ,   0 ,     T 0 ,   1 ,   0 = 0 ,   0 ,   0 e   T 0 ,   0 ,   1 = ( 5 ,   - 1 ,   2 ) . Para isso vamos colocar em um sistema para ficar claro

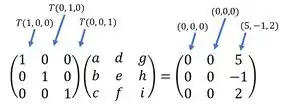
Você reparou que a primeira matriz é a identidade? Isso significa que qualquer matriz multiplicada pela identidade vai resultar a própria matriz, dessa forma

a d g b e h c f i = 0 0 5 0 0 - 1 0 0 2

Encontramos a matriz! Vamos usar a formulazinha para descobrir os valores próprios

det ⁡ ( A - I λ ) = 0

Lembrando que I é a matriz identidade e o λ é o valor que queremos descobrir, logo

I λ = λ 0 0 0 λ 0 0 0 λ

Passo 2

Vamos subtrair

0 0 5 0 0 - 1 0 0 2 - λ 0 0 0 λ 0 0 0 λ = - λ 0 5 0 - λ - 1 0 0 2 - λ

Certinho? Então descobrimos A - I λ , agora falta colocar no determinante!

- λ 0 5 0 - λ - 1 0 0 2 - λ - λ 0 0 - λ 0 0

Então calculando o determinante temos a equação característica

2 λ 2 - λ 3

Uhuul! Encontramos o polinômio característico! Resolvendo

λ 2 2 - λ = 0

Os autovalores são

λ 1 = 2 ,   λ 2 = 0 ,   λ 3 = 0

Bora encontrar os vetores próprios?

Passo 3

Começando para λ 1 = 2

- λ 0 5 0 - λ - 1 0 0 2 - λ = - 2 0 5 0 - 2 - 1 0 0 0

Colocando em um sisteminha teremos

- 2 0 5 0 - 2 - 1 0 0 0 x 1 x 2 x 3 = 0 0 0

A matriz estendida será

- 2 0 5 0 0 - 2 - 1 0 0 0 0 0

Fazendo Gauss-Jordan para simplificar a matriz, teremos

2 0 - 5 0 0 2 1 0 0 0 0 0

No sistema então

2 x 1 - 5 x 3 = 0     2   x 2 + x 3 = 0   x 3 = t   → x 1 = 5 2 x 3 x 2 = - 1 2 x 3 x 3 = t   → x 1 = 5 2 t x 2 = - 1 2 t x 3 = t  

Logo o vetor é

5 2 t ,   - 1 2 t ,   t → t 5 2 ,   - 1 2 ,   1 → 5 2 ,   - 1 2 ,   1

Passo 4

Para λ 2 = λ 3 = 0

- λ 0 5 0 - λ - 1 0 0 2 - λ = 0 0 5 0 0 - 1 0 0 2

Colocando em um sisteminha teremos

0 0 5 0 0 - 1 0 0 2 x 1 x 2 x 3 = 0 0 0

A matriz estendida será

0 0 5 0 0 0 - 1 0 0 0 2 0

Fazendo Gauss-Jordan para simplificar a matriz, teremos

0 0 1 0 0 0 0 0 0 0 0 0

No sistema,

x 1 = t x 2 = s x 3 = 0  

Assim os vetores são

t , s ,   0 → t 1 ,   0 ,   0 + s 0 ,   1 ,   0

Resposta

2, 5 2 ,   - 1 2 ,   1

0, (1, 0, 0) e (0, 1, 0)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sejam A e B matrizes triangulares com a mesma diagonal principal ( a i i=b j j ,i =1 ,. . . ,n ) . Prove que: P A ( t )=P B ( t )
Determinar valores próprios do operador linear T : V → V do R 4 que é definido em uma base { e 1 ,..., e n } por T e i = λ i ∈ R .
Seja A uma matriz triangular, ou seja, uma matriz A=( a i j ) tal que a i j = 0 sempre que ij (ou, ao contrário, a i j = 0 , sempre que i
Achar os valores e os vetores próprios do operador T do IR 2 dado por:T(x, y) = (-x, - y);
Achar os valores e os vetores próprios do operador T do R 2 dado por:c. T ( 1 ,0 )=( 0 ,- 1 )eT ( 0 ,1 )=( 1 ,0 )