Exercícios de Calculando Autovalores e Autovetores - Lista de Exercícios Resolvida
Questão 2
Calcular os autovalores e os correspondentes autovetores próprios das seguintes matrizes:
Ver solução completa
Questão 4
Seja um espaço vetorial de dimensão e um operador linear. Denote por o operador identidade de . Considere as seguintes afirmações.
- Se é autovalor de , então a dimensão da é menor ou igual à
- Tem pelo menos um autovalor
- Tem no máximo autovalores
Questão 5
Os autovalores da matriz
![]()
são:
(a) -1 e 3
(b) -1 e 4
(c) -2 e 2
(d) -2 e 3
Ver solução completaQuestão 6
Seja uma matriz . Assinale a alternativa FALSA:
pode não possuir autovetores
Se então os autovalores de podem ser e
pode ter apenas o autovalor e não ser a matriz identidade
Se então é autovalor
Ver solução completaQuestão 8
Seja uma matriz .
Assinale a afirmativa VERDADEIRA:
pode ter apenas um autovetor
sempre possui dois autovetores linearmente independentes
sempre possui dois autovetores
pode não ter autovetores
Ver solução completaQuestão 9
Considere
Marque a alternativa VERDADEIRA:
possui três autovalores distintos
é invertível
O núcleo de tem dimensão
O sistema não possui solução
Ver solução completaQuestão 10
Sabendo que os autovalores da transformação associada à matriz são e , então as dimensões de seus autoespaços, e , são respectivamente:
e
e
e
e
Ver solução completaQuestão 15
Seja
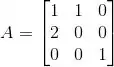
Os autovetores de A associado ao autovalor 2 são da forma:
(a)
(b)
(c)
(d)
Ver solução completaQuestão 16
A soma dos módulos dos autovalores da matriz é:
(a) 4
(b) 6
(c) 7
(d) 8
Ver solução completaQuestão 18
Assinale a soma dos módulos das componentes de um autovetor unitário associado ao menor autovalor da matriz:
Ver solução completa
Questão 19
Considere as seguintes afirmações:
Os autovalores de uma matriz são os mesmos da sua forma escalonada.
Se é autovalor de , uma matriz invertível, então é autovalor de com os mesmos autovetores de .
Qual das opções abaixo é CORRETA?
A afirmativa é falsa e é verdadeira.
A afirmativa é verdadeira e é verdadeira.
A afirmativa é verdadeira e é falsa.
A afirmativa é falsa e é falsa.
Ver solução completaQuestão 20
Considere as afirmativas abaixo:
Uma matriz , , sempre tem um autovetor.
Uma matriz sempre tem um autovetor
(a) é falsa e é verdadeira
(b) Ambas são falsas
(c) Ambas são verdadeiras
(d) é verdadeira e é falsa
Ver solução completaQuestão 21
Considere a matriz
Os autovetores de que não pertencem ao Núcleo de satisfazem:
(a) O dobro da primeira componente é igual ao triplo da segunda
(b) O triplo da primeira componente é igual a menos a segunda
(c) O dobro da primeira componente é igual a menos o triplo da segunda
(d)a primeira componente é a metade da segunda
Ver solução completaQuestão 22
Seja um autovetor da matriz associado ao maior dos autovalores de . Então vale:
Ver solução completa
Questão 24
Os autovalores da matriz são:
a) 4 e 8.
b) 3 e 6.
c) 4 e 6.
d) 3 e 7.
e) Não sei.
Ver solução completaQuestão 25
Seja uma matriz com polinômio característico . Considere as afirmações:
é falsa, mas é verdadeira.
e são falsas.
e são verdadeiras.
é verdadeira, mas é falsa.
Ver solução completaQuestão 26
Seja uma matriz tal que e . Assinale a única afirmativa INCORRETA:
a) Pode-se afirmar que
b) Pode-se afirmar que
c) Pode-se afirmar que
d) Pode-se afirmar que
e) Não sei.
Ver solução completaQuestão 31
Seja uma matriz quadrada. Assinale a alternativa VERDADEIRA:
Se os autovalores de são diferentes de zero, então é sobrejetiva.
Se os coeficientes de são diferentes de zero, então os autovalores de são diferentes de zero.
Se os coeficientes de são diferentes de zero, então é injetiva.
Se os autovalores de são diferentes de zero, então os coeficientes de são diferentes de zero.
Ver solução completaQuestão 35
Seja uma matriz quadrada. Considere as afirmativas abaixo:
- Se a soma dos elementos de cada linha de é igual a uma constante , então é um autovalor de .
- Se a soma dos elementos de cada coluna de é igual a uma constante , então é um autovalor de .
Ambas são falsas
é falsa e é verdadeira
Ambas são verdadeiras
é verdadeira e é falsa
Ver solução completaQuestão 36
Seja .
(b) Determine bases para os autoespaços correspondentes a cada autovalor.
Ver solução completaQuestão 38
A matriz é simétrica com autovalores , e . Sabemos que e são autovetores de .
(a) Determine os autoespaços de
Ver solução completaQuestão 39
A matriz possui os autovalores , e . Os autovetores de associados ao seu maior autovalor são da forma:
Ver solução completa
Questão 41
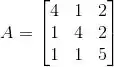
A dimensão do autoespaço de A associado ao autovalor 3 é:
(a) 0
(b) 1
(c) 2
(d) 3
Ver solução completaQuestão 42
Calcule os autovalores da matriz:
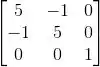
(a) 1, 2 e 6.
(b) 1, 3 e 7.
(c) 1, 4 e 6.
(d) 1, 3 e 5.
Ver solução completaQuestão 43
Calcule a soma dos módulos dos autovalores da matriz
a) 4
b)7
c) 6
d) 8
Ver solução completaQuestão 44
Uma matriz é conhecida parcialmente (apenas algumas de suas entradas):
Se , assinale um autovalor de :
Ver solução completa
Questão 47
Observe bem a matriz:
e marque a alternativa VERDADEIRA:
O núcleo de tem dimensão
A imagem de tem dimensão
possui dois autovalores iguais
é invertível
Ver solução completaQuestão 52
A matriz tem dois autovalores distintos. Um deles é 2.
(I) O outro autovalor é -2.
(II) O conjunto gerado pelos autovetores associados ao autovalor 2 tem dimensão 1.
(a) Ambas as afirmações são falsas.
(b) Ambas as afirmações são verdadeiras.
(c) (I) é verdadeira e (II) é falsa.
(d) (I) é falsa e (II) é verdadeira.
Ver solução completaQuestão 53
A soma dos MÓDULOS dos autovalores da matriz
é:
(a) 5
(b) 6
(c) 7
(d) 8
Ver solução completaQuestão 54
Seja fixado um sistema de coordenadas no plano, com
uma base ortonormal, e seja dado . Temos que a equação
Representa uma hipérbole se, e somente se:
