Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 5.Exercício - Ex. 3b

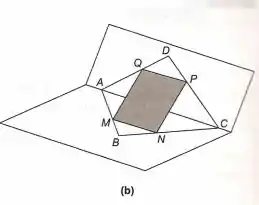
(b) No quadrilátero ABCD (eventualmente reverso, como na Figura 5-2 (b)), M divide (A,B), N divide (C,B), P divide (C,D) e Q divide (A,D), todos na razão r. Prove que o quadrilátero MNPQ é um paralelogramo.

Passo 1

Bora lá!

Esse é o nosso quadrilátero ACBD (eventualmente reverso), onde M divide (A,B), N divide (C,B), P divide (C,D) e Q divide (A,D), todos na razão r:

Antes de matarmos esse exercício, vamos relembrar o que ele nos pede:

Prove que o quadrilátero MNPQ é um paralelogramo.

Beleza? Então, partiu!

Passo 2

Do exercício resolvido 5-3, temos que:

A M → = r r + 1 A B →

Vamos provar isso?

De fato, pela definição de razão no qual um ponto divide um segmento:

A M → = r M B → → A M → = r ( M A → + A B → ) → A M → 1 + r = r A B → → A M → = r r + 1 A B →

Passo 3

De acordo com o enunciado, temos:

A M → = r M B → → M B → = 1 1 + r A B → C N → = r N B → → N B → = 1 1 + r C B →                     ( I )

O objetivo é mostrar que M N → é paralelo a A C → e determinar o seu módulo. Com isso, podemos escrever:

M N → = M B → + - 1 B N → = 1 r A M → + - 1 1 r C N → =

= 1 1 + r A B → - 1 1 + r C B → = 1 1 + r A B → + 1 1 + r B C → = 1 1 + r A C →                     ( I I )

Concluímos então que M N → // A C → 😉. Da mesma forma, podemos mostrar que Q P → / / A C → e determinar o seu módulo, certo?

Vamos lá!

Passo 4

Basta saber que

Q D → = 1 r A Q →   e   P D → = 1 r C P →

Logo, temos

Q P → = Q D → - P D → = 1 r A Q → - 1 r C P → = 1 1 + r A D → - 1 1 + r C D → =

= 1 1 + r A D → + D C → = 1 1 + r A C →           ( I I I )

De I I e I I I , temos que os vetores M N → e Q P → são equipolentes. E, pelas propriedades de equipolência de dois vetores, M N P Q é um paralelogramo.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Diz-se que o vetor v é combinação linear dos vetores v 1 ,v 2 ,...,v n quando se tem v=α 1 v 1+α 2 v 2+···+α n v n ,c o mα 1 ,α 2 ,...,α n∈R . Mostre que os vetores u ,vew são coplanares se, e somente
Calcule o cosseno do ângulo formado por duas diagonais de um cubo.
Sem usar coordenadas, explique o significado das seguintes afirmações: (a) os vetores u ,v são ortogonais; (b) o vetor v é ortogonal a reta r; (c) o vetor v é ortogonal ao plano Π ; (d) os vetores uev
Dados u=( α ,β ,γ ) , v=( α',β ',γ ') e w=( β γ '-γ β ',γ α '-α γ ',α β '-β α ') , calcule os produtos internos u , w ; v , w . Que relação entre u e v implica w = 0?
Sejam v 1 ,v 2ev 3 vetores não-coplanares. Se o vetor w é tal que w , v 1 = w , v 2 ≥ w , v 3 ≥ 0 , prove que w=0 .