Enunciado
Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 35.Problemas - Ex. 8
Seja f uma função que associa a cada matiz 3X3, cujas linhas são u, v e w um numero f(u,v,w) de tal modo que valham as propriedades 1,3 e 4 vistas acima para o determinante. Se f()= k, mostre que f(u, v, w ) = k det[u, v, w] para quaisquer u,v, w (Sugestão: escreva u =)
Passo 1
Fala galerinha , vamos resolver mais uma questão do nosso livro de Geometria analítica e Álgebra Linear !!!
Primeiramente vamos entender nosso problema.
É dito na questão que as funções serão,
f()= k
f(u, v, w ) = k det[u, v, w]
e cada componente dada pela função,
como é propostos na questão vamos encontrar o valor do determinante da função det[u, v, w]
+
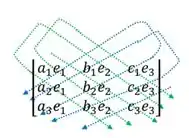
Com isso em mente, vamos então ao próximo passo...
Passo 2
Este passo será relembrar as propriedades citadas na questão,
Propriedade 1 o determinante muda de sinal quando realiza uma troca de posição entres as linhas,
Propriedade 3, se multiplicamos uma linha da matriz por número, o determinante fica multiplicado por aquele número.
Propriedade 4 se uma matriz é soma de duas parcelas vetoriais seu determinante é soma de dois outros, em cada um dos quais aquela linha é substituída por uma das parcelas.
=
disto isso, vamos para o próximo passo.
Passo 3
Agora vamos resolver, a multiplicação da função f() com uma matriz identidade
det[f() *] =*
det[f() *
det[f() *
é proposto que o valor de k é igual
Passo 4
Vamos agora calcular o valor do determinante apenas em função sem os coeficientes e ficando com,
+
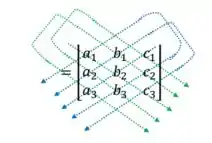
Passo 5
Galera como ultimo passo, vamor realizar a comparação entre os resultados das matriz,
+
+
Resposta
Então, podemos concluir e provar as propriedades citadas na questão,
+
f(u, v, w ) = k det[u, v, w]
Espero que ajudem nos estudos, até próxima