Determinantes

Fala aí, você chegou no Responde Aí! Aqui nós vamos bater um papo introdutório sobre determinantes de matrizes. Preparado? Então bora lá!

O que é determinante?

Nada mais lógico do que começarmos com a definição de determinantes, não é? hahaha

Um determinante nada mais é que uma função de em , ou seja, é uma função que pega elementos do espaço de matrizes quadradas e associa a esse elemento um número real.

Primeira coisa muito muito importante aqui: O determinante só está definido para matrizes quadradas. Percebe que pela definição, ele pega elementos do espaço de matrizes quadradas necessariamente. Guarda isso no coração, tá bom?

A notação que usamos para determinante são duas barrinhas, , no lugar dos colchetes, . Por exemplo, para essa matriz aqui:

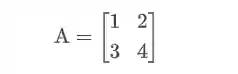
o determinante dela será denotado por:

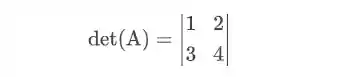
Como calcular determinantes?

Agora vamos começar a ver como calcular determinantes de matrizes. Existe uma fórmula chamada Teorema de Laplace que a gente pode usar pra calcular o determinante de qualquer matriz.

Porém, pras matrizes e existem maneiras mais fáceis e rápidas de calcular determinantes

Determinantes de Matriz

Para calcular determinantes de matrizes vamos usar a seguinte fórmula:

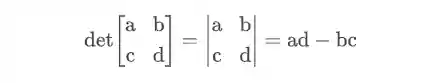
Por exemplo, o determinante da matriz abaixo:

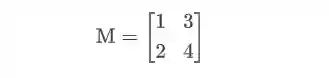
Será:

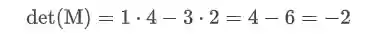
Bem simples, não é?

Determinantes de Matriz

Agora, para calcular determinante de matrizes temos que fazer umas coisinhas a mais. Vamos entender com um exemplo, que fica mais fácil, beleza?

Olha essa matriz aqui:

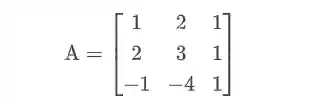
Vamos calcular o determinantes dela seguindo esse passo a passo aqui:

PASSO 1: Repetir as duas primeiras colunas ao lado do determinante

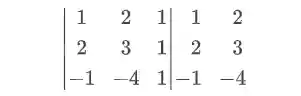
PASSO 2: Traçar linhas na diagonal principal e nas duas diagonais seguintes, indicando um sinal de em cima

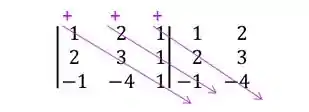
PASSO 3: Multiplicar os números de cada diagonal e somar os resultados dessa multiplicação

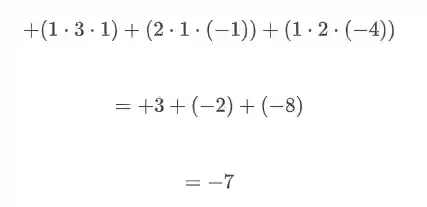
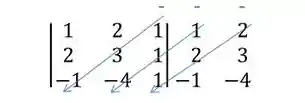
PASSO 4: Traçar linhas na diagonal secundária e nas duas diagonais seguintes, indicando um sinal de em cima

PASSO 5: Multiplicar os números de cada diagonal e somar os resultados dessa multiplicação

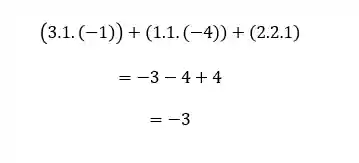
PASSO 6: Agora, para obeter o determinantes vamos pegar o resultado o passo e subtrair do resultado do passo .

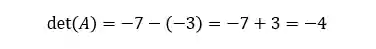
Obs.: Aquele sinal de menos que indicamos na diagonal secundária, no passo , é justamente pra indicar que vamos subtrair o resultado da multiplicação e soma das diagonais, beleza?

Tranquilo também, não é?

Videoaula

Se você quiser fixar essa introdução assistindo uma vídeo aula irada, é só conferir o vídeo que eu vou deixar aqui embaixo 👇🏽

Além disso, se você quiser aprofundar o seu estudo em determinantes é só conferir o nosso Raio-X aqui embaixo 👇🏽, onde temos todo o conteúdo que você precisa bem organizadinho para o seu estudo ser ótimo. 😉