Tem-se: , e e . O vetor é coplanar com e e .
- Determine as coordenadas de .
- Escreva como combinação linear de e .
Passo 1
- Fala, galerinha! Antes de começar, vamos relembrar que é coplanar com e e . A primeira afirmação quer dizer que , e são L.D. então , o determinante da matriz contendo esses três vetores deve ser nulo
- Agora temos que escrever como combinação linear de e . Para conseguir fazer isso, temos que fazer
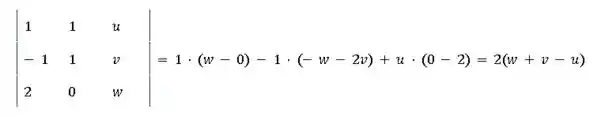
Assim,
Para conseguir determinar vamos utilizar a segunda informação do enunciado: . Isso quer dizer que e são L.D., ou seja,
Igualando as entradas dos vetores, obtemos o seguinte sistema de equações:
Agora, substituímos para obter . Voltando ao nosso vetor , obtemos
Passo 2
comparamos os dois lados e descobrimos o valor de e . Preparados? Então vamos lá!
Assim, temos o seguinte sistema de equações:
Substituindo na primeira equação, obtemos
Logo,