Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 1.Exercícios Propostos - Ex. 29

No triângulo ABC, P, Q e R são os pontos médios, respectivamente, de AB, BC, e AC. O ponto O é um ponto qualquer do espaço. Demonstre: O A   → +   O B   → +   O C →   =   O P →   +   O Q   → +   O R →   . (Sugestão: escreva O P → , O Q   → e O R   → em função de O A   → , O B   → e O C   → . )

Passo 1

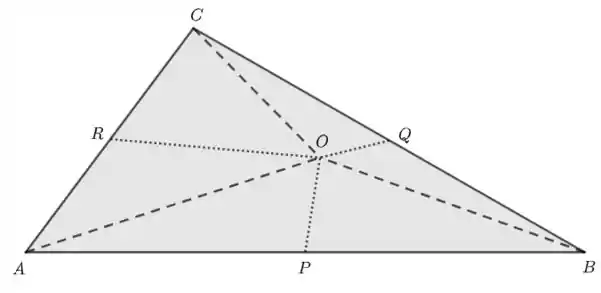
Vamos lá, para mostrar o que a questão pede, vamos primeiro desenhar um triângulo de um ponto qualquer O, que pode ser dentro ou fora do triângulo. Vai ficar mais ou menos como na figura abaixo, onde os segmentos tracejados indicam O A   → , O B   → e O C   → enquanto os segmentos pontilhados indicam O P → , O Q   → e O R → .

Passo 2

Seguindo a sugestão do livro, vamos escrever O P → , O Q   → e O R   → em função de O A   → , O B   → e O C → :

O P → = O B → + B P → = O B → + 1 2 B A →

O Q   → = O C   → + C Q   → = O C   → + 1 2 C B   →

O R   → = O A   → + A R   → = O A   → + 1 2 A C   →

Agora, somamos tudo e encontramos:

  O P →   +   O Q   → +   O R →   = O B → + 1 2 B A → + O C   → + 1 2 C B   → + O A   → + 1 2 A C   →

  O P →   +   O Q   → +   O R →     = O A   → +   O B   → +   O C →   + 1 2 B A → + 1 2 A C   → + 1 2 C B   →   =   O A   → +   O B   → +   O C →  

onde usamos o fato de que

1 2 B A → + 1 2 A C   → = 1 2 B C   → = - 1 2 C B   → ⇒ 1 2 B A → + 1 2 A C   → + 1 2 C B   → = 0 .

Resposta

Ver a resolução acima.

Exercícios de Livros Relacionados

Ache quatro pontos A, B, C e D no espaço, cujas coordenadas sejam 1 ou 0, de modo que ABCD seja um tetraedro regular. Verifique que duas arestas opostas desse tetraedro são ortogonais.
Dados os pontos distintos A = (a, b, c), A ′ = (a ′, b′, c′) e o número d0, mostre que existem, na reta AA′, 0, 1 ou 2 pontos P tais que d (O, P) = d. Se existir exatamente um ponto P com d (O, P) = d
Dado um triângulo acutângulo A B C , mostre que existe um ponto O no espaço, tal que os Ângulos A Ô B ,A Ô CeB Ô C Ô Ô Ô são retos. Determine as medidas das arestas e da altura da pirâmide de base A B
Prove que (u x v) x w + (v x w) x u + (w x u) x v = 0 .
Para quaisquer vetores u , v , w , prove que u x v , w=u , v x w .