Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Base e Dimensão

Ver Todos os Exercícios

Teoria

Vamos continuar falando sobre equações paramétricas e espaços gerados...

Será que todo conjunto de vetores que geram um espaço são uma base? O que um conjunto de vetores precisa ser para ser uma base?

Imagina que estamos no espaço R 3 e queremos definir o plano x y .

Nesse caso vamos chamar o plano x y de plano Π .

Posso representar Π através de vetores como já tínhamos estudado, por exemplo:

Π = s p a n { 1,0 , 0 ,   0,1 , 0 }

Certo?? Esses vetores geram o plano Π .

Quando multiplicamos esses vetores por um escalar, não alteramos a direção deles. Por exemplo, se multiplicarmos os vetores por 2 teríamos:

Π = s p a n { 2,0 , 0 ,   0,2 , 0 }

Esses novos vetores continuam a gerar Π .

Agora de somarmos esses dois vetores e acrescentarmos no s p a n também gerarmos o mesmo plano Π .

Π = s p a n { 1,0 , 0 ,   0,1 , 0 , ( 1,1 , 0 ) }

Ok, mas porque falei disso tudo? Desse jeito percebemos que adicionando um vetor combinação linear dos outros ou pegando múltiplos dos vetores anteriores, não altero o espaço que quero gerar. Vamos dar uma olhada nos gráficos pra conseguir ver isso melhor:

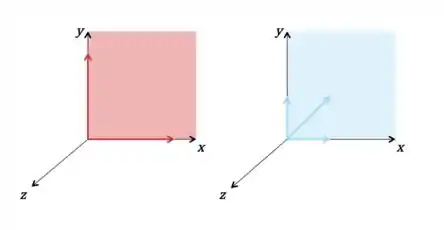
O primeiro representa o espaço gerado pelo conjunto { 2,0 , 0 ,   0,2 , 0 } e o segundo o espaço gerado pelo conjunto 1,0 , 0 ,   0,1 , 0 , 1,1 , 0 . Conseguem ver que são iguais? Ambos são o plano Π .

Podemos achar infinitos conjuntos que geram meu espaço. Vou dar mais alguns exemplos:

Π = s p a n { 4,0 , 0 ,   0,3 , 0 , ( 1,2 , 0 ) }

Π = s p a n { 1,0 , 0 ,   0,1 , 0 , 2,0 , 0 , ( 1,1 , 0 ) }

Deu pra entender né? Hahaha.

Nosso objetivo aqui é estudar alguns desses conjuntos que geram espaços: As Bases.

Base

Base é um conjunto de elementos do espaço vetorial. De Todos os exemplos lá de cima quais deles são bases?

Para ser uma Base, o conjunto de vetores precisam seguir duas regras:

  • Gerar o espaço
  • Ser LI

Ou seja, as bases são os conjuntos Linearmente Independentes de vetores que geram o espaço!

Por exemplo:

1,0 , 0 ,   0,1 , 0 é um conjunto de vetores LI que geram o plano Π , logo é uma base!

O mesmo acontece com { 2,0 , 0 ,   0,2 , 0 } também é uma base de Π .

Se olharmos para 1,0 , 0 ,   0,1 , 0 , ( 1,1 , 0 ) } temos que o vetor ( 1,1 , 0 ) que é uma combinação linear dos dois primeiro logo LD. Então { 1,0 , 0 ,   0,1 , 0 , ( 1,1 , 0 ) } não é uma base de Π apesar de gerar o espaço , como vimos anteriormente.

Dimensão

Todo espaço é gerado por um número mínimo de elementos. Ao número mínimo de vetores que geram um espaço damos o nome de dimensão do espaço. Por exemplo:

Vamos voltar lá a um dos conjuntos geradores do plano x y :

Π = s p a n { 1,0 , 0 ,   0,1 , 0 }

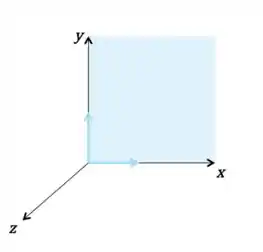
Vemos que com 2 vetores consigo gerar o plano que eu quero.

Agora e se eu adicionar um vetor?

Π = s p a n { 1,0 , 0 ,   0,1 , 0 , ( 1,1 , 0 ) }

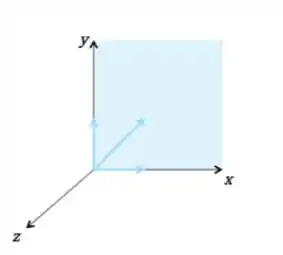
Conseguimos ver que com 3 vetores o espaço que eu gero continua o mesmo!

E se eu tirar dois vetore?

Π = s p a n { 1,0 , 0 }

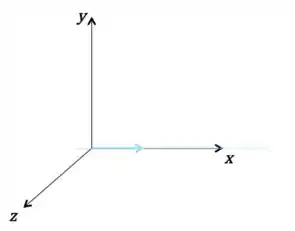
Opa!! Agora, com 1 vetor, meu espaço já não é o mesmo. Não consigo gerar o plano x y com apenas 1 vetor, gero apenas o eixo x .

Conseguiram entender agora? O número mínimo para gerar o plano Π é 2 . Falamos que a dimensão desse espaço é 2 :

d i m = 2

Tá mas pra que serve isso? E se eu te perguntar se o conjunto { 1,2 , 0 ,   0,0 , 3 , ( 0,1 , 3 ) } é base do R 3 ?

Conseguimos descobrir facilmente que é um conjunto L I   mas será que é um conjunto gerador de R 3 ? O que um conjunto precisa para ser conjunto gerador? Se descobrimos qual a dimensão do espaço podemos saber qual o número mínimo de vetores para se ter uma base.

O espaço R 3 tem dimensão 3. Logo para se ter uma base, precisamos de no mínimo três vetores linearmente independentes.

Esse meu conjunto   { 1,2 , 0 ,   0,0 , 3 , ( 0,1 , 3 ) } é LI e também tem 3 elementos então é uma base de R 3 .

Lembrando que se eu tiver mais que isso, continuo tendo um conjunto gerador, mas não vai ser uma base pois algum vetor vai ser necessariamente uma combinação linear dos outros.

Uma outra forma de pensar em dimensão é como o número de vetores na base de um espaço!

Agora, pra terminar, vamos aprender umas coisas importantes sobre base e dimensão:

  • Espaços compostos por polinômios e matrizes também tem bases e portanto dimensões.
  • A base canônica de um espaço é aquela mais “simples”. Por exemplo, no R 2 é essa: { 1,0 , 0,1 } formada apenas por 1 ' s e 0 ' s , os próprios vetores dos eixos.
  • Não podemos ter um espaço de maior dimensão que o próprio espaço em que os vetores geradores estão contidos. Por exemplo, não conseguimos gerar nenhum espaço de dimensão maior que 3 com vetores do R 3 ,ou seja, com 3 coordenadas.

Base

Dimensão

Agora, pra terminar, vamos aprender umas coisas importantes sobre base e dimensão:

Exercícios Resolvidos

Exercício Resolvido #1

Alfredo Steinbruch e Paulo Winterle Álgebra Linear , 2 a ed., São Paulo, Pearson, 1987, pp. 97 – Ex. 66

Determinar uma base do subespaço do R 4 gerado pelos vetores v 1 = 1 , - 1,0 , 0 ,     v 2 = - 2,2 , 2,1 ,   v 3 =   ( - 1,1 , 2,1 ) e v 4 = ( 0,0 , 4,2 )

Passo 1

Bom, nós temos um conjunto gerador do espaço no qual queremos achar a base, e qual a diferença entre a base e um conjunto gerador??

A base é um conjunto L I !

Assim, basta que a gente transforme aquele conjunto { v 1 ,   v 2 ,   v 3 ,   v 4 } em L I , retirando os vetores C L dos outros, escalonando. Então primeiro, vamos botá-los nas linhas da uma matriz:

1 - 2 - 1 0 - 1 2 1 0 0 2 2 4 0 1 1 2

Passo 2

E agora escalonar:

1 - 2 - 1 0 - 1 2 1 0 0 2 2 4 0 1 1 2   → L 2 ← L 2 + 2 L 1 L 3 ← L 3 + L 1 1 0 0 0 - 1 0 0 0 0 2 2 4 0 1 1 2

1 0 0 0 - 1 0 0 0 0 2 2 4 0 1 1 2 → L 3 ← L 3 - L 2 L 4 ← L 4 - 2 L 2 1 0 0 0 - 1 0 0 0 0 2 0 0 0 1 0 0

As duas últimas linhas foram zeradas, mostrando que v 3 e v 4 eram C L de v 1 e v 2 !

Assim, retirando esses dois vetores do conjunto, temos uma base para o espaço que ele gera:

{ 1 , - 1,0 , 0 , - 2,2 , 2,1 }

Resposta

{ v 1 , v 2 }

Exercício Resolvido #2

UFRJ, Álgebra Linear, P1 – 2017.1, Questão 15

Determine a dimensão do conjunto abaixo:

( 1 ,   - 1 ,   1 ,   - 2 ) , ( 1 ,   0 ,   3 ,   - 1 ) , ( 1 ,   - 1 ,   0 ,   - 5 ) , ( 1 ,   0 ,   4 ,   2 )

(a) 3

(b) 4

(c) 1

(d) 2  

Passo 1

A dimensão é o numero de vetores na base, porém para ser base é preciso que o conjunto de vetores seja   L I . Dessa forma, temos que ver se tem vetores C L ’s dos outros nesse conjunto:

( 1 ,   - 1 ,   1 ,   - 2 ) , ( 1 ,   0 ,   3 ,   - 1 ) , ( 1 ,   - 1 ,   0 ,   - 5 ) , ( 1 ,   0 ,   4 ,   2 )

Vamos escalonar:

1 1 1 1       - 1 0 - 1 0       1 3 0 4       - 2 - 1 - 5 2 → L 2 → L 2 - L 1 L 3 → L 3 - L 1 L 4 → L 4 - L 1 1 0 0 0       - 1 1 0 1       1 2 - 1 3       - 2 1 - 3 4 → L 4 → L 4 - L 2 1 0 0 0       - 1 1 0 0       1 2 - 1 1       - 2 1 - 3 3

→ L 4 → L 4 + L 3 1 0 0 0       - 1 1 0 0       1 2 - 1 0       - 2 1 - 3 0

Uma linha zerou, logo apenas 3 dos 4 vetores formam a base do espaço, portanto a dimensão dele vai ser igual a 3

Resposta

a

Exercício Resolvido #3

UFRJ, Álgebra Linear, P1 – 2017.1, Questão 10

Assinale o vetor que adicionado ao conjunto { ( 1,2 , 3 ) , ( 2,4 , 9 ) } forma uma base para o R 3 :

(a) ( 0 ,   0 ,   6 )

(b) ( 3 ,   6 ,   12 )

(c) ( 6 ,   - 3 ,   0 )

(d) ( 1 ,   2 ,   6 )

Passo 1

Para formar a base do R 3 , o vetor precisa simplesmente não ser C L dos outros 2.

Vamos testar as afirmativas escalonando, lembrando que se uma linha zerar quer dizer que o vetor que estava nela é combinação linear dos demais.

(a) ( 0 ,   0 ,   6 )

1 2 3 2 4 9 0 0 6 → L 2 → L 2 - 2 L 1 1 2 3 0 0 3 0 0 6 → L 3 → L 3 - 2 L 2 1 2 3 0 0 3 0 0 0

Zerou!! Não é esse!!

(b) ( 3 ,   6 ,   12 )

1 2 3 2 4 9 3 6 12 → L 2 → L 2 - 2 L 1 L 3 → L 3 - 3 L 1 1 2 3 0 0 3 0 0 3 → L 3 → L 3 - L 2 1 2 3 0 0 3 0 0 0

Zerou de novo!! Não é esse!!

(c) ( 6 ,   - 3 ,   0 )

1 2 3 2 4 9 6 - 3 0 → L 2 → L 2 - 2 L 1 L 3 → L 3 - 6 L 1 1 2 3 0 0 3 0 - 15 - 18 → L 1 ↔ L 3 1 2 3 0 - 15 - 18 0 0 3

Não zerou! Podemos parar por aqui, porque esse vetor vai ser nossa resposta.

Resposta

c

Exercício Resolvido #4

UFRJ, Álgebra Linear, P1- 2015.1, Questão 03

Assinale a alternativa CORRETA:

( a ) 1,0 , 1,1 , 1 , - 1 não é um conjunto gerador de R 2

( b ) 1,0 , 0,1 e 1,1 , 1 , - 1 são bases de R 2

( c ) 1,1 , 1 , 2,2 , 2 , 3,3 , 3 é um conjunto gerador de R 3

( d ) 1,2 , 3 , 4,5 , 6 , 7,8 , 9 é uma base de R 3

Passo 1

Letra a

Incorreta! De fato, o conjunto não é base de R 2 já que tem 3 elementos. Mas como temos dois elementos L I , ele gera o R 2 !

Só podemos afirmar isso porque é um conjunto de vetores do R 2 (duas coordenadas), não são quaisquer dois vetores L I que formam o R 2 não em! Isso confunde muita gente.

Letra b

Certa a resposta! Temos dois conjuntos formados por 2 vetores L I do R 2 , então naturalmente eles são bases do R 2 .

Letra c

Não!! Cara, todos os vetores são múltiplos, isso aí forma só uma reta haha. Incorreta.

Letra d

Incorreta. Então, essa matriz aí do 1 ao 9 já é meio manjada haha. Se você não viu ela ainda eu já te aviso que as linhas dela são L D , então não vai ser uma base do R 3 ! Quer ver?

1 2 3 4 5 6 7 8 9 → L 2 ← L 2 - 4 L 1 L 3 ← L 3 - 7 L 1 1 2 3 0 - 3 - 6 0 - 6 - 12 → L 3 ← L 3 - 2 L 2 1 2 3 0 - 3 - 6 0 0 0

Resposta

Letra ( b )

Exercício Resolvido #5

Anton e Rorres, Álgebra Linear com Aplicações, 8ª Ed., Porto Alegre, Bookman, 2005, pp. 183 – ex. 18

Determine as dimensões dos seguintes subespaços de R 4 .

  1. todos os vetores da forma ( a ,   b ,   c ,   0 )
  2. todos os vetores da forma a , b ,   c ,   d , onde d = a + b e c = a - b
  3. todos os vetores da forma a ,   b ,   c ,   d , onde a = b = c = d

Passo 1

Vamos começar isso aí, primeiro pela letra (a):

Queremos a dimensão do subespaço cujos vetores tem a forma   ( a ,   b ,   c ,   0 ) .

Bom, dimensão é o número de vetores presentes na base do espaço, então vamos tentar achar uma base para esse espaço aí!

Temos 3 variáveis livres, certo, posso escrever esses vetores dessa forma:

a ,   b ,   c , 0 = a 1 ,   0 ,   0 ,   0 + b 0 ,   1 ,   0 ,   0 + c ( 0 ,   0 ,   1 ,   0 )

Logo, a base desse espaço vai ser { 1 ,   0 ,   0 ,   0 , 0 ,   1 ,   0 ,   0 ,   0 ,   0 ,   1 ,   0 }

Como tem 3 vetores, a dimensão será 3!

Um bizú: o número de variáveis livres é igual a dimensão do espaço, então nem precisaríamos achar essa base e decompor o vetor para achar nossa resposta, o que facilita muito nossa vida!!

Passo 2

Vamos agora para a letra (b):

Bora analisar a dimensão do subespaço cujos vetores tem a forma a , b ,   c ,   d , onde d = a + b e c = a - b :

Com o bizú que vimos ali em cima, percebemos que nosso novo objetivo é achar o número de variáveis livres.

Temos 4 variáveis no nosso vetor, porém 2 delas estão em função das outras o que as torna variáveis dependentes, sobrando então, 2 variáveis livres.

Assim, nosso espaço tem dimensão 2!

E por último a letra (c):

Queremos agora a dimensão do subespaço de vetores a ,   b ,   c ,   d , onde a = b = c = d .

Bom, essa aqui fica mais fácil de visualizar substituindo os valores no vetor. Como a = b = c = d , temos:

a ,   b ,   c ,   d = ( a ,   a ,   a ,   a )

Ou seja, temos apenas uma variável livre! E portanto, um espaço de dimensão 1.

Resposta

  1. 3
  2. 2
  3. 1

Exercício Resolvido #6

Elaboração própria.

Determine o valor de m para que o conjunto B forme uma base para M 2 x 2 ( R ) .

B = 2 0 0 2 ,   0 3 0 0 ,   0 1 m 0 ,   0 0 0 1

Passo 1

Beleza, a gente tem um conjunto B com 4 matrizes e queremos o valor de m pra que essas matrizes sejam base de M 2 x 2 ( R ) .

Antes de tudo, uma base composta por matrizes 2 x 2 tem sempre dimensão 4, então no caso já estamos de acordo com isso, pois temos 4 matrizes.

Agora nossa condição é que essas 4 matrizes sejam L.I., para isso:

α 2 0 0 2 + β 0 3 0 0 + γ 0 1 m 0 + δ 0 0 1 1 = 0 0 0 0 → α = β = γ = δ = 0

Passo 2

Da equação do passo 1, temos

2 α 0 0 2 α + 0 3 β 0 0 + 0 γ m γ 0 + 0 0 1 δ 1 δ = 0 0 0 0

Somando as matrizes:

2 α 3 β + γ m γ + δ 2 α + δ = 0 0 0 0

Agora vamos igualar termo a termo:

2 α = 0 3 β + γ = 0 m γ + δ = 0 2 α + δ = 0

Passo 3

Queremos que nosso conjunto seja L.I, então devemos ter que α = β = γ = δ = 0 :

2 . 0 = 0 3 . 0 + 0 = 0 m . 0 + 0 = 0 2 . 0 + 0 = 0

0 = 0 0 = 0 m . 0 = 0 0 = 0

Beleza, isso condiz pra todas as outras equações, mas e na linha de m , qual deve ser o valor dele pra que m . 0 = 0 ??

Isso aí, m pode assumir qualquer valor, afinal, vai ter um 0 multiplicando ele ali certo?

Então, basicamente, pra qualquer valor de m , o conjunto B = 2 0 0 2 ,   0 3 0 0 ,   0 1 m 0 ,   0 0 0 1 vai ser L.I :)

Resposta

m pode assumir qualquer valor.

Exercício Resolvido #7

UFSC – Exercícios de base e dimensão.

Os vetores x 1 = 1 2 2 , x 2 = 2 5 4 , x 3 = 1 3 2 , x 4 = 2 7 4 , x 5 = 1 1 0 geram R 3 .

Retire algum (ou alguns) elementos de { x 1 ,   x 2 ,   x 3 ,   x 4 ,   x 5 } de modo a obter uma base para R 3 .

Passo 1

Como queremos uma base para R 3 , devemos tirar 2 vetores de { x 1 ,   x 2 ,   x 3 ,   x 4 ,   x 5 } , de modo a ficarmos com apenas 3 vetores e assim termos dimensão 3, como desejado ok?

Os 3 vetores que vão ficar no conjunto devem, necessariamente, ser L.I., pois queremos que eles formem uma base certo?

Lembrando que pra um conjunto de vetores serem LI é necessário que

α 1 x 1 + α 2 x 2 + … = 0

Somente se TODOS os coeficientes forem 0. Se umzinho for diferente de zero então o conjunto é LD.

Passo 2

Vamo fazer uma estratégia aqui! Primeiro vamos pegar dois vetores que sejam LI entre si, assim nós vamos ter R 2 . A partir daí a gente pega um terceiro vetor pra e aí verificamos se os 3 são LI.

Vamos pegar o primeiro e segundo

α 1 x 1 + α 2 x 2 = 0

α 1 1 2 2 + α 2 2 5 4 = 0 0 0

Que nos dá as seguintes equações

α 1 + 2 α 2 = 0

2 α 1 + 5 α 2 = 0

2 α 1 + 4 α 2 = 0

A primeira e terceira equação até concordam entre si, né? Mas botando a segunda equação na história a única solução possível é α 1 = α 2 = 0 . Isso significa que esses dois vetores são LI

Passo 3

Agora vamos colocar o vetor x 3 e ver o que acontece

α 1 x 1 + α 2 x 2 + α 3 x 3 = 0

α 1 1 2 2 + α 2 2 5 4 + α 3 1 3 2 = 0 0 0

Montando o sistema de equações pra esse caso vamos ter

α 1 + 2 α 2 + α 3 = 0

2 α 1 + 5 α 2 + 3 α 3 = 0

2 α 1 + 4 α 2 + 2 α 3 = 0

Olhando pra esse sisteminha, vemos que a terceira equação é igual a primeira (só que multiplicada por 2). Isso nos dá um sistema com 2 equações e 3 variáveis, então no melhor caso possível o sistema tem uma solução com um parâmetro livre.

Então não temos só uma solução com todos parâmetros nulos, o que significa que esses vetores são LD

Passo 4

Agora vamos usar o vetor x 4

α 1 x 1 + α 2 x 2 + α 3 x 4 = 0

α 1 1 2 2 + α 2 2 5 4 + α 3 2 7 4 = 0 0 0

O que nos dá o seguinte sistema

α 1 + 2 α 2 + 2 α 3 = 0

2 α 1 + 5 α 2 + 7 α 3 = 0

2 α 1 + 4 α 2 + 4 α 3 = 0

Aconteceu a mesma coisa do passo anterior, né? A terceira equação é duas vezes a primeira, então esse conjunto é LD também :/

Passo 5

Então vamos pro quinto vetor

α 1 x 1 + α 2 x 2 + α 3 x 5 = 0

α 1 1 2 2 + α 2 2 5 4 + α 3 1 1 0 = 0 0 0

O que nos dá o seguinte sistema de equações

α 1 + 2 α 2 + α 3 = 0

2 α 1 + 5 α 2 + α 3 = 0

2 α 1 + 4 α 2 = 0

Da terceira equação

α 1 = - 2 α 2

Jogando na primeira equação

- 2 α 2 + 2 α 2 + α 3 = 0 → α 3 = 0

Jogando esses dois resultados na primeira

2 - 2 α 2 + 2 α 2 + 0 = 0 → - 2 α 2 = 0 → α 2 = 0

Voltando para α 1

α 1 = 0

A única solução do nosso sistema é que todos os parâmetros são zero! Isso significa que esse conjunto é LI! Uhullll! Achamos :D

Resposta

{ x 1 ,   x 2 ,   x 5 }

Exercício Resolvido #8

Universidade Federal do Paraná, Lista de Álgebra Linear, Olivier Brahic

Encontre uma base para o subespaço S de R 4 consistindo em todos os vetores da forma ( a + b ,   a - b + 2 c ,   b ,   c ) , nos quais a , b e c são números reais. Qual é a dimensão de S ?

Passo 1

Queremos vetores que possam ser escritos como a + b ,   a - b + 2 c ,   b ,   c .

Vamos separar esse vetor em partes para encontrarmos seus geradores:

a + b ,   a - b + 2 c ,   b ,   c = a ,   a ,   0 ,   0 + b ,   - b ,   b ,   0 + ( 0 ,   2 c ,   0 ,   c )

Passo 2

Colocando para fora dos vetores as nossas variáveis a , b e c :

a 1 ,   1 ,   0 ,   0 + b 1 ,   - 1 ,   1 ,   0 + c ( 0 ,   2 ,   0 ,   1 )

Seja o conjunto de geradores { 1 ,   1 ,   0 ,   0 ,   1 ,   - 1 ,   1 ,   0 ,   0 ,   2 ,   0 ,   1 } , de fato todos eles são escritos da forma a + b ,   a - b + 2 c ,   b ,   c , agora vamos verificar se eles são L.I. para que sejam base de R 4

Passo 3

Seja:

α 1 ,   1 ,   0 ,   0 + β 1 ,   - 1 ,   1 ,   0 + γ 0 ,   2 ,   0 ,   1 = 0

α ,   α ,   0 ,   0 + β ,   - β ,   β ,   0 + 0 ,   2 γ ,   0 ,   γ = 0

Isso nos dá:

α + β = 0 α - β + 2 γ = 0 β = 0 γ = 0

Daí, temos que α = β = γ = 0 . Logo, nossos 3 vetores são L.I e então formam uma base para S :)

Como temos 3 vetores, S tem dimensão 3 ok?

Lembrando que não existe apenas um conjunto de geradores viu? Se você encontrou outro, pode estar certo também!!

Você também poderia selecionar 3 vetores quaisquer escritos na forma a + b ,   a - b + 2 c ,   b ,   c e verificar se são L.I.

Resposta

{ 1 ,   1 ,   0 ,   0 ,   1 ,   - 1 ,   1 ,   0 ,   0 ,   2 ,   0 ,   1 }

S tem dimensão 3.