Espaços Gerados
Produzido por Bruno PestanaTeoria
Interpretação geométrica
Bom, já aprendemos sobre equações cartesianas e paramétricas, agora vamos falar um pouquinho sobre o que elas fazem. Vamos dar uma olhada nessa equação da reta e nessa do plano :
Repare na reta que o vetor é o vetor diretor, ou seja, ele é o responsável por dar direção a nossa reta, por isso, podemos dizer que ele gera a reta , mas não só ele! Ela é gerada por ele e todos os seus múltiplos, pois são todos os . Já o vetor deslocamento não influencia na direção ou “tamanho” da reta, ele só a tira da origem.
Agora repare no plano , este agora não possui um vetor gerador apenas. Podemos dizer que esse plano é um espaço gerado pore . Novamente, o vetor deslocamento não influencia no “tamanho” do plano, quem faz isso são os parâmetros e . Mas então os geradores são todos os múltiplos dee ?? Vamos chamar de e de e olhar a imagem:
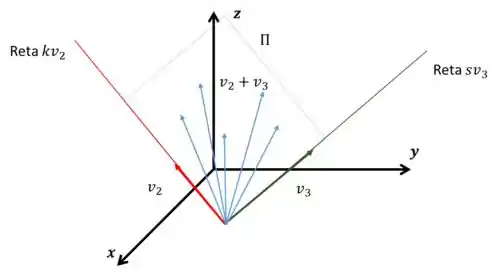
Repare os vetores e geram as retas e respectivamente. E sabemos que estes vetores também geram o plano . Vamos voltar à nossa pergunta: o que significa ser gerado por todos os múltiplos de e ??
Perceba que se pegarmos apenas , ou seja, teríamos o vetor um dos vetores azuis da imagem acima, mas ainda não seria suficiente. O necessário, então, seria pegar infinitos múltiplos de e somarmos com infinitos múltiplos de , e o que é isso? Combinação Linear!! Então estamos simplesmente fazendo infinitas combinações de e por exemplo: etc.
Blz, então faríamos isso até “preenchermos” o plano com todos aqueles vetores azuis (lembre-se que ele é infinito). Mas eu posso simplesmente pegar os múltiplos assim? Sim!! Porque na verdade eles já estão representados na equação pelos parâmetros multiplicando os vetores diretores!!
Então, na verdade, o plano é formado por .
Definição
Acho que já sabemos mais ou menos o que é um espaço gerado, vamos ver a definição formal ai rapidinho:

No fundo, um espaço gerado é apenas a combinação linear de um bando de vetores.
Antes de avançarmos, fica ligado em algumas informações importantes que fiz especialmente pra você:
Obs1.: Também podemos denotar o espaço gerado pelo conjunto como . Vou alternar entre as duas formas nas teorias e exercícios pra vocês não ficarem acostumados com uma só e se esquecerem da outra haha.
Obs2.: o sempre terá espaços geradores na origem. Podemos perceber isso notando que não há o vetor deslocamento quando fazemos um de algum conjunto. Apenas aparecem parâmetros multiplicados por vetores.
Espaços Gerados diferentes, só que não
Existe um plano gerado por ?
Bom, se fizermos , podemos ver que estamos apenas somando os múltiplos de vetores na mesma direção e assim não podemos “preencher” o plano. Assim poderíamos resumir esse a apenas:
E podemos concluir que:
Isso acontece porque temos um vetor que é combinação linear do outro! (No caso, se trata apenas de dois vetores e podemos dizer que eles apenas são múltiplos). É a mesma ideia da parametrização e das equações redundantes lembra?
Vamos ver outro exemplo com mais vetores.
Se liga nesse espaço gerado ai embaixo:
Reparou que o vetor do meio é:
Ou seja, ele é uma dos outros dois vetores, então podemos desconsiderar ele do nosso espaço gerado e, portanto, ele não influencia em nada no “formato” do espaço gerado, sacou? Só seguir a mesma ideia de parametrização.
Logo, podemos dizer que:
Então, sempre quando tivermos um vetor que é uma dos demais, podemos tirá-lo do espaço gerado.
Vetores pertencentes a um espaço gerado
Ex:
Será que o vetor pertence ao plano ?
Como um espaço gerado é a combinação linear de um bando de vetores, podemos mudar a pergunta para: Será que o vetor é uma combinação linear de ?
Agora ficou fácil não? Basta fazer:
Viu que encontramos dois valores para ? Então, quer dizer que o sistema é impossível e não admite solução, ou seja, não tem nenhum valor real para que satisfaça a equação. Sendo assim, o vetor não pertence ao espaço gerado.
Ex:
Será que , por exemplo, pertence a ? Ou, mais geometricamente, o vetor está contido no plano gerado por ??
Bom, para isso, deve ser da forma . Só que isso é impossível, já que o último componente do vetor deveria ser , quando, na verdade, o último componente é . Logo, não pertence ao espaço gerado. Podemos perceber que o vetor não pertence ao plano gerado por e . Tente visualizar!
Ex:
A última aqui pra termina eu juro. Se eu quiser saber se uma reta gerada pelo vetor pertence ao plano . Repare que se é a reta, estamos nos referindo a . Caramba como vou verificar se um pertence ao outro??? Vamos olhar para o vetor diretor, pois se ele pertence ao plano, todos os seus múltiplos também pertencem não é mesmo??
ERRADO!! Olha só:
Vamos olhar para o vetor diretor da reta somente. Quando pensamos que um vetor pertence a um plano, acho que essa é a imagem que vem a sua cabeça:
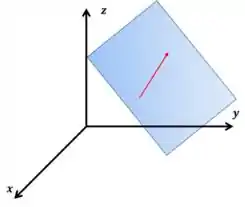
Se não, muito bom pra você. Mas eu disse nos capítulos anteriores que o vetor é a pontinha da nossa seta, tá lembrado? Sendo assim, quando ocorrer o caso da imagem acima, dizemos que o vetor é paralelo ao plano.
Mas e o vetor deslocamento, ele toca apenas em um ponto do plano, não é mesmo?
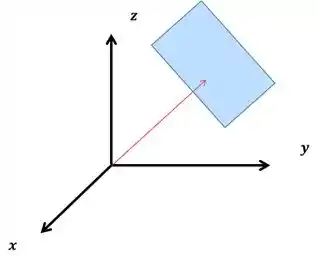
E como a ponta da flecha é o vetor, então ele pertence ao plano.

Repare agora outra coisa, o vetor diretor da reta é exatamente o vetor deslocamento do plano! Sendo assim, se tivéssemos testado se de fato seria verdade, mas como se trata de uma reta, os outros múltiplos também precisam estar dentro do plano!
Mas como ele toca o plano em um ponto apenas, qualquer múltiplo que você multiplique estará aumentando ou diminuindo vetor e ,consequentemente, perfurando ou deixando de tocar no plano, sacou? Então, tome cuidado quando se tratar de espaços deslocados!
Para a sua (ou nossa) alegria,

Quando se tratar de espaços não deslocados, não será necessária essa contarada toda, pois se eles pertencerem serão paralelos ao espaço também, já que ambos tem que passar pela origem. Nunca vai dar pra tangenciar o espaço.
Definição
Espaços Gerados diferentes, só que não
Vetores pertencentes a um espaço gerado
Exercícios Resolvidos
Exercício Resolvido #1
Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 23 – Fix. 1.10
Determine se é ponto, reta ou plano.
Passo 1
Letra a)
Podemos ver que dentro do espaço gerado, possui dois vetores que formam um conjunto .
Isso por que o segundo vetor é duas vezes o primeiro
Então isso aqui é uma reta.
Letra b)
Já nessa letra, os vetores do espaço gerado são , pois não são múltiplos.
Então é um plano no .
Letra c)
Como temos apenas um vetor não nulo, o espaço gerado por isso é uma reta.
Letra d)
Trata-se deum ponto, pois o espaço gerado pelo vetor nulo não gera nada ;)
Resposta
- Reta
- Plano
- Reta
- Ponto
Exercício Resolvido #2
Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 24 – Prob 1.15
Determine se:
Passo 1
Na letra , temos o espaço gerado , que é gerado por todas as combinações lineares de , ou seja, todos os seus múltiplos! Mas o não é múltiplo de , pois não pode ser escrito na forma . Logo ele não pertence ao espaço gerado, e a afirmativa é falsa.
Passo 2
Na , é só você ver se o é combinação linear dos outros (lembre-se que é a mesma coisa que Assim:
Igualando:
As duas últimas equações são iguais! Então é só fazer e substituir, aí temos:
Se , então . Então temos:
Como de fato é combinação linear dos outros dois, então ele pertence ao espaço gerado por eles e a afirmativa é verdadeira.
Passo 3
A é quase igual à , então vamos fazer a mesma coisa:
Igualando:
Iiiiih! A segunda e a terceira equação se contradizem! Isso quer dizer que o não é combinação linear dos outros! Assim, ele também não pertence ao espaço gerado, e a afirmativa é falsa.
Passo 4
Letra
Bom, pela localização dos zeros podemos ver que nenhum vetor é combinação linear um do outro. E como também possuem três coordenadas formam uma base para o . Assim, a afirmativa é verdadeira
Passo 5
Para o espaço gerado por ser igual ao espaço gerado por eles devem ter as mesmas combinações lineares, logo os mesmos múltiplos. Assim, eles devem ser múltiplos um do outro! E como eles não são múltiplos um do outro, a afirmativa é falsa.
Resposta
F, V, F, V, F
Exercício Resolvido #3
Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 24 – Prob. 1.12 a), b), c)
Considere o plano . Determine:
Quatro pontos distintos de
Se
Se
Passo 1
Letra
Bom, como se trata da equação paramétrica de um plano, basta estipularmos valores para seus parâmetros para conseguirmos os pontos.
Para :
Para :
Para :
Para :
Tranquila essa.
Passo 2
Letra
Para verificar se um ponto pertence ao plano, basta igualar a parametrização do plano:
Como temos duas equações repetidas, vamos descartá-las:
Sendo assim, como achamos valores reais para nossos coeficientes podemos dizer que o ponto pertence ao plano para .
Passo 3
Letra
Vamos seguir o mesmo procedimento da letra
Percebe só, que achamos dois pares de equações diferentes? Duas equações não podem ter valores diferentes! Sendo assim, o sistema não tem solução. Se está em dúvida tente fazer os cálculos para achar e depois não se esqueça de substituir os valores em TODAS as equações, e não somente as que você usou para achar tais valores.
Resposta
Sim, para
Não pertence
Exercício Resolvido #4
Lista de Monitoria 1 de Álgebra Linear da P1, Questão 2, 2015.1 PUC-rio (Adaptado)
Seja o plano , tal que sua equação paramétrica é:
Decida se é Verdadeiro ou Falso e justifique:
- A reta gerada pelo vetor intersecta
- Se , então para todo
Passo 1
Vamos começar pela primeira bolinha: a reta gerada pelo vetor intersecta ?
Bom, sabemos que uma reta é gerada por todos os múltiplos (ou ’s ) do seu vetor diretor. Então, poderiamos escrevê-la como:
Passo 2
Agora basta igualar as equações paramétricas:
Passo 3
Pela e , podemos ver que , assim vamos substituir na !
Logo, . Assim, podemos ver que a reta gerada pelo vetor intersecta o plano , quando e . Então, o primeiro item é VERDADEIRO.
Passo 4
A segunda é muito fácil! Sem fazer contas você já consegue visualizar que o plano é deslocado pelo vetor , assim ele não está na origem. Então este item é FALSO. Qualquer dúvida, tente igualar o vetor nulo a equação paramétrica do plano e achar se existem ... você verá que não existe!
Passo 5
Para a terceira afirmação, vamos seguir a mesma ideia do primeiro item, ou o que você faria no item anterior se tivesse com dúvida.
Agora basta substituir na primeira equação e verificamos que:
Então, de fato, o vetor pertence ao plano. Logo, o terceiro item é VERDADEIRO.
Passo 6
Este último item é um pouco mais difícil, tenho que admitir. De imediato você pensaria que a resposta é verdadeiro, né? Porque a noção de pertencer ao plano que todos nós temos é esta aqui:
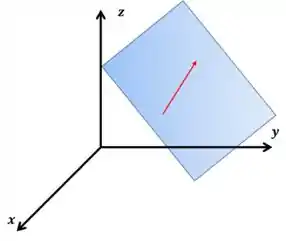
Entretanto, não é sempre isso que acontece. Lembra do vetor deslocamento?
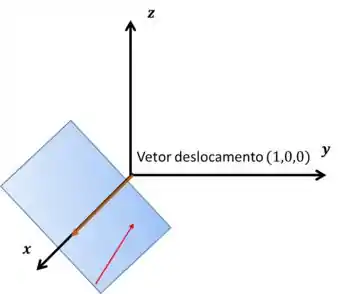
Perceba que se o vetor deslocamento “esticar” um pouco, ele vai “furar” o plano, por causa de um simples detalhe: o vetor não é a flecha inteira, apenas a pontinha da flecha! Mudou sua vida não, rs? Quando descobri isso, a minha mudou.
Não ta acreditando? Tente esticar o vetor deslocamento. Por exemplo, multiplique por e resolva o sistema!
O mesmo podemos aplicar para o vetor : tente multiplicá-lo por e ver se pertence ao plano (você verá que não). Logo, o item é FALSO.
Resposta
V, F, V, F
Exercício Resolvido #5
Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 85 – Fix. 3.6
Se o espaço gerado por é igual ao espaço gerado por , então necessariamente _________ ( é múltiplo de é perpendicular a , nenhuma das alternativas)
Se , então necessariamente _____ ( é múltiplo de , é perpendicular a , nenhuma das alternativas)
Passo 1
Letra
Como o espaço gerado, é o espaço criado por todos os múltiplos daquele vetor (quando se trata de vetor), então não importa o múltiplo do vetor que pegarmos, pois no final teremos sempre todos os múltiplos dele. Logo a opção correta é é múltiplo de
Letra
Agora como se trata de dois vetores, não podemos mais falar que um é múltiplo do outro. No caso, para o espaço gerado em questão ser igual teria que ser alguma de , não necessariamente múltiplo. Sendo assim a resposta é nenhuma das alternativas.
Resposta
é múltiplo de
Nenhuma das alternativas
Exercício Resolvido #6
IME – Unicamp, Aula de subespaços gerados - Adaptado
Prove que o conjunto gera .
Passo 1
Antes de tudo, pelas condições de , temos que um vetor dele pode ser escrito como
Beleza, agora temos que provar que qualquer vetor de é múltiplo do vetor de
Pelo vetor genérico de , temos que mostrar que ele pode ser escrito assim:
Passo 2
Igualando as coordenadas, temos:
Se substituirmos na equação de baixo, teremos , o que é verdadeiro né? Hahaha então de fato, qualquer vetor de pode ser escrito como múltiplo do vetor de .
Isso também pode ser visto por lógica, porque olha: todo vetor de é do formato , com a segunda coordenada sendo o dobro da primeira, assim como o vetor de .
Então se tivermos por exemplo o vetor , ele pode ser escrito como
Tendeu? :)
Resposta
Demonstração.
Exercício Resolvido #7
IME – Unicamp, Aula de subespaços gerados - Adaptado
Prove que o conjunto gera o espaço vetorial .
Passo 1
Para provarmos que o espaço é gerado por , temos que mostrar que qualquer vetor do pode ser escrito como combinação linear dos vetores de beleza?
Ou seja, supondo um vetor genérico de . Ele pode ser escrito assim:
Que é a mesma coisa que
Passo 2
Igualando as coordenadas, temos:
Substituindo na equação de cima:
Ou seja, essa igualdade é totalmente possível hehe pra que um vetor de seja escrito como combinação linear dos vetores de , basta que e .
Por exemplo, se quisermos escrever o vetor , basta que e , assim:
Resposta
Demonstração.
Exercício Resolvido #8
IME – Unicamp, Aula de subespaços gerados - Adaptado
Determine um espaço de geradores do para , dado:
Passo 1
As condições para que um vetor de pertença a são:
Substituindo a equação de baixo pela soma das duas equações e a de cima pela subtração (isso vai sumir algumas variáveis e facilitar nossa vida hehe):
O enunciado quer um espaço de geradores do , ou seja, um espaço com 2 vetores, então, entre , , e teremos duas variáveis fixas e duas livres beleza?
Passo 2
Isolando na equação de cima (você pode isolar as variáveis que você quiser)
Isolando na equação de baixo:
Passo 3
Então um vetor de pode ser escrito assim:
Boa, temos duas variáveis fixas e duas livres, igual queríamos.
Vamos separar os dos para encontrarmos os geradores:
Tirando pra fora o e :
Então, é um conjunto gerador para .
Obs: se lá no passo 2 você resolver isolar outras variáveis, sua resposta pode dar diferente, isso porque um espaço não possui apenas um conjunto gerador, ele possui vários, então não se preocupa que não necessariamente sua resposta ta errada se estiver diferente :)
Resposta
(um dos geradores possíveis, tendo e como variáveis dependentes)