Equações Cartesianas e Paramétricas
Produzido por Bruno PestanaTeoria
A Parametrização nada mais é do que um outro jeito de escrever equações, como planos e retas! Bora entender melhor como isso funciona?!
Equação Paramétrica da Reta
A equação paramétrica da reta tem essa carinha aqui:

Na figura acima temos um exemplo de uma reta
- O Ponto serve para deslocar a reta da origem;
- O vetor diretor dá a direção da nossa reta
- O parâmetro
é um número real e ele é responsável por gerar a reta!
-Mas como assim o parâmetro gera a reta?! 😖
É porque temos os pontos da nossa reta a medida que vamos mudando o parâmetro. Saca só:
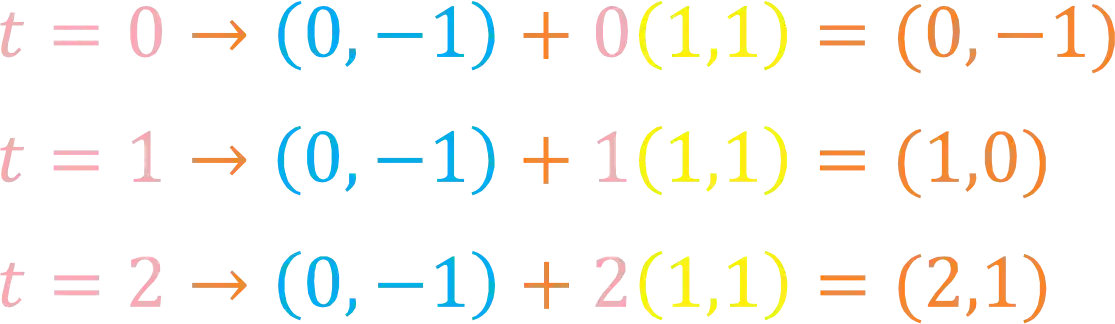
E assim temos a nossa reta:
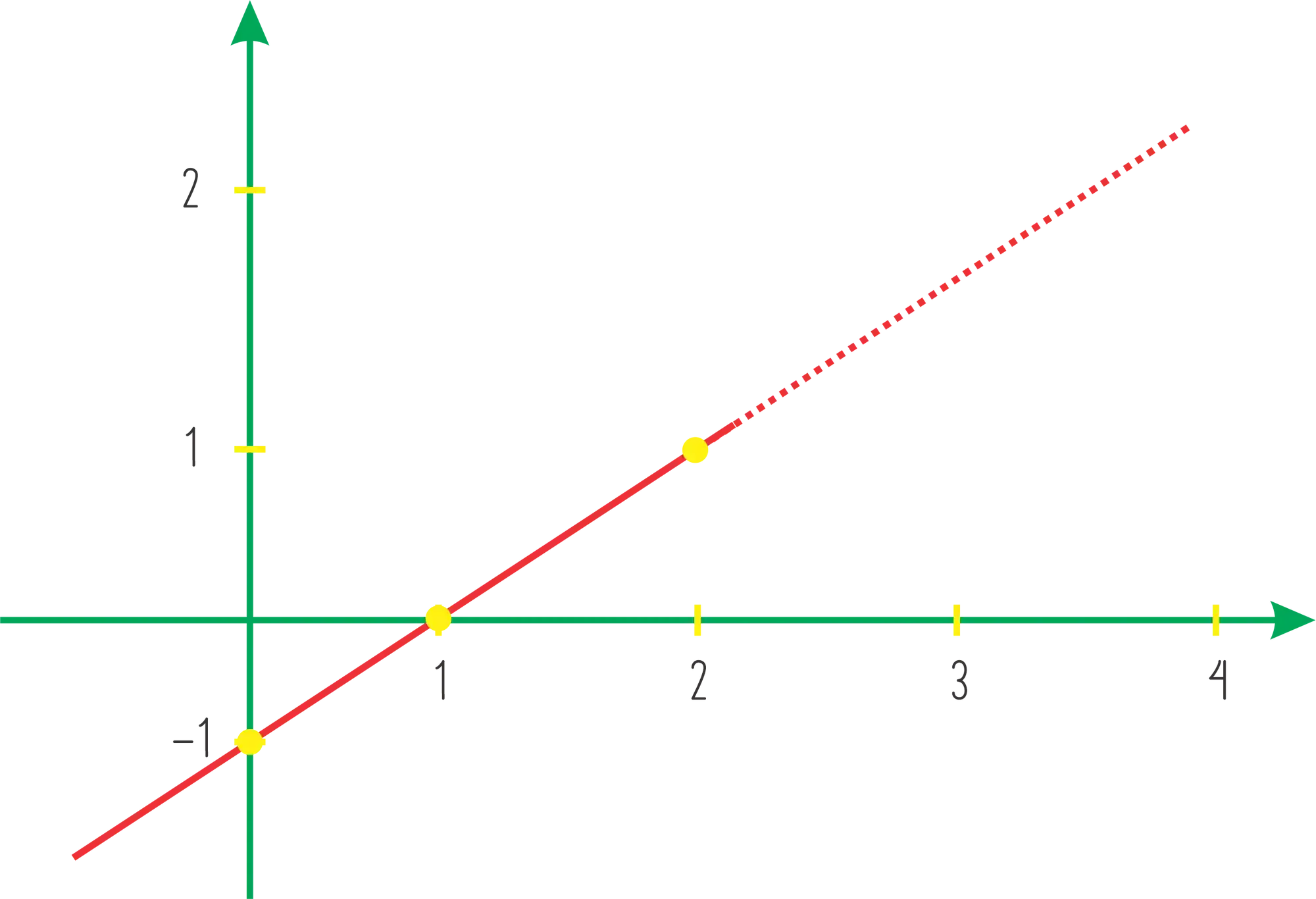
📢 Clique para ver mais:
Agora que a gente sabe o que é parametrização, bora ver como parametrizar! Pra começar com tudo, se liga nesse vídeo que o Responde Aí preparou pra você! 🧡
Como Parametrizar uma Reta?
Bora aprender na prática com um exemplo?! Vamos determinar a parametrização da reta em
Qualquer reta parametrizada, independente de estar no
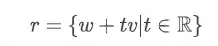
Onde
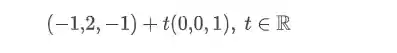
Parametrização de um Plano
Um plano é formado pelo ponto
Agora vamos ver como parametrizar um plano! Primeiro calculamos os vetores diretores:
Repara que eu subtraí do mesmo vetor? É que assim eu estou garantindo que ambos estão saindo da mesma origem. Então o nosso vetor deslocamento
Parametrização a partir de vetores e pontos
Vamos parametrizar o plano que passa pelos pontos
Parametrização a partir de equações cartesianas
Vamos considerar a seguinte equação referente a um plano no
Para passar ela para sua forma paramétrica, primeiro isolamos as variáveis:
Agora vamos substituir num vetor genérico do espaço, no caso o
Os nossos parâmetros serão y e z, logo:
Ou seja, a parametrização para o plano é:
Agora vamos praticar com exercícios?
Como Parametrizar uma Reta?
Parametrização de um Plano
Exercícios Resolvidos
Exercício Resolvido #1
Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 23 – Prob. 1.7
Determine a parametrização para o plano (em ):
Determine uma parametrização para as retas (em )
Passo 1
Letra
Como temos uma equação, vamos ter que isolar alguma variável, no caso, irei isolar o :
Passo 2
Letra
Para começar devemos resolver o sistema achando as soluções:
Assim a parametrização é:
Letra
Repetindo os mesmos passos da letra :
Ihhh, então só vai dar um ponto?? Não!!!! Não se esqueça do que não apareceu no sistema:
Assim a parametrização é:
Resposta
Exercício Resolvido #2
Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 23 – Prob. 1.5
Determine a parametrização para a reta (em ):
Que contém o ponto e é paralela ao vetor
Que pertence ao plano e ao plano
Determine uma parametrização para o plano (em ) que contém o(s) ponto(s):
e é simultaneamente paralelo aos vetores e
e a reta parametrizada por
Passo 1
Letra
Como nós já temos o vetor e o ponto por onde a reta passa, basta montar a parametrização:
Letra
Como pertencem aos dois planos, basta resolver o sistema com as duas equações cartesianas (ou seja, vamos achar a interseção dos dois planos):
E assim a equação paramétrica é:
Passo 2
Letra
Como temos os pontos, basta definirmos os vetores diretores, com uma origem para os mesmos vetores:
Assim nossa parametrização será:
Letra
Como já temos os vetores e o ponto, basta montar a parametrização:
Passo 3
Letra
Podemos ver que a parametrização da reta é:
Sendo assim, vemos que é uma reta deslocada da origem. Como ela já tem um vetor diretor, para formar um plano basta achar o segundo. Podemos interpretar o problema agora como um plano que passa pelos pontos e paralelo ao vetor :
Sendo assim, vamos achar o segundo vetor diretor:
Assim nossa parametrização fica:
Resposta
Exercício Resolvido #3
Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 23 – Prob. 1.3
Determine equações cartesianas para retas (em ):
Determine equações cartesianas para as retas (em ):
Passo 1
Letra
Bom, o sistema já está montado em todas as letras, então só precisamos isolar os parâmetros.
A equação cartesiana é
Letra
A equação cartesiana é
Passo 2
Em todas as letras só é necessário isolar os parâmetros e resolver o sistema, logo vamos fazer isso.
Letra
As equações cartesianas são:
Letra
Como não conseguimos substituir o parâmetro , pode assumir qualquer valor e, portanto as equações cartesianas são:
Resposta
Exercício Resolvido #4
Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 23 – Prob. 1.8
Determine equações cartesianas para os planos (em ):
Passo 1
Letra a)
Isolando os parâmetros e substituindo nas outras equações:
Assim, a equação cartesiana é:
Letra b)
Isolando os parâmetros e substituindo nas outras equações:
Como não conseguimos substituir e nem , e podem assumir quaisquer valores e, portanto, a equação cartesiana é:
Passo 2
Letra c)
Isolando os parâmetros e substituindo nas outras equações:
Assim, a equação cartesiana é:
Letra d)
Isolando os parâmetros e substituindo nas outras equações:
Como não conseguimos substituir , pode assumir qualquer valor e, portanto, a equação cartesiana é:
Resposta
Exercício Resolvido #5
Elaboração própria.
Considere as afirmativas a seguir:
I – O espaço representa uma reta.
II – O espaço representa um plano.
III – A parametrização da reta pode ser dada por
Estão corretas apenas as afirmativas:
a) I
b) II
c) III
d) I e II
e) I e III
f) II e III
g) I, II e III
Passo 1
Bora analisar as afirmativas:
I – Verdadeira. Lembra que a gente viu que quando tem apenas um vetor com parâmetro (no caso, ) é porque se trata de uma reta? :D
II – Vamos tomar cuidado com esse caso. A gente tem 2 vetores parametrizados, beleza, vimos que isso se trata de um plano então. Opa! Mas os 2 vetores são múltiplos, repara que o segundo vetor é 3 vezes o primeiro. Então poderíamos escrever esse espaço assim
Ou seja, se trata de apenas um vetor hehe então é uma reta e a afirmativa é falsa!
III – Vamos parametrizar essa reta. O já está isolado, então vamos igualar a um vetor genérico:
Trocando por :
Obaa, então a afirmativa está certa :D
Então a alternativa correta é a letra E ;)
Resposta
e) I e III
Exercício Resolvido #6
Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª ed., Rio de Janeiro, Instituto de Matemática, 2012 – Adaptado.
Considere a reta .
Verifique se .
Passo 1
Antes de ver se um ponto pertence a uma reta, temos que achar o ponto genérico dessa reta, pra isso, primeiro vamos multiplicar o vetor parametrizado por :
Agora é só somar:
Passo 2
Ok, tendo o ponto genérico, vamos igualar a e ver se existe um que satisfaça nossa condição:
Igualando as coordenadas:
Passo 3
Isolando na equação :
Agora, isolando na equação
Opa, em cada equação obtivemos um valor diferente para o parâmetro , isso significa que não existe um que faça a reta passar por , e logo, esse ponto não pertence à reta :/
Resposta
Não pertence.
Exercício Resolvido #7
Elaboração própria.
Dada a reta , dê sua equação paramétrica (com parâmetro ) e determine o que leva a reta aos seguintes pontos:
a) ponto )
b) origem
Passo 1
Antes de tudo, vamos parametrizar a reta beleza?
Somando as duas equações:
Humm, vamos isolar o pode ser? Mas se você quiser pode isolar o ou o também hehe
Da segunda equação, temos que , vamos substituir isso na equação acima:
Passo 2
Beleza, agora chegou a hora de igualar a um vetor genérico. Temos que
(repare que escrevemos e em função de para igualarmos. Isso significa que será o nosso parâmetro).
Separando os em um vetor e os números em outro:
Agora vamos tirar o pra fora:
Transformando em um parâmetro , como pede o enunciado:
Aeee, parametrizamos nossa reta :D Agora vamos pros próximos passos!
Passo 3
a) Queremos saber em qual valor do parâmetro a nossa reta vai passar pelo ponto certo? Primeiro, vamos achar um ponto genérico da nossa reta, pra isso, temos que primeiro multiplicar o vetor parametrizado pelo parâmetro, assim:
Agora, vamos somar tudo. Assim, um ponto genérico da nossa reta (ou seja, qualquer ponto dela pode ser escrito assim para diferentes valores de ) é:
Agora bora igualar esse ponto genérico ao ponto que queremos:
Igualando cada coordenada, temos:
Em , temos que . Mas precisamos substituir isso em e também para termos certeza que esse ponto existe na reta:
Boaaa, procede pras duas equações, logo, realmente com temos o ponto desejado :D
Passo 4
b) Aqui, o esquema é o mesmo do passo anterior, vamos igualar o ponto genérico à origem, ou seja, :
Igualando as primeiras coordenadas, temos que .
Mas se igualarmos as segundas e as terceiras coordenadas e então substituirmos , teremos
Poxa, então a origem não pertence à reta, pois não existe um tal que o ponto genérico da reta se iguale a :/
Resposta
a)
b) A reta não passa pela origem.
Exercício Resolvido #8
Elaboração própria.
Dado o plano , dê sua equação paramétrica (com parâmetros e ) e determine o e o que levam o plano ao ponto .
Passo 1
Vamos parametrizar esse plano.
Isolando o (já que o enunciado fala que e serão nossos parâmetros)
Agora vamos igualar a :
(repara que como se trata de um plano, temos 2 parâmetros: e )
Separando , e os números:
Tirando os parâmetros pra fora:
Agora vamos transformar em parâmetros: e
E temos nossa equação parametrizada :)
Passo 2
Beleza, agora queremos encontrar o e o que fazem o plano passar pelo ponto . Antes, vamos encontrar um ponto genérico do plano:
Passo 3
Boa, agora é só igualar com o ponto desejado:
Igualando as coordenadas:
Passo 4
Das equações e já temos os valores de e , agora vamos substituí-los na equação e ver se procede para todas as coordenadas:
Aeee, isso significa que o ponto realmente pertence a esse plano e que o plano passa por ele quando e ;)
Resposta
e