Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Distância entre Ponto e Plano

Ver Todos os Exercícios

Teoria

Já pode até comemorar que o capítulo tá quaseee acabando!!

Vamos começar logo então! Entender a distância entre um ponto e um plano!

Se tivermos um ponto P = ( x 0 ,   y 0 ,   z 0 ) e um plano π com equação geral:

a x + b y + c z + d = 0

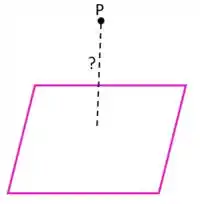
Se observamos bem, existem várias possíveis distâncias entre o ponto p e p plano π , por exemplo:

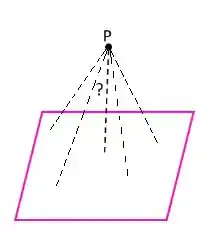
Beleza?!

A distância entre o ponto P e o plano π , será sempre a menor distância possível! E para isso acontecer, teremos que pegar a distância que ficará perpendicular ao plano usando o vetor normal:

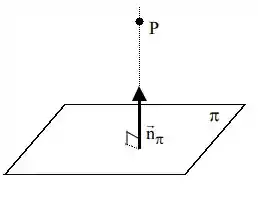
Suponha um plano π com equação geral: a x + b y + c z + d = 0 e um ponto P = ( x 0 ,   y 0 ,   z 0 ) , A distância entre o ponto e o plano é:

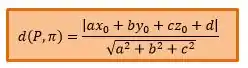
E é só essa formulinha aí!

Para fechar, vamos fazer um exemplo!

Considere o plano π : 2 x + y - z + 5 = 0 e o ponto P = ( 3 ,   2 ,   1 ) . Qual é a distância entre eles??

Bom, galera é só aplicar a fórmula! Olha só:

Da equação do plano, temos a = 2 ,   b = 1 ,   c = - 1 ,   d = 5 e sabemos que P = 3 ,   2 ,   1 = ( x 0 , y 0 , z 0 ) . Agora só falta substituir na fórmula!

d P ,   π = a x 0 + b y 0 + c z 0 + d a 2 + b 2 + c 2

d P ,   π = 2 × 3 + 1 × 2 + - 1 × 1 + 5 2 2 + 1 2 + - 1 2

Logo, d P ,   π = 12 6      

Prontinho!

Nossa teoria fica por aqui! Mas não se esquece de fazer os exercícios para ir se acostumando com a cara das fórmulas!!

Exercícios Resolvidos

Exercício Resolvido #1

Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 224-1.

Calcule a distância do ponto P = ( 1 ,   2 ,   - 1 ) ao plano π : 3 x - 4 y - 5 z + 1 = 0 .

Passo 1

Vamos esquentar bem os motores??!!

O enunciado nos dá o ponto P = ( 1 ,   2 ,   - 1 ) e a equação geral do plano π : 3 x - 4 y - 5 z + 1 = 0 e pede para calcularmos a distância entre o ponto e o plano. Opa!! Essa é a única fórmula que decorei!! Então, bora aplicá-la!!

Passo 2

Vimos na teoria que a fórmula para calcular a distância entre ponto e plano é:

d P , π = a x 0 + b y 0 + c z 0 + d a 2 + b 2 + c 2

Sendo que x 0 ,   y 0 ,   z 0 são as coordenadas do ponto e a ,   b ,   c e d são os coeficientes da equação geral do plano. Então, temos que:

P = 1 ,   2 ,   - 1 = ( x 0 ,   y 0 ,   z 0 )

π : 3 ,   - 4 ,   - 5 ,   1 = ( a ,   b ,   c ,   d )

Passo 3

Então, agora, só falta colocar os valores na fórmula e calcular:

d P , π = a x 0 + b y 0 + c z 0 + d a 2 + b 2 + c 2 = 3.1 + - 4 . 2 + - 5 . - 1 + 1 3 2 + ( - 4 ) 2 + ( - 5 ) 2

Resolvendo:

d P , π = 3 - 8 + 5 + 1 50 = 1 5 2 = 2 10

Pronto!! Chegamos na solução:

d P , π = 2 10

Resposta

d P , π = 2 10

Exercício Resolvido #2

Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 198-5.

Calcular a distância do ponto P 0 = ( - 4 ,   2 ,   5 ) ao plano π : 2 x + y + 2 z + 8 = 0 .

Passo 1

Belezoca, o moço já deu para gente o vetor normal do plano e o plano! Agora é só jogar esses valores da formulinha marota e partir para o abraço!

Vamos lá!

Passo 2

O nosso vetor normal é   n → = ( 2,1 ,   2 ) e d = 8 , o ponto é P 0 = ( - 4 ,   2 ,   5 ) . Vamos substituir esses valores na fórmula aí de baixo

d P , π = a x 0 + b y 0 + c z 0 + d a 2 + b 2 + c 2

Ficaremos com:

d P , π = 2 × ( - 4 ) + 1 × 2 + 2 × 5 + 8 2 2 + 1 2 + 2 2

d P , π = 12 9 = 12 3 = 4   u . c

Resposta

d P , π = 4   u . c

Exercício Resolvido #3

Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 202-6.

Determinar a distância do ponto P = ( 2 ,   - 1 ,   2 ) a cada um dos planos:

  1. π : 2 x - 2 y - z + 3 = 0
  2. π : x + y + z = 0
  3. π : 2 x + y = 3

Passo 1

Mais uma vez usaremos nossa formulinha marota:

d P , π = a x 0 + b y 0 + c z 0 + d a 2 + b 2 + c 2

Começando pela letra a, temos que   n → = ( 2 ,   - 2 ,   - 1 ) e d = 3 . Também sabemos que que

P = 2 ,   - 1 ,   2 .

Colocando na fórmula,

d P , π = 2 × 2 + ( - 2 ) × ( - 1 ) + ( - 1 ) × 2 + 3 2 2 + ( - 2 ) 2 + ( - 1 ) 2 = 7 3   u . c

Passo 2

Vamos fazer a letra b agora!

O nosso vetor normal é   n → = ( 1 , 1 ,   1 ) e d = 0 , o ponto é o mesmo. Vamos substituir esses valores na fórmula aí de baixo

Ficaremos com:

d P , π = 1 × 2 + 1 × ( - 1 ) + 1 × 2 + 0 1 2 + 1 2 + 1 2

d P , π = 3 3 = 3   u . c

Passo 3

Falto só a letra c! Bora terminar esse exercício!!

n → = ( 2 ,   1 ,   0 ) e d = - 3 , o ponto continua o mesmíssimo.

A “formulosa” fica assim ô:

d P , π = 2 × 2 + 1 × ( - 1 ) + 0 × 2 + ( - 3 ) 2 2 + 1 2 + 0 2 = 0

Resposta

  1. 7 3 u . c
  2. 3 u . c
  3. 0

Exercício Resolvido #4

Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 202-7.

Achar a distância do ponto P = ( 2 ,   - 3 ,   5 ) ao plano π : 3 x + 2 y + 6 z - 2 = 0

Passo 1

Outra vez, usaremos a “formulosa”:

d P , π = a x 0 + b y 0 + c z 0 + d a 2 + b 2 + c 2

Você já deve estar careca de saber essa fórmula!

Nesse problema temos que   n → = ( 3 ,   2 ,   6 ) e d = - 2 . Também sabemos que que

P = 2 ,   - 3 ,   5 .

Colocando na fórmula,

d P , π = 3 × 2 + 2 × - 3 + 6 × 5 - 2 3 2 + 2 2 + 6 2 = 28 49  

d P , π = 4   u . c

Resposta

d P , π = 4   u . c

Exercício Resolvido #5

Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 202-8.

Achar a distância da origem a cada um dos planos

  1. π : 3 x - 4 y + 20 = 0

  2. π : x = 2 - h + 2 t y = 1 + 3 h - t z = - t

Passo 1

Como de praxe, vamos começar pela letra a.

Mais uma vez, usaremos a “formulosa”:

d P , π = a x 0 + b y 0 + c z 0 + d a 2 + b 2 + c 2

Mas agora  n → = ( 3 ,   - 4 ,   0 ) e d = 20 . Como o moço quer a distância até a origem, P = 0 ,   0 ,   0 .

Colocando na fórmula,

d P , π = 3 × 0 + - 4 × 0 + 0 × 0 + 20 3 2 + ( - 4 ) 2 + 0 2 = 20 25  

d P , π = 4   u . c

Passo 2

Agorinha, vamos fazer a letra b!

O nosso amigo quis complicar nossa vida e nos deu a equação paramétrica do plano, vamos ter que passar para a equação geral! Isso significa que precisamos achar um vetor normal ao plano e um ponto desse plano. A equação paramétrica dá para gente dois vetores paralelos (ao plano), sendo eles:

u → = - 1 ,   3 ,   0

v → = ( 2 ,   - 1 ,   - 1 )

Se nós buscamos o vetor normal, que é perpendicular ao plano e consequentemente perpendicular a   u → e   v → , é só fazer o produto vetorial   u → × v → que acharemos   n → !!

Obs: Se você deu aquela esquecida básica em vetores, o produto vetorial dá para gente um vetor perpendicular aos dois vetores que geraram ele. No nosso caso, vai gerar um vetor perpendicular a   u → e   v → , que é exatamente   n → 😉

Voltando a vaca fria...

Vamos fazer o produto vetorial!

u → × v → = i → j → k → - 1 3 0 2 - 1 - 1 = ( - 3 ,   - 1 ,   - 5 )

Show de bolinhas, já temos   n → = ( - 3 ,   - 1 ,   - 5 ) ! Vamos substituir na fórmula geral:

a x + b y + c z + d = 0

- 3 x - 1 y - 5 z + d = 0

Epa, quem é d ??

Calma, galeris! Para achar d é só substituir um ponto do plano. Olhando para a equação paramétrica achamos P p l a n o = ( 2 ,   1 ,   0 ) , logo

- 3 × 2 - 1 × 1 - 5 × 0 + d = 0 → d = 7

Passo 3

Agora sim podemos substituir tudo na fórmula e achar a bendita distância!

Se você é meio Dori e tem perda de memória recente (haha), a fórmula para distância entre ponto e plano é:

d P , π = a x 0 + b y 0 + c z 0 + d a 2 + b 2 + c 2

Sendo, nesse caso,   n → = ( - 3 ,   - 1 ,   - 5 ) e d = 7 . O ponto é a origem, logo P = 0,0 , 0 . Substituindo na fórmula:

d P , π = - 3 × 0 + - 1 × 0 + ( - 5 ) × 0 + 7 ( - 3 ) 2 + ( - 1 ) 2 + ( - 5 ) 2 = 7 35 u . c

Resposta

  1. d P , π = 4   u . c
  2. d P ,   π = 7 35 u . c

Exercício Resolvido #6

Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 234-20.

Dê uma equação geral do plano π que contém a reta r : X = 1 ,   0 ,   1 + λ ( 1 ,   1 ,   - 1 ) e dista 2 do ponto P = ( 1 ,   1 ,   - 1 )

Passo 1

Precisamos encontrar a equação geral do plano π . Para isso, precisamos encontrar o vetor normal ao plano e um ponto que pertence à ele. O ponto nós já temos, pois o enunciado nos diz que a reta r está contida no plano, então o ponto ( 1 ,   0 ,   1 ) pertence à π . Falta, acharmos o vetor normal n → = ( a ,   b ,   c ) . Para isso, temos duas informações: de que o plano dista 2   do ponto ( 1 ,   1 ,   - 1 ) e como r está contida no plano, isso significa que eles são paralelos também

Passo 2

Começando pelo paralelismo, sabemos que reta e plano são paralelos se:

a e + b f + c g = 0

Sendo a ,   b ,   c incógnitas e e ,   f ,   g = ( 1 ,   1 ,   - 1 ) que são as coordenadas do vetor diretor de r , então:

a + b - c = 0 →   c = a + b

Temos uma primeira relação.

Se sabemos que a equação geral de um plano é a x + b y + c z + d = 0 e temos um ponto que pertence ao plano ( 1 ,   0 ,   1 ) , conseguimos achar d :

a + c + d = 0 → d = - a - c

Temos uma segunda relação. E substituindo a primeira na segunda, temos:

Beleza?!

Passo 3

A terceira obteremos fazendo a distância entre o ponto ( 1 ,   1 ,   - 1 ) e ( a ,   b ,   c , d ) que sabemos que vale 2 . Agora, sim, vamos colocar na fórmula:

d P , π = a x 0 + b y 0 + c z 0 + d a 2 + b 2 + c 2

2 = a + b - c + d a 2 + b 2 + c 2

Substituindo a relação d = - 2 a - b e c = a + b , temos:

2 = a + b - c + d a 2 + b 2 + c 2 → 2 = a + b - a - b - 2 a - b a 2 + b 2 + ( a + b ) 2

Resolvendo:

2 = - 2 a - b 2 a 2 + 2 b 2 + 2 a b

Elevando ao quadrado:

2 .   2 a 2 + 2 b 2 + 2 a b = ( - 2 a - b ) 2

4 a 2 + 4 b 2 + 4 a b = 4 a 2 + 2 b 2 + 4 a b

Se b = 0 , então:

c = a

d = - 2 a

Assim, os coeficientes da equação geral do plano são:

a ,   0 ,   a ,   - 2 a = ( a ,   b ,   c ,   d )

Então, a equação do plano é:

S e   a = 1

x + z - 2 = 0

Resposta

x + z - 2 = 0

Exercícios de Livros Relacionados

Mostre que a distância entre os planos paralelos a x + b y + c z + d 1 = 0 e a x + b y + c z + d 2 = 0 é D = | d 1 - d 2 | a 2 + b ² + c ² ² ²
Determine a distância entre os planos paralelos dados. z = x + 2 y + 1 ;3 x + 6 y - 3 z = 4
Determine a distância entre os planos paralelos dados. 3 x + 6 y - 9 z = 4 , x + 2 y - 3 z = 1
Determine as equações dos planos que são paralelos ao plano x + 2 y - 2 z = 1 e que distam duas unidades dele.
Determine a distância do ponto ao plano dado.(3 , - 2,7) , 4 x - 6 y + z = 5