Exercícios de Distância entre Ponto e Plano - Lista de Exercícios Resolvida

Calcule a distância do ponto ao plano .

Calcular a distância do ponto ao plano

Achar a distância do ponto ao plano

Dê uma equação geral do plano que contém a reta e dista do ponto

Achar a distância da origem a cada um dos planos

Determinar a distância do ponto a cada um dos planos:

Assuma orientado e considere coordenadas de pontos dadas em relação a um sistema de coordenadas fixado em de base ortonormal e positiva.

A distância entre o ponto e o plano

É

a)

b)

c)

d)

e)

f)

Assuma orientado e considere coordenadas de pontos dadas em relação a um sistema de coordenadas fixado em de base ortonormal e positiva.

Seja . A distância entre o ponto e o plano é menor ou igual a se, e somente se, pertence ao intervalo

a)

b)

c)

d)

e)

Considere um sistema de coordenadas em , em que é uma base ortonormal de . Seja a reta dada pela equação

e seja um plano que contenha a reta e diste da origem . Sejam e suponha que o vetor seja normal ao plano . Temos que é igual a:

1. ;
2. ;
3. ;
4. ;
5. .

Considere o ponto de , a reta de equações paramétricas

E o plano de equação cartesiana

1. Calcule a distância do ponto ao plano e as coordenadas do ponto do plano mais próximo de .
2. Determine a equação cartesiana do plano que contém o ponto e a reta .
3. Considere o ponto e o plano de de equação cartesiana

Observe que . Determine uma equação paramétrica da reta contida no plano que contém e é perpendicular a .

4. Considere a reta de equações paramétricas

Determine para que as retas e se interceptem em um ponto.

Considere os pontos , e a reta

Seja um plano tal que , a reta não intersecte e o ponto não pertença a . Se são tais que uma equação geral para é

Então é igual a

;

Considere o octaedro regular (isto é, cujas faces são triângulos equiláteros) de vértices , conforme a figura

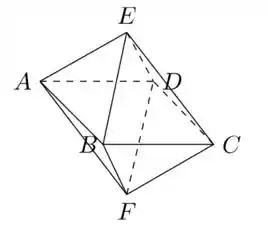
Sabendo que e que a segunda coordenada de é positiva, se é o plano que contém os pontos e é o ponto de mais próximo de , então é igual a

a) 6

b) 2

c) 5

d) 4

e) 3

Considere o plano de equação e os pontos ) e

(a) Encontre uma equação paramétrica para a reta que passa pelos pontos e .

(b) Calcule a distância entre o plano e o ponto .

(c) Encontre a equação cartesiana do plano que contém os pontos e e é ortogonal ao plano .

Considere a reta e o plano .

a) Determine a equação geral do plano .

b) Determine o ponto , intersecção do plano com a reta .

c) Determine o ponto correspondente a e calcule a distância de ao plano .

São dados as retas e o plano e o ponto

a) Determine a posição relativa entre e .

b) Determine a projeção do ponto sobre a reta .

c) Determine a projeção do ponto sobre o plano .

d) Determine o ângulo entre a reta e a reta .

Considere o plano e as retas concorrentes

Se é o ponto na interseção de e , então a distância de ao plano é igual a:

A distância do ponto ao plano

É igual a:

Seja o ponto simétrico de em relação ao plano

Então é igual a:

Considere o ponto e o plano , definido por

Então, a distância do ponto ao plano é igual a

a)

b)

c)

d)

e)

Sejam pontos de que não estão em um mesmo plano e seja o ponto do segmento tal que Se são números reais tais que então o produto vale:

a)

b)

c)

d)

e)

Considere os pontos

e ,

a reta de equações paramétricas

e o plano suja equação cartesiana é

Considere o ponto

d) Determine a distância do ponto ao plano e um ponto de tal que a distância entre e seja .