Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Combinação Linear

Ver Todos os Exercícios

Teoria

Quer aprender Combinação Linear? Então vem com o Responde Aí!

O que é uma Combinação Linear de Vetores?

Combinação linear é a representação de um vetor a partir de operações com outros vetores!

-Como assim?! 😖

Pra entendermos melhor a ideia de combinação linear de vetores vamos olhar um exemplinho! Olha esse vetor aqui: .

Podemos reescrever ele de um outro jeito:

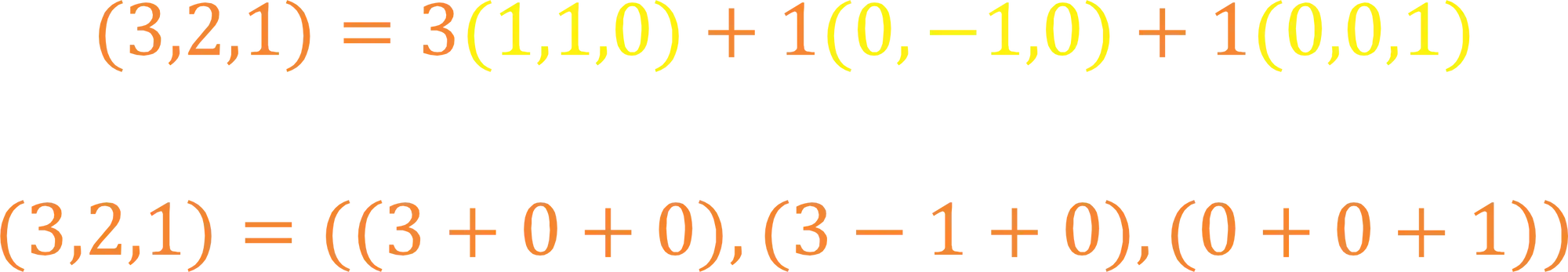
Combinação Linear de Vetores
Combinação Linear de Vetores

Irado, não é?

Note que o vetor pode ser escrito como uma soma dos vetores , e , multiplicados por um escalar.

Nesse caso, podemos dizer que o vetor é uma COMBINAÇÃO LINEAR (CL) do conjunto de vetores .

Podemos definir formalmente como na imagem abaixo:

Definição formal de combinação linear
Definição formal de combinação linear

Normalmente, as questões dizem que um vetor é uma combinação linear de outros e querem saber quais os coeficientes que tornam a afirmação verdadeira ou perguntam se um vetor é combinação linear de outros. Em qualquer alternativa, temos que calcular os coeficientes.

📢Clique para saber mais:

Como descobrir a Combinação Linear de Vetores

Parece complicado, mas não é! Vamos fazer um exemplo aqui:

O vetor  é uma combinação linear de ?

Você pode conferir a resolução desse exemplo, nesse vídeo iradoso que o e Responde Aí preparou especialmente pra você! 🧡 👇

Ou então continua comigo no textinho!

Vamos tentar achar  e  que satisfaçam a equação:

Vamos multiplicar os vetores pelos coeficientes e somar as coordenadas correspondentes:

Agora, podemos montar um sistema igualando as coordenadas correspondentes:

De cara, . Mas ao substituir isso nas duas outras equações temos que  e . Pode  assumir dois valores distintos? Não pode! Temos uma CONTRADIÇÃO!! UM ABSURDO!!

Um absurdo desses significa que não dá para escrever o vetor como proposto, ou seja, o vetor  NÃO É CL de !

Se fosse possível, encontraríamos coeficientes condizentes. Sacou? Agora você já está pronto para praticar bastante com os nossos exercícios resolvidos passo a passo!

Exercício: Determine o valor de k para que o vetor u=(0,2,1,k) seja combinação linear do conjunto de vetores {(1,0,1,3),(2,1,2,0),(0,3,1,0)}

A resolução desse problema você encontra nesse vídeo aqui!

Agora vamos praticar com mais exercícios?!

Exercício: Determine o valor de k para que o vetor u=(0,2,1,k) seja combinação linear do conjunto de vetores {(1,0,1,3),(2,1,2,0),(0,3,1,0)}

Exercícios Resolvidos

Exercício Resolvido #1

Alfredo Steinbruch e Paulo Winterle, Álgebra Linear, 2ª ed., São Paulo, Pearson, 1987, pp. 90. - 27

Sejam os vetores u = ( 2 , - 3,2 ) e v = ( - 1 ,   2,4 ) em R 3

a   Escreva o vetor w = ( 7 , - 11,2 ) como combinação linear de u e v

b   Para que valor de k o vetor ( - 8,14 , k ) é combinação linear de u e v ?

c   Determinar uma condição entre a , b e c para que o vetor ( a , b , c ) seja uma combinação linear de u e v .

Passo 1

Letra ( a )

Para escrever o vetor w como C L de u , v queremos o seguinte:

w = a u + b v

Ou seja, temos que achar os coeficientes de u , v que satisfazem essa equação:

w = a u + b v

Podemos montar um sistema com os coeficientes

Vamos isolar a na I I I :

2 = 2 a + 4 b

1 = a + 2 b

a = 1 - 2 b

Agora substituímos em ( I ) :

7 = 2 1 - 2 b - b

7 = 2 - 4 b - b

5 = - 5 b

b = - 1

E por fim substituímos o valor de b para encontrar a I I I :

2 = 2 a + 4 b

1 = a + 2 b

a = 1 - 2 b

a = 1 - 2 - 1 = 3

a = 3

Passo 2

Muita calma agora! Se o sistema só tivesse as equações ( I ) e ( I I I ) estaria sussa e poderíamos terminar por aqui. Entretanto, jovem padawan, temos que ver se os resultados achados satisfazem a outra equação não usada, no caso a ( I I ) :

- 11 = - 3 3 + 2 - 1

- 11 = - 9 - 2 = - 11 ⇒ 7 , - 11,2 = a 2 , - 3,2 + b - 1,2 , 4

- 11 = - 11

Ufa! Deu tudo certo! Então a nossa combinação fica assim:

w = 3 u - v

Não se esqueça de sempre conferir isso ;)

Passo 3

Letra ( b )

Mesma coisa que a letra ( a )

Na primeira equação podemos isolar o b :

- 8 = 2 a - b

b = 2 a + 8

E substituir na segunda equação:

14 = - 3 a + 2 b

3 a = 2 b - 14

3 a = 2 ( 2 a + 8 ) - 14

a = - 2

E por fim podemos encontrar o valor de b :

b = 2 a + 8

b = 2 ( - 2 ) + 8

b = 4

Bom, percebe que temos 3 equações? Então, com as duas primeiras já dá pra achar a , b . Mas e a terceira serve pra que??? Bom a gente pega os valores de a , b e substitui para achar k :D:

Encontrando k :

k = 2 - 2 + 4 ⋅ 4 ⇒

k = 12

Passo 4

Letra ( c )

Para determinar um condição precisamos montar uma C L com o vetor ( a , b , c ) . Desta vez vou chamar os coeficientes de u , v de k 1 ,   k 2 respectivamente.

a , b , c = k 1 2 , - 3,2 + k 2 - 1,2 , 4

Vamos montar o sistema:

Vamos primeiro isolar o k 2 na primeira equação:

a = 2 k 1 - k 2

k 2 = 2 k 1 - a

E substituir na segunda equação para encontrar k 1 em função de a   e   b :

Podemos voltar na primeira equação e encontrar o valor de k 2 substituindo o valor de k 1 :

E por fim , substituir os valores de k 1 e k 2 na terceira equação para encontrar o valor de c em função de a   e   b :

Em outras palavras, o que resolvi aí em cima, foi achar os coeficientes k 1 ,   k 2 que satisfaçam a combinação linear que estipulamos. Como consequência desses resultados, conseguimos achar uma relação entre a , b , c necessária para existir a combinação linear.

Resposta

a   w = 3 u - v

b   k = 12

c   c = 16 a + 10 b

Exercício Resolvido #2

Elaboração própria

Verificar se o vetor u = ( 4 , - 4,1 , 3 ) é combinação linear do conjunto de vetores - 1 ,   - 2 ,   0 ,   3 ,   2 ,   - 1 ,   0 ,   0 ,   ( 1 ,   0 ,   1 ,   0 )

Passo 1

Beleza, para ver se u é C L desse conjunto, vamos escrever o sisteminha:

( 4 ,   - 4 ,   1 ,   3 ) = a - 1 ,   - 2 ,   0 ,   3 + b 2 ,   - 1 ,   0 ,   0 + c ( 1 ,   0 ,   1 ,   0 )

Abrindo isso:

4 = - 1 a + 2 b + 1 c     ( I ) - 4 = - 2 a + - 1 b     ( I I ) 1 = 1 c     ( I I I ) 3 = 3 a       ( I V )

De ( I I I ) tiramos que c = 1 .

De ( I V ) tiramos que a = 1 .

Substituindo isso em ( I I ) :

- 4 = - 2 × 1 - b

b = 2

Vamos só substituir nossos valores em ( I ) e ver se bate!

4 = - 1 × 1 + 2 × 2 + 1 × 1

4 = 4 → O K !

Logo, nossa C L será

u = - 1 ,   - 2 ,   0 ,   3 + 2 2 ,   - 1 ,   0 ,   0 + ( 1 ,   0 ,   1 ,   0 )

Resposta

u = - 1 ,   - 2 ,   0 ,   3 + 2 2 ,   - 1 ,   0 ,   0 + ( 1 ,   0 ,   1 ,   0 )

Exercício Resolvido #3

Elaboração própria

Determine o valor de k para que o vetor u = ( 0 ,   2 ,   1 ,   k ) seja combinação linear do conjunto de vetores 1 ,   0 ,   1 ,   3 ,   2 ,   1 ,   2 ,   0 ,   ( 0 ,   3 ,   1 ,   0 )

Passo 1

Mais uma vez partimos para o sistema:

( 0 ,   2 ,   1 ,   k ) = a 1 ,   0 ,   1 ,   3 + b 2 ,   1 ,   2 ,   0 + c ( 0 ,   3 ,   1 ,   0 )

Abrindo isso:

0 = 1 a + 2 b   ( I ) 2 = b + 3 c     ( I I ) 1 = 1 a + 2 b + 1 c     ( I I I ) k = 3 a       ( I V )

Opa! k só está em função de a , então precisamos achar a !

De ( I ) tiramos que a = - 2 b .

De ( I I ) tiramos que c = 2 - b 3 .

Substituindo isso em ( I I I ) em função de b :

1 = - 2 b + 2 b + 2 - b 3

3 = - 6 b + 6 b + 2 - b

b = - 1

Com o valor de b conseguimos achar a !

a = - 2 × - 1

a = 2

Logo,

k = 3 × 2

k = 6

Resposta

k = 6

Exercício Resolvido #4

Alfredo Steinbruch e Paulo Winterle, Álgebra linear, 2ª edição, São Paulo, Pearson, 1987, pp. 40 - Modificada

Mostrar que o vetor  v → = ( 4 ,   3 ,   - 6 ) não é combinação linear de   v 1 → = ( 1 ,   - 3 ,   2 ) e   v 2 → = ( 2 ,   4 ,   - 1 ) .

Passo 1

Ok, vamos começar tentando escrever  v → como C L de   v 1 → e   v 2 → !

Ficaria assim:

v → = a v 1 → + b v 2 →

4 ,   3 ,   - 6 = a 1 ,   - 3 ,   2 + b 2,4 ,   - 1

Abrindo em um sisteminha,

4 = 1 a + 2 b     I 3 = - 3 a + 4 b     I I - 6 = 2 a - 1 b     I I I

De ( I ) tiramos que a = 4 - 2 b   ( i ) .

Substituindo em ( I I ) ,

3 = - 3 4 - 2 b + 4 b

3 = - 12 + 6 b + 4 b

15 = 10 b

b = 15 10 = 1,5

Substituindo b = 1 ,   5 em ( i ) ,

a = 4 - 2 × 1 ,   5

a = 1

Show! Achamos a e b ! Agora precisamos ver se esses valores encontrados satisfazem a equação ( I I I ) .

Substituindo a = 1 ,   b = 1 ,   5 em ( I I I ) :

2 × 1 - 1 ,   5 =   ?

2 - 1 ,   5 = 0,5 ≠ - 6

Logo, os valores de a e b não satisfazem a equação ( I I I ) e   v → não é C L de   v 1 → e   v 2 → !

Resposta

v → não é C L de   v 1 → e   v 2 → !

Exercício Resolvido #5

Alfredo Steinbruch e Paulo Winterle, Álgebra linear, 2ª edição, São Paulo, Pearson, 1987, pp. 41 - Modificada

Determinar a condição para x ,   y ,   z ,   w de modo que ( x ,   y ,   z ,   w ) seja combinação linear de   v 1 → = ( 1 ,   - 3 ,   2,2 ) e   v 2 → = ( 2 ,   4 ,   - 1 , - 1 ) .

Passo 1

Ok, vamos começar escrevendo  ( x ,   y ,   z ,   w ) como C L de   v 1 → e   v 2 → !

Ficaria assim:

( x ,   y ,   z ,   w ) = a v 1 → + b v 2 →

x ,   y ,   z ,   w = a 1 ,   - 3 ,   2,2 + b 2,4 ,   - 1 , - 1

Abrindo em um sisteminha,

x = 1 a + 2 b     I y = - 3 a + 4 b     I I z = 2 a - 1 b     I I I w = 2 a - 1 b     ( I V )

Agora vamos tentar achar uma relação entre x ,   y ,   z , e w sem os a ' s e b ' s (vamos tentar zerar esses caras)

Fazendo I - ( I I ) , obtemos:

x - y = 1 a + 2 b - - 3 a + 4 b

x - y = 1 a + 2 b + 3 a - 4 b

x - y = 4 a - 2 b

Vamos guardar esse resultado! Ainda precisamos colocar z e w nessa relação!

Fazendo x - y - I I I - ( I V ) ,

x - y - z - w = 4 a - 2 b - 2 a - 1 b - 2 a - 1 b

x - y - z - w = 4 a - 2 b - 2 a + b - 2 a + b

x - y - z - w = 0

Também sabemos que z = w , já que as equações I I I e I V são iguais!

Substituindo isso na nossa relação aqui de cima, ficamos com:

x - y - w - w = 0

x - y - 2 w = 0

Uhull!! Achamos a nossa relação!

Mas o que fazemos com ela??

Se liga no passo 2!

Passo 2

Pensa comigo, o vetor ( x ,   y ,   z ,   w ) só será C L de   v 1 → e   v 2 → se o sistema gerado por:

x ,   y ,   z ,   w = a 1 ,   - 3 ,   2,2 + b 2,4 ,   - 1 , - 1

Possuir solução. E, esse sistema só terá solução se x - y - 2 w = 0 (já que obtivemos essa relação baseada justamente no fato de o sistema ter solução).

Então, todos os vetores x ,   y ,   z ,   w ∈ R 4 obedecerão a equação x - y - 2 w = 0 !

Para ficar mais bonitinho, podemos escrever:

x - y - 2 w = 0

x = y + 2 w

E, já sabemos que z = w .

Logo, os vetores serão da forma:

( y + 2 w ,   y ,   w ,   w )

Achamos nossa relação!! Showww de bolinhas!

Resposta

Os vetores serão da forma:

( y + 2 w ,   y ,   w ,   w )

Exercício Resolvido #6

Elaboração própria.

Escreva o vetor   v → = ( 0,0 , 0,0 ) como combinação linear dos vetores  v 1 → = ( 1 ,   0 ,   0,0 ) ,  v 2 → = ( 0 ,   1 ,   0,0 ) ,   v 3 → = ( 2 ,   - 1 ,   3 ,   2 ) ,   v 4 → = ( 1 ,   2 ,   3 ,   1 ) .

Passo 1

Belezinha, vamos começar escrevendo   v → como C L de   v 1 → ,  v 2 → ,  v 3 → e  v 4 → !

Ficaria assim:

v → = a v 1 → + b v 2 → + c v 3 → + d v 4 →

0 ,   0 ,   0 ,   0 = a 1 ,   0 ,   0,0 + b 0,1 ,   0,0 + c 2 ,   - 1 ,   3 ,   2 + d 1 ,   2 ,   3 ,   1

Abrindo em um sistema,

0 = 1 a + 2 c + 1 d     I 0 = 1 b + - 1 c + 2 d     I I 0 = 3 c + 3 d   I I I 0 = 2 c + 1 d     ( I V )

De ( I I I ) tiramos que d = - c   ( i )

Substituindo em ( I V ) :

0 = 2 c + - c

c = 0

Logo, d = 0

Se substituirmos esses valores em ( I ) e ( I I ) , também vamos achar a = 0 e b = 0 .

Então, nossa C L fica:

0 ,   0 ,   0 ,   0 = 0 1 ,   0 ,   0,0 + 0 0,1 ,   0,0 + 0 2 ,   - 1 ,   3 ,   2 + 0 1 ,   2 ,   3 ,   1

Resposta

0 ,   0 ,   0 ,   0 = 0 1 ,   0 ,   0,0 + 0 0,1 ,   0,0 + 0 2 ,   - 1 ,   3 ,   2 + 0 1 ,   2 ,   3 ,   1

Exercícios de Livros Relacionados

Sejam A = (1, 2, 3), B = (3, −1, 2), C = (4, 3, −1) e D = (5, −15, 6). Mostre que os vetores u=A B → ,v=A C →ew=A D → são linearmente dependentes e ache a equação de um plano que contenha os pontos A,
Seja E = e → 1 , e → 2 , e → 3 uma base . Sejam f 1 → = e → 1 - e → 2 + e → 3 , f 2 → = e → 2 + e → 3 e f 3 → = - 2 e → 3 (a)Mostre que F = ( f 1 → , f 2 , → f 3 → ) também é uma base.
Seja B = u → 1 , u → 2 , u → 3 uma base de V . (b)Se a → = 1 , - 3,2 B , quais são as coordenadas de a → na base C ?
Dadas as bases: E = ( - 1,1 , 0 B , 1,1 , 2 B , - 1,0 , 1 B ) e F = 0,1 , 1 E , 1,2 , - 1 E , 2 , - 1,0 E , determine na base B as coordenadas de v → = - 1,2 , - 3 E - - 2,1 , 1 F
Seja B = (vec u_1 , vec u_2 , vec u_3) uma base de V . (a)Demonstre que C = (vec v_1 , vec v_2 , vec v_3) , com vec v_1 = vec u_1 + 2 vec u_2 + vec u_3 , vec v_2 = vec u_1 - vec u_2 - vec u_3 e vec v_