Determine as reações de apoio de um pórtico que suas fibras externas estão a uma temperatura de 0°C e as fibras internas estão a uma temperatura de 80°C.
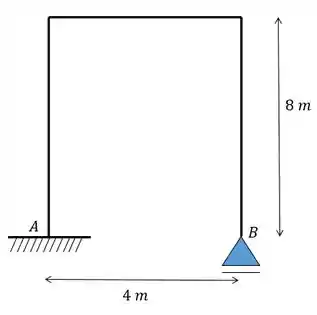
Passo 1
Fala pessoal!! agora vamos resolver um exercício que trata sobre a influência da temperatura nos pórticos. Para achar as reações dos apoios como o problema pede e resolver essa questão a gente precisa primeiro dividir essa estrutura numa estrutura isostática.
Depois de fazer essa divisão nós vamos calcular o deslocamento imposto pela temperatura e finalmente achar o hiperestático, de forma a calcular as reações. Então partiu!
Passo 2
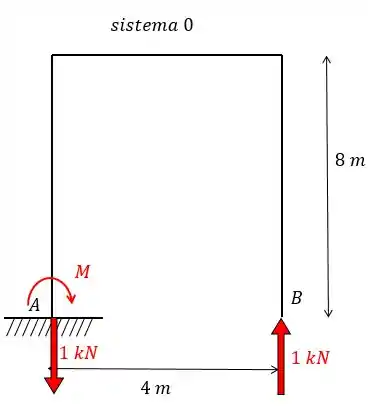
Quebrando essa estrutura de forma a obter uma estrutura isostática vamos ter.
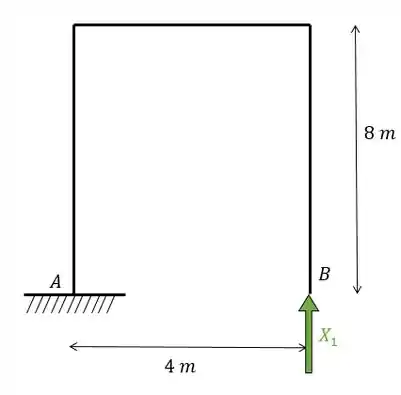
E até aqui a gente sabe resolver de boas, o que aparece de novo é o seguinte.
Pra determinar a deformação no sistema zero, que nesse caso é uma variação de temperatura, precisamos obrigatoriamente colocar uma carga unitária no mesmo lugar, na mesma direção e no mesmo sentido do hiperestático, porém iremos calcular a deformação de maneira DIFERENTE do que fazemos com o hiperestático.
Apesar da carga estar na mesma posição e sentido do hiperestático, para o hiperestático iremos calcular o diagrama de momentos, porém para o sistema zero iremos calcular as deformações de temperatura. Parece meio embolado, mas é bem tranquilo, me segue aqui.
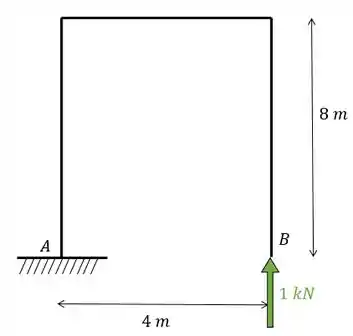
Passo 3
Como eu disse, no sistema zero colocamos uma carga unitária na mesma posição, direção e sentido do hiperestático, com isso teremos.
sabemos que para cálculo da deformação pela temperatura usamos a seguinte equação:
Que podemos simplificar de acordo como o tipo de estrutura, no nosso caso como se trata de um pórtico devemos considerar ambas as contribuições. Mas podemos simplificar como:
E sabemos que a integral do momento devido a carga unitária, integrado no comprimento S da barra, assim como o normal, nada mais são que as áreas dos respectivos diagramas, ou seja, nossa fórmula passa a ser.
Em que:
Como sabemos, iremos usar exatamente a carga unitária na mesma posição do hiperestático. Dessa maneira teremos que:
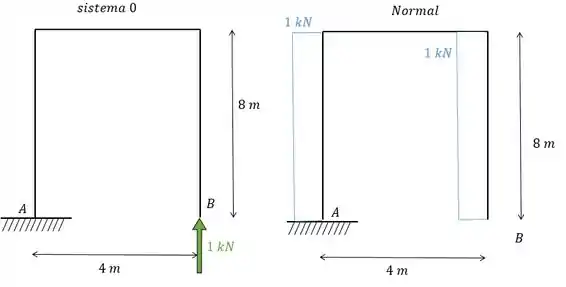
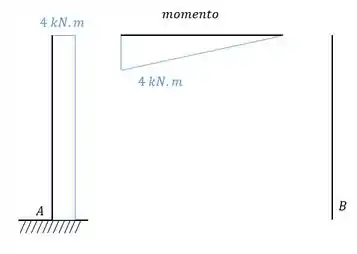
Sendo assim podemos determinar que:
Sempre que houver compressão ou o momento tracionar as fibras superiores as aréas levaram consigo os seus sinais.
OBS: É MUITO IMPORTANTE TOMAR CUIDADO COM O SINAL DAS ÁREAS, ENTÃO PRA FICAR BEM FACIL SEMPRE LMEBRE DO SEGUINTE.
- NORMAIS
- MOMENTOS FLETORES
Sempre que for compressão o sinal da área será negativo, e sempre que for tração o sinal da área será positivo.
Sempre que os momentos fletores tracionarem as fibras da parte de cima, ou as fibras externas, o sinal da área vai ser negativo, mas se tracionar as fibras da parte de baixo, ou as fibras internas, o sinal das áreas vai ser positivo.
Tome muito cuidado para não errar os sinais.
Passo 4
Agora vamos partir para a parte da temperatura.
Sabemos também que:
e por fim determinamos o valor de que será dado pela média simples dado que a geometria é regular
Substituindo na equação teremos que:
Passo 5
O sistema 1 continua sendo calculado como sempre fizemos. Analisamos a estrutura com a ação de um hiperestático unitário, determinamos o diagrama e determinamos tudo que for referente ao sistema 1, dessa maneira obtemos que:
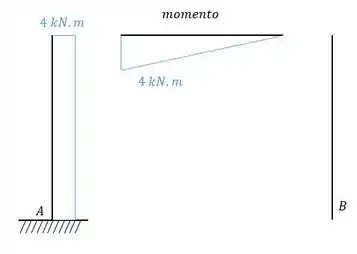
E para determinar faremos
Como , teremos que
E assim teremos que o nosso sistema será:
Substituindo teremos que
Passo 6
Determinando as reações de apoio teremos que:
Vale lembrar que em estruturas isostáticas, tanto a variação de temperatura quanto o recalque produzem reações de apoio idênticas a zero, sendo assim sempre iremos zerar o primeiro termo.
Para o momento