Método de Taylor
Produzido por Bruno PestanaTeoria
Fala aí! Bora aprender o Método de Taylor?!
Pra a gente começar com tudo, eu gostaria que você me dissesse como poderíamos resolver esse problema de valor inicial (PVI):
Ache
Poderíamos usar o método de Euler, mas confia em mim, o resultado usando o método de Taylor é muito mais preciso!
E é esse novo método que vamos aprender hoje! 🤩🤩🤩
Segundo o método de Taylor conhecendo as derivadas de uma função
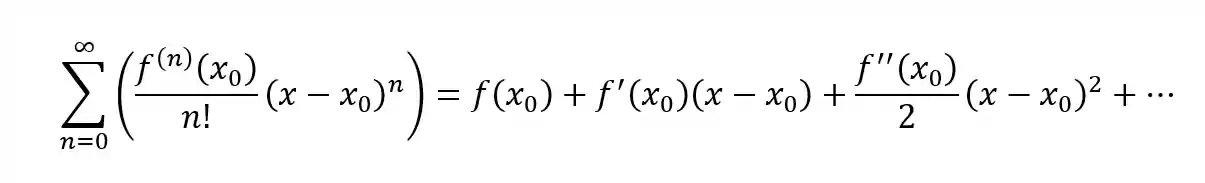
Só que é claro que a gente não vai ficar calculando derivadas infinitas, vamos truncar a série de Taylor em algum momento! 😅
Dessa forma o erro de truncamento pode ser calculado por:
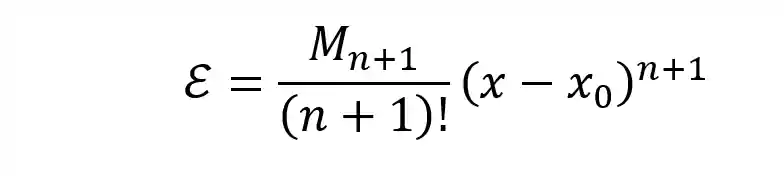
Onde
Como resolver EDO’s usando o Método de Taylor?
Vamos aprender resolvendo aquele exemplo lá do início!
Ache
A primeira coisa que vamos fazer é definir o passo,
Para
Estamos trabalhando no intervalo
Onde:
Então temos:
E queremos
Já que
Então, vamos lá:
Continuando:
Aweee! Achamos nosso
Algoritmo para o Método de Taylor
- Defina o passo
- Defina o intervalo em que vamos estimar
- Pegamos a expressão:
- Calculamos
e - Pegamos um vetor
onde vamos guardar os valores de e fazemos . - Pra
entre e fazemos
Agora que você tá sacando tudo sobre o Método de Taylor, bora praticar com exercícios?
Como resolver EDO’s usando o Método de Taylor?
Algoritmo para o Método de Taylor
Exercícios Resolvidos
Exercício Resolvido #1
Ruggiero, M. A. e Lopes, V. L. R. Cálculo Numérico: aspectos teóricos e computacionais. 2 ed.São Paulo: Pearson Makron Books, 1996. Cápitulo 8. Exercício 22.(Adaptado)
Apresente a fórmula de iteração para o método de Taylor de ordem 2 aplicado ao PVI:
Sendo
Passo 1
Aqui nem temos que fazer tantas contas assim! Ele só nos pediu a fórmula de iteração!
Lembrando que no caso geral ela é:
Passo 2
Vamos calcular as derivadas necessárias:
Daí, a fórmula de iteração fica:
Resposta
Exercício Resolvido #2
Márcia A. Gomes Ruggiero e Vera Lúcia da Rocha Lopes, Cálculo Numérico – Aspectos Teóricos e Computacionais, 2ª ed. São Paulo: MAKRON Books, 1996, pag 325, exemplo 2 adaptado.
Calcular usando a série de Taylor de 2ª ordem para o PVI:
Passo 1
Fala, td blz? Esse assunto de resolver PVI com série de Taylor é muita viagem né, mas vamos por partes, pode ficar tranquilo. Olha lá, a primeira coisa a se fazer é isolar o na sua EDO.
Esse negócio que ficou sozinho do lado direito da igualdade vamos chamar de , ok?
E já vamos calcular logo de cara o , que é parte da fórmula pra achar ,
com os dados de e que a gente tira do PVI alí no enunciado.
Passo 2
Agora temos que encontrar o . Como seu professor pediu ordem 2, essa vai ser a última derivada que você precisa achar. Pra isso vamos aplicar a regrinha da cadeia hehe
Vamos por pedacinho então
E
Então temos
Agora precisamos calcular , que é parte da fórmula pra achar .
Passo 3
Agora precisamos substituir esses valores que encontramos na fórmula do método que é essa aqui oh:
Adaptada pro nosso problema, ela fica assim:
Resposta
Exercício Resolvido #3
Listas de exercício – UNESP - Adaptado
Calcular usando a série de Taylor de 2ª ordem para o PVI:
Considere
Passo 1
Fala, td blz? Doideraaa resolver PVI com série de Taylor, mas vamos lá!! Primeiro, Esse negócio que ficou sozinho do lado direito da igualdade vamos chamar de , ok?
Sabemos também lá da teoria que para achar , teremos que achar primeiro então olha lá.
Então bora calcular esse
Beleza, a última parcela que falta é , mas pra acha-la vamos precisar de uma ajudinha da regra da cadeia
Por partes, e com calma vamo lá.
E
Então
Aeeew!! Agora basta encontrar
Então já podemos achar .
Passo 2
Já estamos quase lá, agora é só aplicar mais uma iteração pra chegar em
Podemo calcular .
E rapidão já calcular .
E pra acabar, e tirar aquele 10, basta agora usar de novo a equação do método que a gente montou lá no começo.