Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Método de Euler Aperfeiçoado

Ver Todos os Exercícios

Teoria

E aí meus caros, bora entender mais um assuntinho de numérico envolvendo resolução de EDO´s. Espero que você ainda lembre do método de Euler, pois vamos continuar falando dele.

Então chega mais, que aqui é só sucesso!

Antes de começas, é importante saber que esse método pode ter outros nomes conhecidos: método de Euler modificado e método de Heun.

Vamos dar uma olhadinha aqui, só pra relembrar. O método de Euler é um método iterativo, ou seja, onde uma etapa do cálculo depende da anterior até que a gente chegue no resultado. Tranquilo né?

O método de Euler tenta aproximar o valor exato da função y ( t n ) através da reta tangente no ponto ( t n , y ( t n ) ) mais ou menos assim:

y - y 0 = m ( t - t 0 )

Esse valor m   é a inclinação da reta tangente, e dentro do cálculo, a função que tem a ver com a reta tangente é??? Isso mesmo, a derivada. Então m y ' ( t 0 ) =   f ( x 0 ,   y 0 ) . Isso é uma informação importantíssima e você já vai sacar o motivo!

Se liga só:

Fazendo algumas considerações tipo: que o passo h será uniforme h = t - t 0 , entre pontos t 1   ,   t 2 …   t n , dentro de um intervalo temos: y n + 1 = y n + h f ( t n , y n )

Basicamente, no método de Euler convencional

Maaaaaaaaaaas, esse assunto é para falar do método de Euler Aperfeiçoado, então meu consagrado, vamos melhorar esse negócio.

O método convencional utilizava uma retinha tangente e tals, e nesse vamos fazer o que????????

Aqui nós determinamos duas derivadas (ou seja, duas retas tangentes) para o intervalo, uma no ponto inicial e outra no ponto final.

E qual das duas nós usamos no cálculo? As duas ué, só que nesse caso nós pegamos a média entre elas.

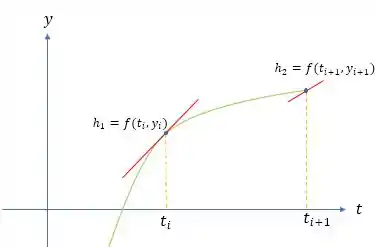
Veja que h 1 é a inclinação no início do intervalo e h 2 no final do intervalo. Vamos adicionar algumas coisas nela e deixar assim oh:

y n + 1 = y n + h 2 f t n , y n + f t n + 1 , y n + h f t n , y n

Lembrando que f t n , y n = y n ' !

Até aí tudo bem né? Nós só acrescentamos uma tangente a mais.

E o erro vai ser o seguinte:

E x = h 2 3 ! y ' ' ' ξ x

Mas, é aquela velha história, que interessa mesmo pra gente é o limitante do erro:

E x ≤ h 2 3 ! M 3

onde M 3 é o valor máximo (aplicado ao intervalo) da terceira derivada.

M 3 = max x ∈ x 0 , x ⁡ f ' ' ' x .

Só pra ter certeza que ficou tudo cristalino vamos ver um exemplo. Resolve aí!

y ' - 3 y + 5 - t 2 = 0

0 ≤ t ≤ 1

y 0 = 1

h = 0.2

Começamos isolando nosso y ' :

y ' = f t n , y n = 3 y - 5 + t 2

E temos que t n + 1 = t n + h . Agora jogamos na fórmula:

y 1 = y 0 + h 2 f t 0 , y 0 + f t 1 , y 0 + h f t 0 , y 0

Agora para não ficar muito embolado eu recomendo resolver separadamente:

y 0 + h f t 0 , y 0 = y 0 + h 3 y 0 - 5 + t 0 2 = 1 + 0.2 3 1 - 5 + 0 2 = 0.6

f t 1 , y 0 + h f t 0 , y 0 = f 0.2,0.6 = 3 0.6 - 5 + 0.2 2 = - 3.16

f t 0 , y 0 = 3 y 0 - 5 + t 0 2 = 3 1 - 5 + 0 2 = - 2

Juntando tudo:

y 1 = y 0 + h 2 f t 0 , y 0 ⏟ - 2 + f t 1 , y 0 + h f t 0 , y 0 ⏟ - 3.16 = 1 + 0.1 - 5.16 = 0.484

Então acabamos de descobrir que y 0.2 = 0.484 !

Para achar os outros é só continuar o processo 😉

Algoritmo

O algoritmo não vai mudar muito do de Euler normal não. Só precisamos adicionar aquela parcela.

Passo 1. Dados iniciais (o que seu programa vai receber de você):

  1. Passo h
  2. Intervalo em que vamos estimar f , x 0 , x f
  3. Valor inicial y 0

Passo 2. Definimos um vetor y onde vamos guardar as estimativas de f , de modo que y 0 = y 0

Passo 3. Definimos um vetor x formado pelos pontos onde vamos estimar as derivadas.

Passo 4. Definimos n = x f - x 0 h

Passo 5. Para i de 0 a n - 1 repita os passos 6 e 7.

Passo 6. k = y i + h f x i , y i

Passo 7. y i + 1 = y i + h 2 f x i , y i + f x i + h , k

Pra finalizar é só retornar o vetor y ! Fica a dica também que existem diferentes entradas possíveis para esse método. As que eu usei são só um exemplo. Você poderia entrar, por exemplo, com o x 0 , o passo h e o valor n ao invés de entrar com o intervalo. Outra opção era entrar diretamente com o vetor x pronto. Nesse caso não seria necessário dar nem o passo nem o intervalo.

Algoritmo

Exercícios Resolvidos

Exercício Resolvido #1

Lista 6 – Professor Mauro – UFRJ – Questão 1 Adaptada

Determine uma aproximação para y 1 na seguinte Equação Diferencial Ordinária, com o passo h = 0.2 pelo método de Euler Aperfeiçoado:

y ' x + 2 y x = 0           ∀ x ∈ 0,1 y 0 = 1

Passo 1

Pelas informações que ele nos deu temos:

y ' = - 2 y

y 0 = 1

x 0 = 0

E com passo h = 0.2 teremos o seguinte:

Agora é só jogar na fórmula e ser feliz:

y n + 1 = y n + h 2 f x n , y n ⏟ k 1 n + f x n + 1 , y n + h f x n , y n ⏟ k 2 n

Iteração 1 x = 0.2 :

k 1 0 = f x 0 , y 0 = - 2 y 0 = - 2

k 2 0 = f x 1 , y 0 + h k 1 0 = - 2 y 0 + h k 1 0 = - 1.2

y 1 = y 0 + h 2 k 1 0 + k 2 0 = 0.68

Iteração 2 x = 0.4 :

k 1 1 = f x 1 , y 1 = - 2 y 1 = - 1.36

k 2 1 = f x 2 , y 1 + h k 1 1 = - 2 y 1 + h k 1 1 = - 0.816

y 2 = y 1 + h 2 k 1 1 + k 2 1 = 0.4624

Iteração 3 x = 0.6 :

k 1 2 = f x 2 , y 2 = - 2 y 2 = - 0.9248

k 2 2 = f x 3 , y 2 + h k 1 2 = - 2 y 2 + h k 1 2 = - 0.55488

y 3 = y 2 + h 2 k 1 2 + k 2 2 = 0.31443

Iteração 4 x = 0.8 :

k 1 3 = f x 3 , y 3 = - 2 y 3 = - 0.62886

k 2 3 = f x 4 , y 3 + h k 1 3 = - 2 y 3 + h k 1 3 = - 0.37732

y 4 = y 3 + h 2 k 1 3 + k 2 3 = 0.21381

Iteração 5 x = 1 :

k 1 4 = f x 4 , y 4 = - 2 y 4 = - 0.42763

k 2 4 = f x 5 , y 4 + h k 1 4 = - 2 y 4 + h k 1 4 = - 0.25658

y 5 = y 4 + h 2 k 1 4 + k 2 4 = 0.14539

Passo 2

Ufa, chegamos na nossa aproximação!

y 1 ≅ 0.14539

Resposta

y 1 ≅ 0.14539

Exercício Resolvido #2

Lista 7 – Professora Angela – UFRJ – Questão 3

Determine uma aproximação para y 1.2 sabendo que y x é solução da equação diferencial:

y ' = y 2 + x y 1 = 1

usando o método de Euler aperfeiçoado, com h = 0.1

Passo 1

Temos que:

y ' = y 2 + x

y 0 = 1

x 0 = 1

E com passo h = 0.1 teremos o seguinte:

Aplicando a fórmula:

y n + 1 = y n + h 2 f x n , y n ⏟ k 1 n + f x n + 1 , y n + h f x n , y n ⏟ k 2 n

Iteração 1 x = 1.1 :

k 1 0 = f x 0 , y 0 = y 0 2 + x 0 = 2

k 2 0 = f x 1 , y 0 + h k 1 0 = y 0 + h k 1 0 2 + x 1 = 2.54

y 1 = y 0 + h 2 k 1 0 + k 2 0 = 1.227

Iteração 2 x = 1.2 :

k 1 1 = f x 1 , y 1 = y 1 2 + x 1 = 2.60553

k 2 1 = f x 2 , y 1 + h k 1 1 = y 1 + h k 1 1 2 + x 2 = 3.41281

y 2 = y 1 + h 2 k 1 1 + k 2 1 = 1.52792

Passo 2

Pronto, nossa aproximação é:

y 1.2 ≅ 1.52792

Resposta

y 1.2 ≅ 1.52792

Exercício Resolvido #3

Lista 7 – Professor Angela – UFRJ – Questão 4 Adaptada

Dado o P V I :

y ' = x 2 y - y y 0 = 1

Calcule uma aproximação para y 0.5 com h = 0.25 usando o método de Euler Aperfeiçoado.

Passo 1

Temos:

y ' = x 2 y - y

y 0 = 1

x 0 = 0

E com passo h = 0.25 teremos o seguinte:

Só jogar na fórmula e fim de papo:

y n + 1 = y n + h 2 f x n , y n ⏟ k 1 n + f x n + 1 , y n + h f x n , y n ⏟ k 2 n

Iteração 1 x = 0.2 5 :

k 1 0 = f x 0 , y 0 = x 0 2 y 0 - y 0 = - 1

k 2 0 = f x 1 , y 0 + h k 1 0 = x 1 2 y 0 + h k 1 0 - y 0 + h k 1 0 = - 0.70313

y 1 = y 0 + h 2 k 1 0 + k 2 0 = 0.78711

Iteração 2 x = 0 . 5 :

k 1 1 = f x 1 , y 1 = x 1 2 y 1 - y 1 = - 0.73792

k 2 1 = f x 2 , y 1 + h k 1 1 = x 2 2 y 1 + h k 1 1 - y 1 + h k 1 1 = - 0.45197

y 2 = y 1 + h 2 k 1 1 + k 2 1 = 0.63837

Passo 2

E chegamos na nossa aproximação:

y 0.5 ≅ 0.63837

Resposta

y 0.5 ≅ 0.63837

Exercício Resolvido #4

Lista 7 – Professora Luziane – UFRJ – Questão 2 Adaptada

Dado o P V I : y ' = 4 - 2 x ,   y 0 = 2 . Considere h = 0.25 e h = 0.1 .

a Encontre uma aproximação para y 0.5 usando o método de Euler Aperfeiçoado para cada h .

b Compare seus resultados com a solução exata dada por y x = - x 2 + 4 x + 2 .

Passo 1

a Temos o seguinte:

y ' = 4 - 2 x

y 0 = 2

x 0 = 0

E com passo h = 0.25 teremos o seguinte:

Aplicando a formuleta:

y n + 1 = y n + h 2 f x n , y n ⏟ k 1 n + f x n + 1 , y n + h f x n , y n ⏟ k 2 n

Iteração 1 x = 0.25 :

k 1 0 = f x 0 , y 0 = 4 - 2 x 0 = 4

k 2 0 = f x 1 , y 0 + h k 1 0 = 4 - 2 x 1 = 3.5

y 1 = y 0 + h 2 k 1 0 + k 2 0 = 2.9375

Iteração 2 x = 0.5 :

k 1 1 = f x 1 , y 1 = 4 - 2 x 1 = 3.5

k 2 1 = f x 2 , y 1 + h k 1 1 = 4 - 2 x 2 = 3.0

y 2 = y 1 + h 2 k 1 1 + k 2 1 = 3.75

Logo, temos y 0.5 ≅ 3.75

Passo 2

Agora com h = 0.1 :

Iteração 1 x = 0.1 :

k 1 0 = f x 0 , y 0 = 4 - 2 x 0 = 4

k 2 0 = f x 1 , y 0 + h k 1 0 = 4 - 2 x 1 = 3.8

y 1 = y 0 + h 2 k 1 0 + k 2 0 = 2.39

Iteração 2 x = 0.2 :

k 1 1 = f x 1 , y 1 = 4 - 2 x 1 = 3.8

k 2 1 = f x 2 , y 1 + h k 1 1 = 4 - 2 x 2 = 3.6

y 2 = y 1 + h 2 k 1 1 + k 2 1 = 2.76

Iteração 3 x = 0.3 :

k 1 2 = f x 2 , y 2 = 4 - 2 x 2 = 3.6

k 2 2 = f x 3 , y 2 + h k 1 2 = 4 - 2 x 3 = 3.4

y 3 = y 2 + h 2 k 1 2 + k 2 2 = 3.11

Iteração 4 x = 0.4 :

k 1 3 = f x 3 , y 3 = 4 - 2 x 3 = 3.4

k 2 3 = f x 4 , y 3 + h k 1 3 = 4 - 2 x 4 = 3.2

y 4 = y 3 + h 2 k 1 3 + k 2 3 = 3.44

Iteração 5 x = 0.5 :

k 1 4 = f x 4 , y 4 = 4 - 2 x 4 = 3.2

k 2 4 = f x 5 , y 4 + h k 1 4 = 4 - 2 x 5 = 3

y 5 = y 4 + h 2 k 1 4 + k 2 4 = 3.75

E nossa aproximação aqui vai ficar:

y 0.5 ≅ 3.75

Passo 3

A solução exata é:

y x = - x 2 + 4 x + 2

y 0.5 = 3.75

Como podemos ver, ambas as nossas aproximações bateram com o valor exato da função naquele ponto. Isso pode ser explicado pela fórmula do erro! Temos:

E x = h 2 3 ! y ' ' ' ξ x

Como nossa função y x é de segundo grau, sua derivada terceira é zero! Logo, o erro será zero independente do h escolhido.

Resposta

Para h = 0.25 , y 0.5 ≅ 3.75 .

Para h = 0.1 , y 0.5 ≅ 3.75 .

O valor exato da função é y 0.5 = 3.75 . Logo, nossas aproximações bateram com o valor exato. Ver explicação acima.

Exercício Resolvido #5

Lista de exercícios - FEI

Calcular a EDO:

y ' = y + e x

No intervalo 0 ≤ x ≤ 1 , para y 0 = 0 e passo h = 0.5 . Resolver pelo método de Euler Aperfeiçoado.

Passo 1

Bom a gente precisa escrever as equações adaptadas ao problema. Então bora lá, tudo que tem y ' tem que estar do lado esquerdo da igualdade, enquanto tudo o que não tem linha deve estar do lado direito da igualdade. Dessa forma, a EDO vai estar escrita assim oh:

y ' = f ( x , y )

Nesse nosso exercício o professor já deu a EDO nesse estilinho. =)

As equações do método de euler aperfeiçoado adaptadas a esse problema ficam desse jeito aqui:

K 1 = f x , y = y ( x ) + e x

Beleza essa primeira foi fácil, é só copiar a f x , y . Shooow!

K 2 = f ( x + h ,   y + h * K 1 )

Começou a ficar meio feio né. Mas o que essa fórmula aí quer dizer é o seguinte:

- Onde tiver escrito x , escreva x + h ;

- Onde tiver escrito y , escreva y + h * K 1 . E esse K 1 é o resultado da primeira equação e h é o passo que o professor pediu.

Então, a equação ficou assim oh!

K 2 = e x + h + y + h * K 1

K 2 = e x + 0.5 + y + 0.5 * K 1

A última equação, vai ser aquela que a gente usa para achar o valor de y .

y x + h = y x + h 2 ( K 1 + K 2 )

y x + 0.5 = y x + 0.5 2 ( K 1 + K 2 )

Agora que já temos as equações adaptadas ao nosso problema vamos construir uma tabela pra facilitar nossa vida

Passo 2

A tabela é essa aqui oh:

Percebe que o passo na linha do x é h = 0.5 e sabemos do enunciado que y 0 = 0 que tá alí na primeira linha do y . As outras duas linhas são pra cada K que calcularmos. Beleza?!

Bora por a mão na massa então. É só aplicar as equações adaptadas para completar a tabela.

Coluna: x = 0

K 1 = 0 + e 0 = 1

K 2 = e 0.5 + 0 + 0.5 * 1 = 2.1487

Agora a gente aplica a equação para encontrar o próximo y .

y 0.5 = 0 + 0.5 2 1 + 2.1487 = 0.7872

Agora Coluna: x = 0.5

K 1 = 0.7872 + e 0.5 = 2.4359

K 2 = e 1 + 0.7872 + 0.5 * ( 2.4359 ) = 4.7234

y 1 = 0.7872 + 0.5 2 2.4359 + 4.7234 = 2.577

Resposta

y 1 = 2.577

Exercício Resolvido #6

Lista de exercícios - FEI

Dada a equação diferencial T ' = t . c o s ( t + T ) calcule 𝑇(2) e 𝑇(3) com 3 casas decimais, usando o método de Euler Aperfeiçoado. Para t=1, temos T=3. Escrever as fórmulas adaptadas à questão.

Passo 1

Faala aeee, de cara já temos que olhar como a nossa EDO foi dada pelo professor. O ideal é que ela esteja separadinha, T ' de um lado e f ( t , T ) do outo. Dessa forma, a EDO vai estar escrita assim oh:

T ' = f ( t , T )

Nesse nosso exercício tá tudo lindo, o professor já deu a EDO nesse formato.

Agora precisamos escrever as equações do método de euler aperfeiçoado adaptadas a esse problema.

K 1 = f t , T = t . c o s ( t + T )

Beleza essa primeira foi fácil, é só copiar a f t , T . Já a equação de K 2   é um pouco mais escrotinha, o formato dela é esse aqui:

K 2 = f ( t + h ,   y + h * K 1 )

Caaalma, essa equação do demoooo quer dizer o seguinte oh:

- Onde tiver escrito t , escreva t + h ;

- Onde tiver escrito T , escreva T + h * K 1 . E esse K 1 é o resultado da primeira equação e h é o passo que o professor pediu.

Então, a equação ficou assim oh!

K 2 = t + 1 * c o s ⁡ [ t + 1 + ( T + K 1 ) ]

A última equação, vai ser aquela que a gente usa para achar o valor de y .

y t + h = y t + h 2 ( K 1 + K 2 )

y t + 1 = y t + 1 2 ( K 1 + K 2 )

Bora por tudo isso numa tabelinha então pra gente não se perder com tanta coisa.

Passo 2

A tabela é essa aqui oh:

Na primeira linha o passo é h = 1 e sabemos do enunciado que T 1 = 3 que tá alí na primeira linha do T . Agora precisaremos encontrar K 1 e K 2   para encontrarmos T ( 2 ) e T ( 3 ) .

Bora por a mão na massa então. É só aplicar as equações adaptadas para completar as colunas da tabela.

Coluna t = 1 :

K 1 = t * c o s ( t + T )

K 1 = 1 * c o s 1 + 3 = - 0.654

K 2 = t + 1 * c o s ⁡ [ t + 1 + ( T + K 1 ) ]

K 2 = 2 * cos ⁡ 2 + 3 + - 0.654 = - 0.716

Agora a gente aplica a equação para encontrar T ( 2 ) .

T 2 = 3 + 1 2 - 0.654 - 0.716 = 2.315

Agora é só jogar tudo na tabelinha.

Agora só ficou faltando achar o T ( 3 ) .

Bora pra próxima coluna t = 2 :

K 1 = t * c o s ( t + T )

K 1 = 2 * c o s 1 + 2.315 = - 0.774

K 2 = t + 1 * c o s ⁡ [ t + 1 + ( T + K 1 ) ]

K 2 = 3 * cos ⁡ 3 + 2.315 + - 0.774 = - 0.509

Agora a gente aplica a equação para encontrar T ( 3 ) .

T 3 = 2.315 + 1 2 - 0.774 - 0.509 = 1.674

Agora foiii hein, calculamos tudo!! Bora colocar na tabelinha.

Resposta

T 2 = 2.315

T 3 = 1.674

Exercício Resolvido #7

Lista de exercícios - FEI

Calcular a EDO:

y ' = 1 x + y

No intervalo 1 ≤ x ≤ 2 , para y 0 = 2 e passo h = 0.5 . Resolver pelo método de Euler aperfeiçoado.

Passo 1

Faala aeee, já estamos com sorte logo de cara. O ideal é que a EDO esteja separadinha, y ' de um lado e f ( x , y ) do outo. Assim, a EDO deve estar escrita assim oh:

y ' = f ( x , y )

Nesse nosso exercício tá tudo lindo, o professor já deu a EDO nesse formato.

Agora precisamos escrever as equações do método de euler aperfeiçoado adaptadas a esse problema.

K 1 = f x , y = 1 x + y

A primeira foi só tranquilidade, é só copiar a f x , y . Já a equação de K 2   é mais barra pesada, o formato dela é esse aqui:

K 2 = f ( t + h ,   y + h * K 1 )

Caaalma, essa equação do demoooo quer dizer o seguinte oh:

- Onde tiver escrito x , escreva   x + h ;

- Onde tiver escrito y , escreva y + h * K 1 . E esse K 1 é o resultado da primeira equação e h é o passo que o professor pedir.

Então, a equação ficou assim oh!

K 2 = 1 ( x + h ) + ( y + h * K 1 )

Como o passo h = 0.5 , temos:

K 2 = 1 ( x + 0.5 ) + ( y + 0.5 * K 1 )

A última equação, vai ser aquela que a gente usa para achar o valor de y .

y t + h = y t + h 2 ( K 1 + K 2 )

y t + 0.5 = y t + 0.5 2 ( K 1 + K 2 )

Vamos por todos os resultados numa tabelinha, pq a gente não é obrigado né a decorar tudo isso.

Passo 2

A tabela é essa aqui oh:

Na primeira linha o passo é h = 0.5 e sabemos do enunciado que y 1 = 2 que tá alí na primeira linha do y . Agora precisaremos encontrar K 1 e K 2   para encontrarmos y ( 1.5 ) e y ( 2 ) .

Agora é só aplicar as equações adaptadas para completar as colunas da tabela.

Coluna x = 1 :

K 1 = 1 x + y

K 1 = 1 1 + 2 = 3

K 2 = 1 ( x + 0.5 ) + ( y + 0.5 * K 1 )

K 2 = 1 ( 1 + 0.5 ) + 2 + 0.5 * 3 = 4.17

Agora a gente aplica a equação para encontrar y ( 1.5 ) .

y 1.5 = 2 + 0.5 2 3 + 4.17 = 3.792

Agora é só jogar tudo na tabelinha.

Agora só ficou faltando achar o y ( 2 ) .

Bora pra próxima coluna x = 1.5 :

K 1 = 1 x + y

K 1 = 1 1.5 + 3.792 = 4.458

K 2 = 1 ( x + 0.5 ) + ( y + 0.5 * K 1 )

K 2 = 1 ( 1.5 + 0.5 ) + 3.792 + 0.5 * 4.458 = 6.521

Agora a gente aplica a equação para encontrar y ( 2 ) .

y 2 = 3.792 + 0.5 2 4.458 + 6.521 = 6.54

Agora foiii hein, calculamos tudo!! Bora colocar na tabelinha.

Resposta

y 1.5 = 3.792

y 2 = 6.54

Exercício Resolvido #8

Lista de exercícios - FEI

Um indivíduo está recebendo uma injeção intravenosa de glicose na taxa constante de c m g m i n . É um fato biológico que, dentro de certos limites, o corpo utiliza a glicose em uma taxa proporcional à sua concentração na corrente sanguínea. A EDO que modela esta situação é: y ' t = c V - k y , onde V é o volume de sangue no corpo do indivíduo, consideraremos que a quantidade de glicose injetada não altera V apreciavelmente. A mudança da concentração de glicose no sangue é o resultado de dois fatores: um aumento devido à injeção intravenosa permanente e a redução devida à retirada da glicose sanguínea pelo corpo. Em um tempo t qualquer, a taxa de mudança de concentração devida à injeção intravenosa permanente é c V , e a taxa de mudança de concentração devida aos processos metabólicos é −𝑘𝑦, para alguma constante k positiva. Supondo c = 12   m g / m i n , V = 5 l e k = 0.12 , como calcular, pelo método de Euler aperfeiçoado, a concentração de glicose entre 10 e 14 minutos com 𝑦0 = 12.5 𝑒 ℎ = 1?

Passo 1

Oiiiie, logo de cara a gente precisa escrever as equações adaptadas ao problema. Então bora lá, tudo que tem y ' tem que estar do lado esquerdo da igualdade, enquanto tudo o que não tem linha deve estar do lado direito da igualdade. Dessa forma, a EDO vai estar escrita assim oh:

y ' = f ( t , y )

Nesse nosso exercício tá tudo lindo, o professor já deu a EDO nesse formato.

Substituindo as constantes na EDO, ficamos com:

y ' t = c V - k y

y ' t = 12 5 - 0.12 y = 2.4 - 0.12 y

As equações do método de euler aperfeiçoado adaptadas a esse problema ficam desse jeito aqui oh:

K 1 = f t , y = 2.4 - 0.12 y

Beleza essa primeira foi fácil, é só copiar a f t , y . Shooow!

Já a equação de K 2   fica assim:

K 2 = f ( t + h ,   y + h * K 1 )

Caaalma, essa equação estranha quer dizer o seguinte oh:

- Onde tiver escrito t , escreva t + h ;

- Onde tiver escrito y , escreva y + h * K 1 . E esse K 1 é o resultado da primeira equação e h é o passo que o professor pediu.

Então, a equação ficou assim oh!

K 2 = 2.4 - 0.12 * ( y + h * K 1 )

Como h = 1 , temos:

K 2 = 2.4 - 0.12 * ( y + K 1 )

A última equação, vai ser aquela que a gente usa para achar o valor de y .

y t + h = y t + h 2 ( K 1 + K 2 )

y t + 1 = y t + 1 2 ( K 1 + K 2 )

Agora que já temos as equações adaptadas ao nosso problema vamos construir uma tabela pra facilitar nossa vida

Passo 2

A tabela é essa aqui oh:

Percebe que o passo na linha do t é h = 1 e sabemos do enunciado que y 10 = 12.5 que tá alí na primeira linha do y . As outras duas linhas são pra cada K que calcularmos. Beleza?!

Bora por a mão na massa então. É só aplicar as equações adaptadas para completar as colunas da tabela.

Coluna t = 10 :

K 1 = 2.4 - 0.12 * y 10

K 1 = 2.4 - 0.12 * 12.5 = 0.9

K 2 = 2.4 - 0.12 * ( y ( 10 ) + K 1 )

K 2 = 2.4 - 0.12 * 12.5 + 0.9 = 0.792

Agora a gente aplica a equação para encontrar y ( 11 ) .

y 11 = 12.5 + 1 2 0.9 + 0.792 = 13.35

Agora é só jogar tudo na tabelinha.

Bora pra próxima coluna t = 11 :

K 1 = 2.4 - 0.12 * y 11

K 1 = 2.4 - 0.12 * 13.35 = 0.799

K 2 = 2.4 - 0.12 * ( y ( 11 ) + K 1 )

K 2 = 2.4 - 0.12 * 13.35 + 0.799 = 0.703

Só aplicar a equação para encontrar y ( 12 ) agora.

y 12 = 13.35 + 1 2 0.799 + 0.703 = 14.10

Passando pra tabelinha, que ajuda a gente a não se perder...

Bora pra próxima coluna t = 12 :

K 1 = 2.4 - 0.12 * y 12

K 1 = 2.4 - 0.12 * 14.10 = 0.708

K 2 = 2.4 - 0.12 * ( y ( 12 ) + K 1 )

K 2 = 2.4 - 0.12 * 14.10 + 0.708 = 0.623

Só aplicar a equação para encontrar y ( 13 ) agora.

y 13 = 14.10 + 1 2 0.708 + 0.623 = 14.76

Passando tudo pra tabelinha do passo-a-passo:

Bora pra ÚLTIMA coluna, t = 13 :

K 1 = 2.4 - 0.12 * y 13

K 1 = 2.4 - 0.12 * 14.76 = 0.628

K 2 = 2.4 - 0.12 * ( y ( 13 ) + K 1 )

K 2 = 2.4 - 0.12 * 14.76 + 0.628 = 0.553

Só aplicar a equação para encontrar y ( 13 ) agora.

y 13 = 14.76 + 1 2 0.628 + 0.553 = 15.35

Finalizando a tabela ficamos com:

Dá pra ver aí que encontramos as concentrações de glicose (valores de y em verde) para cada instante de tempo pedido pelo professor!! Show de Bolinhas!!

Resposta

y 11 = 13.35

y 12 = 14.10

y 13 = 14.76

y 14 = 15.35

Exercícios de Livros Relacionados

16. Considere o PVI
3. Dado o PVI abaixo, considere h = 0.5, 0.25, 0.125 e 0.1 y ' = 4 - 2 x y 0 = 2 a) Encontre uma aproximação para y ( 5 ) usando o método de Euler aperfeiçoado, para cada h .b) Compare seus resultados
21. Considere o PVI
19. Considere o problema: y ' ' + 7 y = 0 y 0 = 2 y ' 0 = 0 Com x ∈ [ 0 ,1 ] a) reescreva os métodos de Euler e Euler aperfeiçoado para resolver este problema como um sistema de equações de 1ª ordem;b
Considere o .a) Encontre a solução aproximada usando o método de Euler com h = 0.5 eh• 0.25, considerando x E [O, 2]; b) idem, usando Euler Aperfeiçoado; c) idem, usando Runge-Kutta de 41 ordem; d) sa