Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Método da Posição Falsa

Ver Todos os Exercícios

Teoria

O método da posição falsa, é um método interativo usado para aproximar zeros de funções. Nele, precisamos de um intervalo inicial que contenha a raiz e de um erro máximo que vai definir o critério de parada.

Hoje a gente vai aprender, juntinhos, tudo o que você precisa saber sobre esse método! E se você ouvir falar dele como método da falsa posição, fica tranquilo, é a mesma coisa!

Pra a gente começar com tudo, se liga nesse videozinho supercompleto que o Responde Aí preparou pra você 👇

Ou continua comigo no textinho! 👇👇👇

Métodos Interativos

O método da posição falsa é um método interativo, mas afinal, o que isso significa?

Os métodos iterativos  são métodos que a gente usa no cálculo numérico e ele consiste em, sair de um intervalo inicial meio grosseiro e refinar através de uma série de iterações até atender ao critério de parada.

Por exemplo, você tem a seguinte equação de terceiro grau:

E você quer achar suas raízes reais. Para isso você “chuta” que existe uma raiz entre e . Então vai ser seu intervalo inicial. Então o próximo passo é ir fazendo interações até o nosso critério de parada ser atingido.

O critério de parada esta relacionado ao erro que admitimos razoável na resposta final!

Se liga nesse esqueminha para o algoritmo de métodos iterativos em geral:

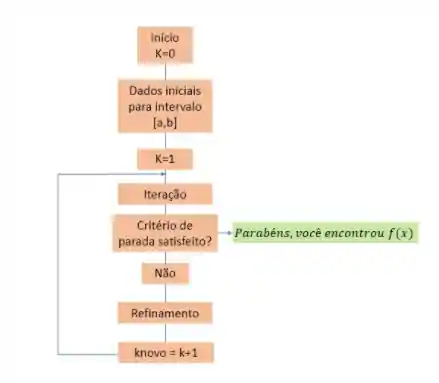
Métodos Interativos: Algoritmo Geral
Métodos Interativos: Algoritmo Geral

Como calcular método da falsa posição?

Pra começar, precisamos de um intervalo que contenha a raiz que se deseja obter, de tal forma que .

Isso a gente tira lá do isolamento de raízes! E ele precisa daquele erro que vai servir pro nosso critério de parada.

O de cada interação vai ser calculado usando a seguinte fórmula:

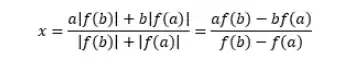
Fórmula: Método da posição falsa
Fórmula: Método da posição falsa

-Mas da onde essa fórmula saiu?

Imagina o seguinte, nós temos um intervalo . E digamos que e . Como está mais próximo de que é mais provável que a esteja mais próxima da raiz que b concorda?

E é daí que saiu essa fórmula! Ao invés de tirarmos a média aritmética entre e , nós tiramos uma média ponderada com pesos e . Assim nosso ponto vai tender mais para o que estiver mais próximo do zero! Inteligente né?

Vamos dar uma olhadinha no gráfico para ver como fica:

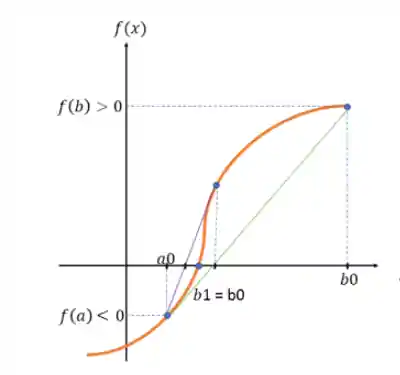
Método da posição falsa: Gráfico
Método da posição falsa: Gráfico

Perceba que, quando usamos a média ponderada, o intervalo vai convergindo mais rápido pra raiz real da função! A diferença é que aqui esses intervalos não vão ter o mesmo tamanho e provavelmente a raiz vai estar sempre no menor, o que facilita a nossa vida já que os intervalos diminuem mais rápido!


De resto, continuamos as iterações até que o critério de parada seja atingido!

-Opa, e que critério de parada usamos aqui?

Aqui é comum usarmos dois critérios e muitas vezes recebemos dois erros . O e o , de modo que paramos se algum desses critérios for satisfeito:

  • : Nesse caso basta escolhermos algum dentro de
  • ou : Nesse caso escolhemos ou como e fim de papo.


Nós costumamos fazer isso aqui pois precisamos calcular e para o cálculo de , então não custa nada usar eles haha.

No entanto, no final das contas podemos usar qualquer outro critério de parada ou só um desses aí.

Agora vamos resolver um probleminha juntos?

Exemplo: Ache uma aproximação para a raiz de entre com erros .

Beleza, então nossas informações são:

Podemos fazer nossa primeira interação, usando:

Então, substituindo, temos:

Logo, nosso novo intervalo será formado por e . Temos então que:

Verificamos nosso critério de parada:

Como não alcançamos o critério de parada continuamos as iterações.

Vamos organizar na tabelinha marota pra organizar o conteúdo e as iterações e ver como fica, Lembrando:

Tabela de resolução do método da posição falsa
Tabela de resolução do método da posição falsa

Prontinho, sucesso!

Algoritmo do Método da Falsa Posição

Então, pra resumir, o algoritmo do método da posição falsa é o seguinte:

Passo 1. Dados iniciais (o que seu programa vai receber de você):

  • Intervalo inicial contendo a raiz
  • Precisão do resultado final e

Passo 2. Definimos um contador de iterações ;

Passo 3: ?

  • Se sim, então o seu intervalo já está ótimo. Escolha um qualquer entre (normalmente se escolhe o ponto médio) e FIM.
  • Se não, continue para o Passo 4.

Passo 4: ou ?

  • Se , então escolha como e FIM.
  • Se , escolha como e FIM.
  • Se não, continue para o Passo 5.

Passo 5. , aumentamos uma iteração no contador;

Passo 6. ;

Passo 7. ?

  • Se sim, faça ;
  • Se não, faça .

Passo 8. Volte ao Passo 3

Um bom critério de parada para se adicionar também é um número máximo de iterações. Ele pode ser adicionado Logo depois do Passo 4 por exemplo.

Agora vamos praticar com exercícios?!

Como calcular método da falsa posição?

Algoritmo do Método da Falsa Posição

Exercícios Resolvidos

Exercício Resolvido #1

Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 75, exercício 4 adaptado

Seja f x = - x 3 - cos ⁡ x com zero no intervalo - 1,0 . Use o método da posição falsa para encontrar uma aproximação para a raiz de f com precisão de 10 - 3 .

Passo 1

a 0 , b 0 = - 1,0

ε 1 = ε 2 = 0.001

Iteração 1 :

x 1 = a 0 f b 0 - b 0 f a 0 f b 0 - f a 0 = 1 - 1.4596 = - 0.6851

f x 1 = f - 0.6851 ≅ - 0.4529

f a 0 ∙ f x 1 = 0.4597 ∙ - 0.4529 < 0

Logo, nosso novo intervalo será formado por a 0 e x 1 . Temos então que:

a 1 , b 1 = a 0 , x 1 = - 1 , - 0.6851

Critério de Parada:

b 1 - a 1 = - 0.6851 - - 1 = 0.3149 > 0.001

f a 1 = 0.4597 > 0.001

f b 1 = 0.4529 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 1 , b 1 = - 1 , - 0.6851

ε 1 = ε 2 = 0.001

Iteração 2 :

x 2 = a 1 f b 1 - b 1 f a 1 f b 1 - f a 1 = 0.7678 - 0.9125 = - 0.8414

f x 2 = f - 0.8414 ≅ - 0.0709

f a 1 ∙ f x 2 = 0.4597 ∙ - 0.0709 < 0

Logo, nosso novo intervalo será formado por a 1 e x 2 . Temos então que:

a 2 , b 2 = a 1 , x 2 = - 1 , - 0.8414

Critério de Parada:

b 2 - a 2 = - 0.8414 - - 1 = 0.1586 > 0.0 01

f a 2 = 0.4597 > 0 . 001

f b 2 = 0.0709 > 0.0 01

Como não alcançamos o critério de parada continuamos as iterações.

a 2 , b 2 = - 1 , - 0.8414

ε 1 = ε 2 = 0 . 001

Iteração 3 :

x 3 = a 2 f b 2 - b 2 f a 2 f b 2 - f a 2 = 0.4576 - 0.5306 = - 0.8625

f x 3 = f - 0.8625 ≅ - 0.0088

f a 2 ∙ f x 3 = 0.4597 ∙ - 0.0088 < 0

Logo, nosso novo intervalo será formado por a 2 e x 3 . Temos então que:

a 3 , b 3 = a 2 , x 3 = - 1 , - 0.8625

Critério de Parada:

b 3 - a 3 = - 0.8625 - - 1 = 0.1374 > 0.0 01

f a 3 = 0.4597 > 0 . 001

f b 3 = 0.0088 > 0 . 001

Como não alcançamos o critério de parada continuamos as iterações.

a 3 , b 3 = - 1 , - 0.8625

ε 1 = ε 2 = 0.0 01

Iteração 4 :

x 4 = a 3 f b 3 - b 3 f a 3 f b 3 - f a 3 = 0 . 4053 - 0.4685 = - 0.8651

f x 4 = f - 0.8651 ≅ - 0.0012

f a 3 ∙ f x 4 = 0.4597 ∙ - 0.0010 < 0

Logo, nosso novo intervalo será formado por a 3 e x 4 . Temos então que:

a 4 , b 4 = a 3 , x 4 = - 1 , - 0.8651

Critério de Parada:

b 4 - a 4 = - 0.8651 - - 1 = 0.1349 > 0.0 01

f a 4 = 0.4597 > 0 . 001

f b 4 = 0.0012 > 0.0 01

Como não alcançamos o critério de parada continuamos as iterações.

a 4 , b 4 = - 1 , - 0.8651

ε 1 = ε 2 = 0 . 001

Iteração 5 :

x 5 = a 4 f b 4 - b 4 f a 4 f b 4 - f a 4 = 0.3987 - 0.4608 = - 0.8654

f x 5 = f - 0.8654 ≅ - 0.0001

f a 4 ∙ f x 5 = 0.4597 ∙ - 0.0001 < 0

Logo, nosso novo intervalo será formado por a 4 e x 5 . Temos então que:

a 5 , b 5 = a 4 , x 5 = - 1 , - 0.8654

Critério de Parada:

b 5 - a 5 = - 0.8654 - - 1 = 0.1346 > 0.00001

f a 5 = 0.4597 > 0 . 001

f b 5 = 0.0001 < 0.00 1

Beleza, alcançamos o critério de parada! Então nossa aproximação é x - = - 0.8654 .

Resposta

x - = - 0.8654 .

Exercício Resolvido #2

Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 75, exercício 5d adaptado

Seja f x = x - 0.8 - 0.2 sin ⁡ x com zero no intervalo 0 , π 2 . Use o método da posição falsa para encontrar uma aproximação para a raiz de f com precisão de 10 - 4 .

Passo 1

Beleza, vamos aplicar nosso algoritmo:

a 0 , b 0 = 0 , π 2

ε 1 = ε 2 = 0.0001

Iteração 1 :

x 1 = a 0 f b 0 - b 0 f a 0 f b 0 - f a 0 = 1.25663 1.3708 = 0.91672

f x 1 = f 0.91672 ≅ - 0.042

f a 0 ∙ f x 1 = - 0.8 ∙ - 0.042 > 0

Logo, nosso novo intervalo será formado por x 1 e b 0 . Temos então que:

a 1 , b 1 = x 1 , b 0 = 0.91672 , π 2

Critério de Parada:

b 1 - a 1 = π 2 - 0.91672 = 0.65408 > 0.0001

f a 1 = 0.042 > 0.0001

f b 1 = 0.5708 > 0.0001

Como não alcançamos o critério de parada continuamos as iterações.

a 1 , b 1 = 0.91672 , π 2

ε 1 = ε 2 = 0.0001

Iteração 2 :

x 2 = a 1 f b 1 - b 1 f a 1 f b 1 - f a 1 = 0.58924 0.6128 = 0.96155

f x 2 = f 0.96155 ≅ - 0.00246

f a 1 ∙ f x 2 = - 0.042 ∙ - 0.00246 > 0

Logo, nosso novo intervalo será formado por x 2 e b 1 . Temos então que:

a 2 , b 2 = x 2 , b 1 = 0.96155 , π 2

Critério de Parada:

b 2 - a 2 = π 2 - 0.96155 = 0.60925 > 0.0001

f a 2 = 0.00246 > 0.0001

f b 2 = 0.5708 > 0.0001

Como não alcançamos o critério de parada continuamos as iterações.

a 2 , b 2 = 0.96155 , π 2

ε 1 = ε 2 = 0.0001

Iteração 3 :

x 3 = a 2 f b 2 - b 2 f a 2 f b 2 - f a 2 = 0.55272 0.57326 = 0.96417

f x 3 = f 0.96417 ≅ - 0.00014

f a 2 ∙ f x 3 = - 0.00246 ∙ - 0.00014 > 0

Logo, nosso novo intervalo será formado por x 3 e b 2 . Temos então que:

a 3 , b 3 = x 3 , b 2 = 0.96417 , π 2

Critério de Parada:

b 3 - a 3 = π 2 - 0.96417 = 0.60663 > 0.0001

f a 3 = 0.00014 > 0.0001

f b 3 = 0.5708 > 0.0001

Como não alcançamos o critério de parada continuamos as iterações.

a 3 , b 3 = 0.96417 , π 2

ε 1 = ε 2 = 0 . 0001

Iteração 4 :

x 4 = a 3 f b 3 - b 3 f a 3 f b 3 - f a 3 = 0.55057 0.57094 = 0.96432

f x 4 = f 0.96432 ≅ - 0.000008

f a 3 ∙ f x 4 = - 0.00014 ∙ - 0.000008 > 0

Logo, nosso novo intervalo será formado por x 4 e b 3 . Temos então que:

a 4 , b 4 = x 4 , b 3 = 0.96432 , π 2

Critério de Parada:

b 4 - a 4 = π 2 - 0.96432 = 0.60647 > 0.0 001

f a 4 = 0.000008 = 8 ∙ 10 - 6 < 0.00 01

f b 4 = 0.5708 > 0.00 01

Beleza, ultrapassamos nosso critério de parada! Então uma aproximação para a nossa raiz é x - = 0.96432 .

Resposta

x - = 0.96432 .

Exercício Resolvido #3

Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 75, exercício 6a adaptado

Seja f x = e x + 2 - x + 2 cos ⁡ x - 6 = 0 com zero no intervalo 1,2 . Use o método da posição falsa para encontrar uma aproximação para a raiz de f com precisão de 10 - 4 .

Passo 1

Beleza, vamos aplicar nosso algoritmo:

a 0 , b 0 = 1,2

ε 1 = ε 2 = 0.0001

Iteração 1 :

x 1 = a 0 f b 0 - b 0 f a 0 f b 0 - f a 0 = 4.2089 9 2.50788 = 1.67831

f x 1 = f 1.67831 ≅ - 0.54567

f a 0 ∙ f x 1 = - 1.70111 ∙ - 0.54567 > 0

Logo, nosso novo intervalo será formado por x 1 e b 0 . Temos então que:

a 1 , b 1 = x 1 , b 0 = 1.67831 , 2

Critério de Parada:

b 1 - a 1 = 2 - 1.67831 = 0.32169 > 0.0001

f a 1 = 0.54567 > 0.0001

f b 1 = 0.80676 > 0.0001

Como não alcançamos o critério de parada continuamos as iterações.

a 1 , b 1 = 1.67831 , 2

ε 1 = ε 2 = 0.0001

Iteração 2 :

x 2 = a 1 f b 1 - b 1 f a 1 f b 1 - f a 1 = 2.44534 1.35244 = 1.8081

f x 2 = f 1.8081 ≅ - 0.08574

f a 1 ∙ f x 2 = - 0.54567 ∙ - 0.08574 > 0

Logo, nosso novo intervalo será formado por x 2 e b 1 . Temos então que:

a 2 , b 2 = x 2 , b 1 = 1.8081 , 2

Critério de Parada:

b 2 - a 2 = 2 - 1.8081 = 0.1919 > 0.0001

f a 2 = 0.0857 4 > 0.0001

f b 2 = 0.80676 > 0.0001

Como não alcançamos o critério de parada continuamos as iterações.

a 2 , b 2 = 1.8081 , 2

ε 1 = ε 2 = 0.0001

Iteração 3 :

x 3 = a 2 f b 2 - b 2 f a 2 f b 2 - f a 2 = 1.63019 0.8925 = 1.82654

f x 3 = f 1.82654 ≅ - 0.01165

f a 2 ∙ f x 3 = - 0.08574 ∙ - 0.01165 > 0

Logo, nosso novo intervalo será formado por x 3 e b 2 . Temos então que:

a 3 , b 3 = x 3 , b 2 = 1.82654 , 2

Critério de Parada:

b 3 - a 3 = 2 - 1.82654 = 0.17346 > 0.0001

f a 3 = 0.01165 > 0.0001

f b 3 = 0.80676 > 0.0001

Como não alcançamos o critério de parada continuamos as iterações.

a 3 , b 3 = 1.82654 , 2

ε 1 = ε 2 = 0.0001

Iteração 4 :

x 4 = a 3 f b 3 - b 3 f a 3 f b 3 - f a 3 = 1.82901

f x 4 = f 1.82901 ≅ - 0.00155

f a 3 ∙ f x 4 = - 0.01165 ∙ - 0.00155 > 0

Logo, nosso novo intervalo será formado por x 4 e b 3 . Temos então que:

a 4 , b 4 = x 4 , b 3 = 1.82901 , 2

Critério de Parada:

b 4 - a 4 = 2 - 1.82901 = 0.17099 > 0.0001

f a 4 = 0.00155 > 0.0001

f b 4 = 0.80676 > 0.0001

Como não alcançamos o critério de parada continuamos as iterações.

a 4 , b 4 = 1.82901 , 2

ε 1 = ε 2 = 0.0 001

Iteração 5 :

x 5 = a 4 f b 4 - b 4 f a 4 f b 4 - f a 4 = 1.82933

f x 5 = f 1.82933 ≅ - 0.00021

f a 4 ∙ f x 5 = - 0.00155 ∙ - 0.00021 > 0

Logo, nosso novo intervalo será formado por x 5 e b 4 . Temos então que:

a 5 , b 5 = x 5 , b 4 = 1.82933 , 2

Critério de Parada:

b 5 - a 5 = 2 - 1.82933 = 0.17067 > 0.0 001

f a 5 = 0.00021 > 0.00 01

f b 5 = 0.80676 > 0.0 001

Como não alcançamos o critério de parada continuamos as iterações.

a 5 , b 5 = 1.82933 , 2

ε 1 = ε 2 = 0.0 001

Iteração 6 :

x 6 = a 5 f b 5 - b 5 f a 5 f b 5 - f a 5 = 1.82938

f x 6 = f 1.82938 ≅ - 0.0 0003

f a 5 ∙ f x 6 = - 0.00021 ∙ - 0.00003 > 0

Logo, nosso novo intervalo será formado por x 6 e b 5 . Temos então que:

a 6 , b 6 = x 6 , b 5 = 1.82938 , 2

Critério de Parada:

b 6 - a 6 = 2 - 1.82938 = 0.17062 > 0.000 1

f a 6 = 0.00003 < 0.0 001

f b 6 = 0.80676 > 0.00 01

Beleza, ultrapassamos nosso critério de parada! Então uma aproximação para a nossa raiz é x - = 1.82938 .

Resposta

x - = 1.82938 .

Exercício Resolvido #4

Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 75, exercício 6b adaptado

Seja f x = ln ⁡ x - 1 + cos ⁡ x - 1 = 0 com zero no intervalo 1.3,2 . Use o método da posição falsa para encontrar uma aproximação para a raiz de f com precisão de 10 - 4 .

Passo 1

Beleza, vamos aplicar nosso algoritmo:

a 0 , b 0 = 1.3,2

ε 1 = ε 2 = 0.0001

Iteração 1 :

x 1 = a 0 f b 0 - b 0 f a 0 f b 0 - f a 0 = 1.52061

f x 1 = f 1.52061 ≅ 0.21476

f a 0 ∙ f x 1 = - 0.24864 ∙ 0.21476 < 0

Logo, nosso novo intervalo será formado por a 0 e x 1 . Temos então que:

a 1 , b 1 = a 0 , x 1 = 1.3,1.52061

Critério de Parada:

b 1 - a 1 = 0.22061 > 0.0001

f a 1 = 0.24864 > 0.0001

f b 1 = 0.21476 > 0.0001

Como não alcançamos o critério de parada continuamos as iterações.

a 1 , b 1 = 1.3,1.52061

ε 1 = ε 2 = 0.0001

Iteração 2 :

x 2 = a 1 f b 1 - b 1 f a 1 f b 1 - f a 1 = 1.41837

f x 2 = f 1.41837 ≅ 0.04236

f a 1 ∙ f x 2 = - 0.24864 ∙ 0.04236 < 0

Logo, nosso novo intervalo será formado por a 1 e x 2 . Temos então que:

a 2 , b 2 = a 1 , x 2 = 1.3,1.41837

Critério de Parada:

b 2 - a 2 = 0.11837 > 0.0001

f a 2 = 0.24864 > 0.0001

f b 2 = 0.04236 > 0.0001

Como não alcançamos o critério de parada continuamos as iterações.

a 2 , b 2 = 1.3,1.41837

ε 1 = ε 2 = 0.0001

Iteração 3 :

x 3 = a 2 f b 2 - b 2 f a 2 f b 2 - f a 2 = 1.40114

f x 3 = f 1.40114 ≅ 0.00717

f a 2 ∙ f x 3 = - 0.24864 ∙ 0.00716 < 0

Logo, nosso novo intervalo será formado por a 2 e x 3 . Temos então que:

a 3 , b 3 = a 2 , x 3 = 1.3,1.40114

Critério de Parada:

b 3 - a 3 = 0.10114 > 0.0001

f a 3 = 0.24864 > 0.0001

f b 3 = 0.00716 > 0.0001

Como não alcançamos o critério de parada continuamos as iterações.

a 3 , b 3 = 1.3,1.40114

ε 1 = ε 2 = 0.0001

Iteração 4 :

x 4 = a 3 f b 3 - b 3 f a 3 f b 3 - f a 3 = 1.3983

f x 4 = f 1.3983 ≅ 0.00118

f a 3 ∙ f x 4 = - 0.24864 ∙ 0.00118 < 0

Logo, nosso novo intervalo será formado por a 3 e x 4 . Temos então que:

a 4 , b 4 = a 3 , x 4 = 1.3 , 1.3983

Critério de Parada:

b 4 - a 4 = 0.0983 > 0.0001

f a 4 = 0.24864 > 0.0001

f b 4 = 0.00118 > 0.0001

Como não alcançamos o critério de parada continuamos as iterações.

a 4 , b 4 = 1.3 , 1.3983

ε 1 = ε 2 = 0.0001

Iteração 5 :

x 5 = a 4 f b 4 - b 4 f a 4 f b 4 - f a 4 = 1.39784

f x 5 = f 1.39784 ≅ 0.00019

f a 4 ∙ f x 5 = - 0.24864 ∙ 0.00019 < 0

Logo, nosso novo intervalo será formado por a 4 e x 5 . Temos então que:

a 5 , b 5 = a 4 , x 5 = 1.3,1.39784

Critério de Parada:

b 5 - a 5 = 0.09784 > 0.0001

f a 5 = 0.24864 > 0.0001

f b 5 = 0.00019 > 0.0001

Como não alcançamos o critério de parada continuamos as iterações.

a 5 , b 5 = 1.3,1.39784

ε 1 = ε 2 = 0.0001

Iteração 6 :

x 6 = a 5 f b 5 - b 5 f a 5 f b 5 - f a 5 = 1.39776

f x 6 = f 1.39776 ≅ 0.0000 3

f a 5 ∙ f x 6 = - 0 . 24864 ∙ 0.00003 < 0

Logo, nosso novo intervalo será formado por a 5 e x 6 . Temos então que:

a 6 , b 6 = a 5 , x 6 = 1.3 , 1.39776

Critério de Parada:

b 6 - a 6 = 0.09776 > 0.0001

f a 6 = 0.24864 > 0.0001

f b 6 = 0.00003 < 0.0001

Beleza, ultrapassamos nosso critério de parada! Então uma aproximação para a nossa raiz é x - = 1.39776 .

Resposta

x - = 1.39776 .

Exercício Resolvido #5

Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 75, exercício 6c adaptado

Seja f x = 2 x c o s 2 x - x - 2 2 com zero no intervalo 2,3 . Use o método da posição falsa para encontrar uma aproximação para a raiz de f com precisão de 10 - 5 .

Passo 1

a 0 , b 0 = 2,3

ε 1 = ε 2 = 0.000 0 1

Iteração 1 :

x 1 = a 0 f b 0 - b 0 f a 0 f b 0 - f a 0 = 2.35449

f x 1 = f 2.35449 ≅ - 0.141717

f a 0 ∙ f x 1 = - 2.614574 ∙ - 0.141716 > 0

Logo, nosso novo intervalo será formado por x 1 e b 0 . Temos então que:

a 1 , b 1 = x 1 , b 0 = 2.35449,3

Critério de Parada:

b 1 - a 1 = 0.64551 > 0.0 0 001

f a 1 = 0.141717 > 0.0 0 001

f b 1 = 4.761022 > 0.0 0 001

Como não alcançamos o critério de parada continuamos as iterações.

a 1 , b 1 = 2.35449,3

ε 1 = ε 2 = 0.0 0 001

Iteração 2 :

x 2 = a 1 f b 1 - b 1 f a 1 f b 1 - f a 1 = 2.373149

f x 2 = f 2.373149 ≅ 0.021669

f a 1 ∙ f x 2 = - 0.141717 ∙ 0.021669 < 0

Logo, nosso novo intervalo será formado por a 1 e x 2 . Temos então que:

a 2 , b 2 = a 1 , x 2 = 2.35449 , 2.373149

Critério de Parada:

b 2 - a 2 = 0.018659 > 0.00 0 01

f a 2 = 0.141717 > 0.00 0 01

f b 2 = 0.021669 > 0.0 0 001

Como não alcançamos o critério de parada continuamos as iterações.

a 2 , b 2 = 2.35449,2.373149

ε 1 = ε 2 = 0.00 0 01

Iteração 3 :

x 3 = a 2 f b 2 - b 2 f a 2 f b 2 - f a 2 = 2.370674

f x 3 = f 2.370674 ≅ - 0.000113

f a 2 ∙ f x 3 = - 0.141717 ∙ - 0.000113 > 0

Logo, nosso novo intervalo será formado por x 3 e b 2 . Temos então que:

a 3 , b 3 = x 3 , b 2 = 2.370674 , 2.373149

Critério de Parada:

b 3 - a 3 = 0.002475 > 0.0 0 001

f a 3 = 0.000113 > 0.00 0 01

f b 3 = 0.021669 > 0.0 0 001

Como não alcançamos o critério de parada continuamos as iterações.

a 3 , b 3 = 2.370674 , 2.373149

ε 1 = ε 2 = 0.00 0 01

Iteração 4 :

x 4 = a 3 f b 3 - b 3 f a 3 f b 3 - f a 3 = 2.370686

f x 4 = f 2.370686 ≅ - 8 ∙ 10 - 8

f a 3 ∙ f x 4 = - 0.000113 ∙ - 8 ∙ 10 - 8 > 0

Logo, nosso novo intervalo será formado por x 4 e b 3 . Temos então que:

a 4 , b 4 = x 4 , b 3 = 2.370686 , 2.373149

Critério de Parada:

b 4 - a 4 = 0.002462 > 0.0 0 001

f a 4 = 8 ∙ 10 - 8 < 0.0 0 001

f b 4 = 0.021669 > 0.0 0 001

Beleza, ultrapassamos nosso critério de parada! Essa até que foi rápida. Então uma aproximação para a nossa raiz é x - = 2.370686 .

Resposta

x - = 2.370686 .

Exercício Resolvido #6

Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 75, exercício 6f adaptado

Seja f x = sin ⁡ x - e - x com zeros nos intervalos 3,4 e 6,7 . Use o método da posição falsa para encontrar uma aproximação para as raízes de f com precisão de 10 - 5 .

Passo 1

Vamos começar com 3,4 :

a 0 , b 0 = 3,4

ε 1 = ε 2 = 0.0 0 001

Iteração 1 :

x 1 = a 0 f b 0 - b 0 f a 0 f b 0 - f a 0 = 3.10541

f x 1 = f 3.10541 ≅ - 0.008632

f a 0 ∙ f x 1 = 0.091333 ∙ - 0.008632 < 0

Logo, nosso novo intervalo será formado por a 0 e x 1 . Temos então que:

a 1 , b 1 = a 0 , x 1 = 3 , 3.10541

Critério de Parada:

b 1 - a 1 = 0.10541 > 0.00 0 01

f a 1 = 0.091333 > 0.0 0 001

f b 1 = 0.008 632 > 0.0 0 001

Como não alcançamos o critério de parada continuamos as iterações.

a 1 , b 1 = 3,3.10541

ε 1 = ε 2 = 0.0 0 001

Iteração 2 :

x 2 = a 1 f b 1 - b 1 f a 1 f b 1 - f a 1 = 3.096308

f x 2 = f 3.096308 ≅ 0.00005

f a 1 ∙ f x 2 = 0.091333 ∙ 0.00005 > 0

Logo, nosso novo intervalo será formado por x 2 e b 1 . Temos então que:

a 2 , b 2 = x 2 , b 1 = 3.096308 , 3.10541

Critério de Parada:

b 2 - a 2 = 0.009102 > 0.00 0 01

f a 2 = 0.00005 > 0.0 0 001

f b 2 = 0.008632 > 0.00 0 01

Como não alcançamos o critério de parada continuamos as iterações.

a 2 , b 2 = 3.096308 , 3.10541

ε 1 = ε 2 = 0.00 0 01

Iteração 3 :

x 3 = a 2 f b 2 - b 2 f a 2 f b 2 - f a 2 = 3.096364

f x 3 = f 3.096364 ≅ 2 ∙ 10 - 8

f a 2 ∙ f x 3 = 5 ∙ 10 - 5 ∙ 2 ∙ 10 - 8 > 0

Logo, nosso novo intervalo será formado por x 3 e b 2 . Temos então que:

a 3 , b 3 = x 3 , b 2 = 3.096364 , 3.10541

Critério de Parada:

b 3 - a 3 = 0.009046 > 0.0 0 001

f a 3 = 2 ∙ 10 - 8 < 0.00 0 01

f b 3 = 0.008632 > 0.0 0 001

Opa, chegamos na precisão que queríamos! Então uma aproximação para a nossa raiz é x - = 3.096364 .

Passo 2

Próximo intervalo agora:

a 0 , b 0 = 6,7

ε 1 = ε 2 = 0.00001

Iteração 1 :

x 1 = a 0 f b 0 - b 0 f a 0 f b 0 - f a 0 = 6.300537

f x 1 = f 6.300536 ≅ 0.015515

f a 0 ∙ f x 1 = - 0.281894 ∙ 0.015515 < 0

Logo, nosso novo intervalo será formado por a 0 e x 1 . Temos então que:

a 1 , b 1 = a 0 , x 1 = 6 , 6.300537

Critério de Parada:

b 1 - a 1 = 0.300537 > 0.00001

f a 1 = 0.281894 > 0.00001

f b 1 = 0.015515 > 0.00001

Como não alcançamos o critério de parada continuamos as iterações.

a 1 , b 1 = 6,6.300537

ε 1 = ε 2 = 0.00001

Iteração 2 :

x 2 = a 1 f b 1 - b 1 f a 1 f b 1 - f a 1 = 6.284858

f x 2 = f 6.284858 ≅ - 0.000191

f a 1 ∙ f x 2 = - 0.281894 ∙ - 0.000191 > 0

Logo, nosso novo intervalo será formado por x 2 e b 1 . Temos então que:

a 2 , b 2 = x 2 , b 1 = 6.284858 , 6.300537

Critério de Parada:

b 2 - a 2 = 0.015679 > 0.00001

f a 2 = 0.000191 > 0.00001

f b 2 = 0.015515 > 0.00001

Como não alcançamos o critério de parada continuamos as iterações.

a 2 , b 2 = 6.284858 , 6.300537

ε 1 = ε 2 = 0.00001

Iteração 3 :

x 3 = a 2 f b 2 - b 2 f a 2 f b 2 - f a 2 = 6.285049

f x 3 = f 6.285049 ≅ 1 ∙ 10 - 8

f a 2 ∙ f x 3 = - 0.000191 ∙ 1 ∙ 10 - 8 < 0

Logo, nosso novo intervalo será formado por a 2 e x 3 . Temos então que:

a 3 , b 3 = a 2 , x 3 = 6.284858 , 6.285049

Critério de Parada:

b 3 - a 3 = 0.000191 > 0.00001

f a 3 = 0.000191 < 0.00001

f b 3 = 1 ∙ 10 - 8 < 0.00001

Fim de papo! Quem dera sempre fosse tão rápido né? Só três iterações haha. Então uma aproximação para a nossa raiz é x - = 6.285049 .

Resposta

x - = 3.096364 e x - = 6.285049 .

Exercício Resolvido #7

Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 75, exercício 5b adaptado

Seja f x = x 3 + 3 x 2 - 1 com um zero no intervalo - 3 , - 2 . Calcule a raiz de f x com precisão de ε = 10 - 5 utilizando o método da posição falsa.

Passo 1

a 0 , b 0 = - 3 , - 2

ε 1 = ε 2 = 0.00001

Iteração 1 :

x 1 = a 0 f b 0 - b 0 f a 0 f b 0 - f a 0 = - 2.75

f x 1 = f - 2.75 ≅ 0.890625

f a 0 ∙ f x 1 = - 1 ∙ 0.890625 < 0

Logo, nosso novo intervalo será formado por a 0 e x 1 . Temos então que:

a 1 , b 1 = a 0 , x 1 = - 3 , - 2.75

Critério de Parada:

b 1 - a 1 = 0.25 > 0.00001

f a 1 = 1 > 0.00001

f b 1 = 0.890625 > 0.00001

Como não alcançamos o critério de parada continuamos as iterações.

a 1 , b 1 = - 3 , - 2.75

ε 1 = ε 2 = 0.00001

Iteração 2 :

x 2 = a 1 f b 1 - b 1 f a 1 f b 1 - f a 1 = - 2.867769

f x 2 = f - 2.867769 ≅ 0.087484

f a 1 ∙ f x 2 = - 1 ∙ 0.087484 < 0

Logo, nosso novo intervalo será formado por a 1 e x 2 . Temos então que:

a 2 , b 2 = a 1 , x 2 = - 3 , - 2.867769

Critério de Parada:

b 2 - a 2 = 0.132231 > 0.00001

f a 2 = 1 > 0.00001

f b 2 = 0.087484 > 0.00001

Como não alcançamos o critério de parada continuamos as iterações.

a 2 , b 2 = - 3 , - 2.867769

ε 1 = ε 2 = 0.00001

Iteração 3 :

x 3 = a 2 f b 2 - b 2 f a 2 f b 2 - f a 2 = - 2.878406

f x 3 = f - 2.878406 ≅ 0.007432

f a 2 ∙ f x 3 = - 1 ∙ 0.007432 < 0

Logo, nosso novo intervalo será formado por a 2 e x 3 . Temos então que:

a 3 , b 3 = a 2 , x 3 = - 3 , - 2.878406

Critério de Parada:

b 3 - a 3 = 0.121594 > 0.00001

f a 3 = 1 > 0.00001

f b 3 = 0.007432 > 0.00001

Como não alcançamos o critério de parada continuamos as iterações.

a 3 , b 3 = - 3 , - 2.878406

ε 1 = ε 2 = 0.00001

Iteração 4 :

x 4 = a 3 f b 3 - b 3 f a 3 f b 3 - f a 3 = - 2.879303

f x 4 = f - 2.879303 ≅ 0.000623

f a 3 ∙ f x 4 = - 1 ∙ 0.000623 < 0

Logo, nosso novo intervalo será formado por a 3 e x 4 . Temos então que:

a 4 , b 4 = a 3 , x 4 = - 3 , - 2.879303

Critério de Parada:

b 4 - a 4 = 0.120697 > 0.00001

f a 4 = 1 > 0.00001

f b 4 = 0.000623 > 0.00001

Como não alcançamos o critério de parada continuamos as iterações.

a 4 , b 4 = - 3 , - 2.879303

ε 1 = ε 2 = 0.00001

Iteração 5 :

x 5 = a 4 f b 4 - b 4 f a 4 f b 4 - f a 4 = - 2.879378

f x 5 = f - 2.879378 ≅ 5.2 ∙ 10 - 5

f a 4 ∙ f x 5 = - 1 ∙ 5.2 ∙ 10 - 5 < 0

Logo, nosso novo intervalo será formado por a 4 e x 5 . Temos então que:

a 5 , b 5 = a 4 , x 5 = - 3 , - 2.879378

Critério de Parada:

b 5 - a 5 = 0.120622 > 0.00001

f a 5 = 1 > 0.00001

f b 5 = 5.2 ∙ 10 - 5 > 0.00001

Como não alcançamos o critério de parada continuamos as iterações.

a 5 , b 5 = - 3 , - 2.879378

ε 1 = ε 2 = 0.00001

Iteração 6 :

x 6 = a 5 f b 5 - b 5 f a 5 f b 5 - f a 5 = - 2.879385

f x 6 = f - 2.879385 ≅ 4 ∙ 10 - 6

f a 5 ∙ f x 6 = - 1 ∙ 4 ∙ 10 - 6 < 0

Logo, nosso novo intervalo será formado por a 5 e x 6 . Temos então que:

a 6 , b 6 = a 5 , x 6 = - 3 , - 2.879385

Critério de Parada:

b 6 - a 6 = 0.120615 > 0.00001

f a 6 = 1 > 0.00001

f b 6 = 4 ∙ 10 - 6 < 0.00001

Pronto, chegamos na aproximação com a precisão pedida. A raiz é então, com precisão de 10 - 5 , x - = - 2.879385 .

Resposta

x - = - 2.879385 .

Exercício Resolvido #8

Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 76, exercício 12a adaptado

Seja f x = x 2 - 4 x + 4 - ln ⁡ x com um zero no intervalo 1 , 2 . Calcule a raiz de f x com precisão de ε = 10 - 4 utilizando o método da posição falsa.

Passo 1

a 0 , b 0 = 1,2

ε 1 = ε 2 = 0.0001

Iteração 1 :

x 1 = a 0 f b 0 - b 0 f a 0 f b 0 - f a 0 = 1.59062

f x 1 = f 1.59062 ≅ - 0.29653

f a 0 ∙ f x 1 = 1 ∙ - 0.29653 < 0

Logo, nosso novo intervalo será formado por a 0 e x 1 . Temos então que:

a 1 , b 1 = a 0 , x 1 = 1,1.59062

Critério de Parada:

b 1 - a 1 = 0.59062 > 0.0001

f a 1 = 1 > 0.0001

f b 1 = 0.29653 > 0.0001

Como não alcançamos o critério de parada continuamos as iterações.

a 1 , b 1 = 1,1.59062

ε 1 = ε 2 = 0.0001

Iteração 2 :

x 2 = a 1 f b 1 - b 1 f a 1 f b 1 - f a 1 = 1.45554

f x 2 = f 1.45554 ≅ - 0.07894

f a 1 ∙ f x 2 = 1 ∙ - 0.07894 < 0

Logo, nosso novo intervalo será formado por a 1 e x 2 . Temos então que:

a 2 , b 2 = a 1 , x 2 = 1,1.45554

Critério de Parada:

b 2 - a 2 = 0.45554 > 0.0001

f a 2 = 1 > 0.0001

f b 2 = 0.07894 > 0.0001

Como não alcançamos o critério de parada continuamos as iterações.

a 2 , b 2 = 1,1.45554

ε 1 = ε 2 = 0.0001

Iteração 3 :

x 3 = a 2 f b 2 - b 2 f a 2 f b 2 - f a 2 = 1.42221

f x 3 = f 1.42221 ≅ - 0.01837

f a 2 ∙ f x 3 = 1 ∙ - 0.01837 < 0

Logo, nosso novo intervalo será formado por a 2 e x 3 . Temos então que:

a 3 , b 3 = a 2 , x 3 = 1,1.42221

Critério de Parada:

b 3 - a 3 = 0 . 42221 > 0.0001

f a 3 = 1 > 0.0001

f b 3 = 0.01837 > 0.0001

Como não alcançamos o critério de parada continuamos as iterações.

a 3 , b 3 = 1,1.42221

ε 1 = ε 2 = 0.0001

Iteração 4 :

x 4 = a 3 f b 3 - b 3 f a 3 f b 3 - f a 3 = 1.41459

f x 4 = f 1.41459 ≅ - 0.00414

f a 3 ∙ f x 4 = 1 ∙ - 0.00414 < 0

Logo, nosso novo intervalo será formado por a 3 e x 4 . Temos então que:

a 4 , b 4 = a 3 , x 4 = 1 , 1.41459

Critério de Parada:

b 4 - a 4 = 0 . 41459 > 0.0001

f a 4 = 1 > 0.0001

f b 4 = 0.00414 > 0.0001

Como não alcançamos o critério de parada continuamos as iterações.

a 4 , b 4 = 1 , 1.41459

ε 1 = ε 2 = 0.0001

Iteração 5 :

x 5 = a 4 f b 4 - b 4 f a 4 f b 4 - f a 4 = 1.41288

f x 5 = f 1.41288 ≅ - 0.00093

f a 4 ∙ f x 5 = 1 ∙ - 0.00093 < 0

Logo, nosso novo intervalo será formado por a 4 e x 5 . Temos então que:

a 5 , b 5 = a 4 , x 5 = 1 , 1.41288

Critério de Parada:

b 5 - a 5 = 0 . 41288 > 0.0001

f a 5 = 1 > 0.0001

f b 5 = 0.00093 > 0.0001

Como não alcançamos o critério de parada continuamos as iterações.

a 5 , b 5 = 1 , 1.41288

ε 1 = ε 2 = 0.0001

Iteração 6 :

x 6 = a 5 f b 5 - b 5 f a 5 f b 5 - f a 5 = 1.4125

f x 6 = f 1.4125 ≅ - 0.00021

f a 5 ∙ f x 6 = 1 ∙ - 0.00021 < 0

Logo, nosso novo intervalo será formado por a 5 e x 6 . Temos então que:

a 6 , b 6 = a 5 , x 6 = 1 , 1.4125

Critério de Parada:

b 6 - a 6 = 0 . 4125 > 0.0001

f a 6 = 1 > 0.0001

f b 6 = 0.00021 > 0.0001

Como não alcançamos o critério de parada continuamos as iterações.

a 6 , b 6 = 1 , 1.4125

ε 1 = ε 2 = 0.0001

Iteração 7 :

x 7 = a 6 f b 6 - b 6 f a 6 f b 6 - f a 6 = 1.41242

f x 7 = f 1.41242 ≅ - 4 ∙ 10 - 5

f a 6 ∙ f x 7 = 1 ∙ - 4 ∙ 10 - 5 < 0

Logo, nosso novo intervalo será formado por a 5 e x 6 . Temos então que:

a 7 , b 7 = a 6 , x 7 = 1 , 1.41242

Critério de Parada:

b 7 - a 7 = 0 . 41242 > 0.0001

f a 7 = 1 > 0.0001

f b 7 = 4 ∙ 10 - 5 < 0.0001

Aê, chegamos no critério de parada! Então uma aproximação para a nossa raiz é x - = 1.41242 .

Resposta

x - = 1.41242 .

Exercício Resolvido #9

Elaboração Própria

Encontre uma aproximação para 6 com precisão de 10 - 4 utilizando o método da posição falsa.

Passo 1

Beleza, aqui nós temos que pensar um pouco, não é só sair jogando o algoritmo. Sempre que tiver algo desse tipo você vai querer se livrar da raiz (ninguém gosta dessa bagaça). Então você faz o seguinte:

6 2 = 6

6 2 - 6 = 0

E como você quer encontrar uma aproximação para a raiz de seis é só substituir ela pelo x :

x 2 - 6 = 0

Opa, agora já ta parecendo algo que a gente possa usar né? Falta só um intervalo que contenha a raiz. 6 está entre 4 e 9 concorda? Então sabemos que ele está no intervalo 2,3 . E de fato,

f 2 ∙ f 3 = - 2 ∙ 3 < 0

Logo, podemos usar o método da posição falsa! Agora é só jogar no algoritmo e partir pro abraço ;)

Passo 2

a 0 , b 0 = 2,3

ε 1 = ε 2 = 0.0001

Iteração 1 :

x 1 = a 0 f b 0 - b 0 f a 0 f b 0 - f a 0 = 2.4

f x 1 = f 2.4 ≅ - 0.24

f a 0 ∙ f x 1 = - 2 ∙ - 0.24 > 0

Logo, nosso novo intervalo será formado por x 1 e b 0 . Temos então que:

a 1 , b 1 = x 1 , b 0 = 2.4,3

Critério de Parada:

b 1 - a 1 = 0.6 > 0.0001

f a 1 = 0.24 > 0.0001

f b 1 = 3 > 0.0001

Como não alcançamos o critério de parada continuamos as iterações.

a 1 , b 1 = 2.4,3

ε 1 = ε 2 = 0.0001

Iteração 2 :

x 2 = a 1 f b 1 - b 1 f a 1 f b 1 - f a 1 = 2.44444

f x 2 = f 2.44444 ≅ - 0.02469

f a 1 ∙ f x 2 = - 0.24 ∙ - 0.02469 > 0

Logo, nosso novo intervalo será formado por x 2 e b 1 . Temos então que:

a 2 , b 2 = x 2 , b 1 = 2.44444 , 3

Critério de Parada:

b 2 - a 2 = 0.55556 > 0.0001

f a 2 = 0.02469 > 0.0001

f b 2 = 3 > 0.0001

Como não alcançamos o critério de parada continuamos as iterações.

a 2 , b 2 = 2.44444 , 3

ε 1 = ε 2 = 0.0001

Iteração 3 :

x 3 = a 2 f b 2 - b 2 f a 2 f b 2 - f a 2 = 2.44898

f x 3 = f 2.44898 ≅ - 0.0025

f a 2 ∙ f x 3 = - 0.02469 ∙ - 0.002 5 > 0

Logo, nosso novo intervalo será formado por x 3 e b 2 . Temos então que:

a 3 , b 3 = x 3 , b 2 = 2.44898 , 3

Critério de Parada:

b 3 - a 3 = 0.55102 > 0.0001

f a 3 = 0.0025 > 0.0001

f b 3 = 3 > 0.0001

Como não alcançamos o critério de parada continuamos as iterações.

a 3 , b 3 = 2.44898,3

ε 1 = ε 2 = 0.0001

Iteração 4 :

x 4 = a 3 f b 3 - b 3 f a 3 f b 3 - f a 3 = 2.44944

f x 4 = f 2.44944 ≅ - 0.00025

f a 3 ∙ f x 4 = - 0.0025 ∙ - 0.00025 > 0

Logo, nosso novo intervalo será formado por x 4 e b 3 . Temos então que:

a 4 , b 4 = x 4 , b 3 = 2.44944 , 3

Critério de Parada:

b 4 - a 4 = 0.55056 > 0.0001

f a 4 = 0.00025 > 0.0001

f b 4 = 3 > 0.0001

Como não alcançamos o critério de parada continuamos as iterações.

a 4 , b 4 = 2.44944,3

ε 1 = ε 2 = 0.0001

Iteração 5 :

x 5 = a 4 f b 4 - b 4 f a 4 f b 4 - f a 4 = 2.44948

f x 5 = f 2.44948 ≅ - 2 ∙ 10 - 5

f a 4 ∙ f x 5 = - 0.00025 ∙ - 2 ∙ 10 - 5 > 0

Logo, nosso novo intervalo será formado por x 5 e b 4 . Temos então que:

a 5 , b 5 = x 5 , b 4 = 2.44948 , 3

Critério de Parada:

b 5 - a 5 = 0.55052 > 0.0001

f a 5 = 2 ∙ 10 - 5 < 0.0001

f b 5 = 3 > 0.0001

E chegamos na nossa aproximação para 6 . x - = 2.44948 .

Resposta

x - = 2.44948 .

Exercício Resolvido #10

Elaboração Própria

Seja f x = x + ln ⁡ x com um zero no intervalo 0.2,2 . Calcule a raiz de f x com precisão de ε = 10 - 5 utilizando o método da posição falsa.

Passo 1

a 0 , b 0 = 0.2,2

ε 1 = ε 2 = 0.00001

Iteração 1 :

x 1 = a 0 f b 0 - b 0 f a 0 f b 0 - f a 0 = 3.357505 4.102585 = 0.818388

f x 1 = f 0.818388 ≅ 0.618

f a 0 ∙ f x 1 = - 1.41 ∙ 0.618 < 0

Logo, nosso novo intervalo será formado por a 0 e x 1 . Temos então que:

a 1 , b 1 = a 0 , x 1 = 0.2,0.818388

Critério de Parada:

b 1 - a 1 = 0.818388 - 0.2 = 0.618388 > 0.00001

f a 1 = 1.409438 > 0.00001

f b 1 = 0.617969 > 0.00001

Como não alcançamos o critério de parada continuamos as iterações.

a 1 , b 1 = 0.2,0.818388

ε 1 = ε 2 = 0.00001

Iteração 2 :

x 2 = a 1 f b 1 - b 1 f a 1 f b 1 - f a 1 = 1.27706 2.027407 = 0.629899

f x 2 = f 0.629899 ≅ 0.168

f a 1 ∙ f x 2 = - 1.41 ∙ 0.168 < 0

Logo, nosso novo intervalo será formado por a 1 e x 2 . Temos então que:

a 2 , b 2 = a 1 , x 2 = 0.2,0.629899

Critério de Parada:

b 2 - a 2 = 0.629899 - 0.2 = 0.429899 > 0.00001

f a 2 = 1.409438 > 0.00001

f b 2 = 0.167702 > 0.00001

Como não alcançamos o critério de parada continuamos as iterações.

a 2 , b 2 = 0.2,0.629899

ε 1 = ε 2 = 0.00001

Iteração 3 :

x 3 = a 2 f b 2 - b 2 f a 2 f b 2 - f a 2 = 0.921343 1.57714 = 0.584186

f x 3 = f 0.584186 ≅ 0.047

f a 2 ∙ f x 3 = - 1.41 ∙ 0.047 < 0

Logo, nosso novo intervalo será formado por a 2 e x 3 . Temos então que:

a 3 , b 3 = a 2 , x 3 = 0.2,0.584186

Critério de Parada:

b 3 - a 3 = 0.584186 - 0.2 = 0.384186 > 0.00001

f a 3 = 1.409438 > 0.00001

f b 3 = 0.046650 > 0.00001

Como não alcançamos o critério de parada continuamos as iterações.

a 3 , b 3 = 0.2,0.584186

ε 1 = ε 2 = 0.00001

Iteração 4 :

x 4 = a 3 f b 3 - b 3 f a 3 f b 3 - f a 3 = 0.832704 1.456088 = 0.571877

f x 4 = f 0.571877 ≅ 0.013

f a 3 ∙ f x 4 = - 1.41 ∙ 0.013 < 0

Logo, nosso novo intervalo será formado por a 3 e x 4 . Temos então que:

a 4 , b 4 = a 3 , x 4 = 0.2,0.571877

Critério de Parada:

b 4 - a 4 = 0.571877 - 0.2 = 0.371877 > 0.00001

f a 4 = 1.409438 > 0.00001

f b 4 = 0.013047 > 0.00001

Como não alcançamos o critério de parada continuamos as iterações.

a 4 , b 4 = 0.2,0.571877

ε 1 = ε 2 = 0.00001

Iteração 5 :

x 5 = a 4 f b 4 - b 4 f a 4 f b 4 - f a 4 = 0.808635 1.422485 = 0.568466

f x 5 = f 0.568466 ≅ 0.004

f a 4 ∙ f x 5 = - 1.41 ∙ 0.004 < 0

Logo, nosso novo intervalo será formado por a 4 e x 5 . Temos então que:

a 5 , b 5 = a 4 , x 5 = 0.2,0.568466

Critério de Parada:

b 5 - a 5 = 0.568466 - 0.2 = 0.368466 > 0.00001

f a 5 = 1.409438 > 0.00001

f b 5 = 0.003655 > 0.00001

Como não alcançamos o critério de parada continuamos as iterações.

a 5 , b 5 = 0.2,0.568466

ε 1 = ε 2 = 0.00001

Iteração 6 :

x 6 = a 5 f b 5 - b 5 f a 5 f b 5 - f a 5 = 0.801949 1.413092 = 0.567514

f x 6 = f 0.567514 ≅ 0.001

f a 5 ∙ f x 6 = - 1.41 ∙ 0.001 < 0

Logo, nosso novo intervalo será formado por a 5 e x 6 . Temos então que:

a 6 , b 6 = a 5 , x 6 = 0.2,0.567514

Critério de Parada:

b 6 - a 6 = 0.567514 - 0.2 = 0.367514 > 0.00001

f a 6 = 1.409438 > 0.00001

f b 6 = 0.001024 > 0.00001

Como não alcançamos o critério de parada continuamos as iterações.

a 6 , b 6 = 0.2,0.567514

ε 1 = ε 2 = 0.00001

Iteração 7 :

x 7 = a 6 f b 6 - b 6 f a 6 f b 6 - f a 6 = 0.80008 1.410461 = 0.567247

f x 7 = f 0.567247 ≅ 0.0003

f a 6 ∙ f x 7 = - 1.41 ∙ 0.0003 < 0

Logo, nosso novo intervalo será formado por a 6 e x 7 . Temos então que:

a 7 , b 7 = a 6 , x 7 = 0.2,0.567247

Critério de Parada:

b 7 - a 7 = 0.567247 - 0.2 = 0.367247 > 0.00001

f a 7 = 1.409438 > 0.00001

f b 7 = 0.000287 > 0.00001

Como não alcançamos o critério de parada continuamos as iterações.

a 7 , b 7 = 0.2,0.567247

ε 1 = ε 2 = 0.00001

Iteração 8 :

x 8 = a 7 f b 7 - b 7 f a 7 f b 7 - f a 7 = 0.799557 1.409725 = 0.567172

f x 8 = f 0.567172 ≅ 0.00008

f a 7 ∙ f x 8 = - 1.41 ∙ 0.00008 < 0

Logo, nosso novo intervalo será formado por a 7 e x 8 . Temos então que:

a 8 , b 8 = a 7 , x 8 = 0.2,0.567172

Critério de Parada:

b 8 - a 8 = 0.567172 - 0.2 = 0.367172 > 0.00001

f a 8 = 1.409438 > 0.00001

f b 8 = 0.00008 > 0.00001

Como não alcançamos o critério de parada continuamos as iterações.

a 8 , b 8 = 0.2,0.567247

ε 1 = ε 2 = 0.00001

Iteração 9 :

x 9 = a 8 f b 8 - b 8 f a 8 f b 8 - f a 8 = 0.79941 1.409518 = 0.567151

f x 9 = f 0.567151 ≅ 0.000023

f a 8 ∙ f x 9 = - 1.41 ∙ 0.000023 < 0

Logo, nosso novo intervalo será formado por a 8 e x 9 . Temos então que:

a 9 , b 9 = a 8 , x 9 = 0.2,0.567151

Critério de Parada:

b 9 - a 9 = 0.567151 - 0.2 = 0.367151 > 0.00001

f a 9 = 1.409438 > 0.00001

f b 9 = 0.000023 > 0.00001

Como não alcançamos o critério de parada continuamos as iterações.

a 8 , b 8 = 0.2,0.567247

ε 1 = ε 2 = 0.00001

Iteração 10 :

x 10 = a 9 f b 9 - b 9 f a 9 f b 9 - f a 9 = 0.799369 1.40946 = 0.567146

f x 10 = f 0.567146 ≅ 0.000006

f a 9 ∙ f x 10 = - 1.41 ∙ 0.000006 < 0

Logo, nosso novo intervalo será formado por a 9 e x 10 . Temos então que:

a 10 , b 10 = a 9 , x 10 = 0.2,0.567145

Critério de Parada:

b 10 - a 10 = 0.567146 - 0.2 = 0.367146 > 0.00001

f a 10 = 1.409438 > 0.00001

f b 10 = 0.000006 = 6 ∙ 10 - 6 < 0.00001

Ufa! Finalmente chegamos na precisão que queríamos! Esse é um exemplo clássico de uma situação em que esse método pode dar muuuuito errado. Repara que nós estávamos bem próximos da nossa aproximação desde a iteração 5 , mas quanto mais perto nós ficávamos mais lentamente a gente ia se aproximando! Se estivéssemos usando apenas a distância do intervalo como critério de parada por exemplo, íamos passar a vida toda aqui e não íamos chegar no resultado haha.

A raiz é então, com precisão de 10 - 5 , x - = 0.567146 .

Resposta

x - = 0.567146 .