Domínio de Funções de 3 Variáveis
Produzido por Bruno NeresTeoria
Restrições da função
Agora vamos ver como achar o domínio de funções de 3 variáveis, e vai ser basicamente a mesma coisa que fazíamos pra funções de 2 variáveis. A diferença é que agora o domínio não é mais uma região do plano, mas sim do espaço, ou seja: uma superfície.
Por isso é importante saber esboçar superfícies, porque algumas questões podem pedir o esboço dos domínios. Pra determinar o domínio temos que analisar as eventuais restrições da função, que são:
- raiz par: termo dentro dela não pode ser negativo
- quociente: denominador não pode valer zero
- logaritmo: termo dentro dele tem que ser estritamente positivo
Vamos achar e esboçar o domínio da função:
A única restrição da função é o logaritmo: o termo dentro dele tem que ser estritamente positivo. Ou seja:
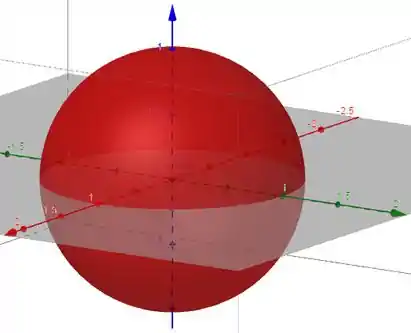
Portanto, o domínio da é o interior da esfera de raio 1 centrada na origem. Detalhe que a casca esférica em si não faz parte do domínio, porque na inequação temos “” e não “”.
O esboço fica:
Agora partiu treinar nos exercícios :)