Superfícies de Nível
Teoria
O que são e como calculá-las
Quando tínhamos uma função com 2 variáveis, as curvas de nível eram uma boa ferramenta pra visualizar o gráfico. Mas e se nós tivermos uma função com 3 variáveis? Nós vamos utilizar as superfícies de nível, que são o equivalente das curvas de nível pra funções de 3 variáveis.
Elas dão uma ideia do comportamento da função, e pra calculá-las também basta igualar a função a uma constante. Assim, a superfície de nível da função é dada por:
Agora vamos ver alguns exemplos!
Se quisermos descrever as superfícies de nível da função
Igualar a uma constante :
Que nada mais é que a equação de uma esfera de raio centrada na origem, quando . Porém se , a superfície de nível é o ponto e se não existem superfícies de nível.
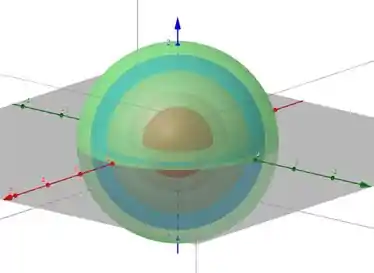
Em alguns casos o problema vai te fornecer um determinado ponto para você achar a curva de nível. Vamos de outro exemplo então!
Calculando a superfície de nível em um ponto
Agora a gente quer a superfície de nível da equação abaixo, em um determinado ponto
Vamos começar calculando o valor da função no ponto dado:
Beleza, então estamos tratando da superfície de nível 2 da função.
Agora igualamos a expressão da função ao valor achado, 2:
Isso já é a equação da superfície de nível, mas podemos ajeitar um pouco, deixando ela explícita, o que dá:
que é a equação de um paraboloide circular com vértice em . Olha a cara dele aí,
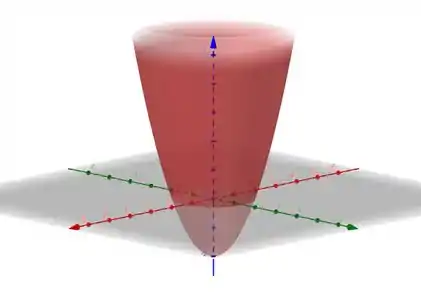
Beleza, agora vamos dar uma treinada nos exercícios, onde vão aparecer outras superfícies de nível mais complicadinhas!
Calculando a superfície de nível em um ponto
Exercícios Resolvidos
Exercício Resolvido #1
Howard Anton, Irl Bivens, Stephen Davis, Cálculo – Volume II, 8ª ed. Porto Alegre: ARTMED EDITORA S.A, 2005, p. 935 - 55
Seja
Determine uma equação da superfície de nível que passa pelo ponto
a)
b)
c)
Passo 1
a)
Vamos começar calculando o valor da função no ponto dado:
Beleza, então estamos tratando da superfície de nível 5 da função.
Passo 2
Agora igualamos a expressão da função ao valor achado, 5:
Isso já é a equação da superfície de nível, mas podemos ajeitar um pouco, deixando ela explícita, o que dá:
que é a equação de um paraboloide circular com vértice em .
Passo 3
b)
Vamos fazer exatamente a mesma coisa!
Calcular o valor da função no ponto:
Passo 4
Igualar função ao valor achado:
que também é um paraboloide circular.
Passo 5
c)
E agora, pra finalizar, vamos fazer o mesmo procedimento com a origem:
Ela se situa sobre a superfície de nível 0 da .
Passo 6
Igualamos a função a zero:
Resposta
a)
b)
c)
Exercício Resolvido #2
Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, p.78 – 12b
Descreva as superfícies de nível da função abaixo.
Passo 1
Para encontrar as superfícies de nível basta igualar a função a uma constante:
Tirando a exponencial nos dois lados:
Passo 2
Note que, para qualquer valor de , o lado direito da equação é sempre positivo. Portanto, se substituirmos , teremos que
E esta superfície é uma esfera de raio
Resposta
As superfícies de nível de são esferas de raio .
Exercício Resolvido #3
UFF, Lista 1, exercício 39
De acordo com a lei de gravitação universal de Newton, se uma partícula de massa está na origem de um sistema de coordenadas , então o módulo da força exercida sobre uma partícula de massa situada no ponto é dada por
Onde é a constante de gravitação universal. depende de quantas variáveis? Se e , descreva as superfícies de nível da função resultante.
Passo 1
Temos variáveis, a posição da partícula tem variáveis, , e e a quarta variável é a massa da partícula.
Passo 2
A superfície de nível tem a massa da partícula fixa, então passamos a ter uma superfície com dimensões. Se deixarmos a força , constante temos essas superfícies de nível.
Isso é uma esfera de raio
Resposta
Temos variáveis, a posição da partícula tem variáveis, , e e a quarta variável é a massa da partícula.
Isso é uma esfera de raio
Exercício Resolvido #4
Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, p.75 – exemplo 3.8
Descreva e esboce as superfícies de nível de .
Passo 1
Para encontrar as superfícies de nível basta igualar a função a uma constante:
Note que, para identificar essa superfície, temos que analisar o sinal da constante para cada caso: , e .
Passo 2
Se :
Podemos dividir os dois lados por :
Como , podemos dizer que , onde .
Esta superfície é um hiperboloide de uma folha, com eixo em .
Passo 3
Se :
Substituindo na equação:
Temos que
Esta superfície é um cone circular, com eixo em .
Passo 4
Se :
Podemos dividir os dois lados por :
Como , podemos dizer que , onde .
Esta superfície é um hiperboloide de duas folhas, com eixo em .
Resposta
Se : hiperboloide de uma folha
Se : cone circular
Se : hiperboloide de duas folhas
Exercício Resolvido #5
Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2000, p.77 -7ii(modificado)
Na figura estão representadas superfícies de nível da função . Escreva uma expressão adequada para .
Passo 1
De cara essa questão pode parecer meio bizarra, mas vamos destrinchar ela com calma.
Primeiro: essas superfícies são superfícies de nível da função, portanto elas são dadas pela equação geral
com variando de a , como podemos ver na figura.
Passo 2
Outra coisa: podemos ver que essas superfícies são planos paralelos ao plano , portanto planos de equação
Vou chamar essa nova constante de (nome bem original, eu sei). Se você prestar bem atenção na figura, vai ver que os valores de estão indicados no eixo. E esses números são justamente os valores de , variando de a .
Portanto, as 5 superfícies de nível mostradas têm equação dada por:
Passo 3
Beleza, agora o lance é comparar os com os . Por exemplo, no primeiro plano lá atrás, de equação , temos . Ou seja:
Ou seja, já podemos escrever uma expressão não muito profissional pra :
Certo? Já que quando , vale 3.
Passo 4
Vamos ver um dos outros planos pra ter mais informações sobre . Por exemplo a superfície de nível . Ela corresponde ao nível .
Opa, se vale zero então
Hmm, e justamente o vale . Já dá pra ter um palpite:
O que você acha? Isso dá certo pro que vimos antes.
O jeito é testar pras outras superfícies de nível!
Passo 5
Vamos pegar a superfície
Temos
Pelo nosso palpite, isso daria
Os valores estão batendo! E se a gente parar pra olhar as outras superfícies de nível, podemos ver que conforme o vai crescendo, o vai diminuindo linearmente, e vice-versa.
Então é isso mesmo, na base do “chute direcionado” achamos uma expressão adequada pra função: