Vetor Normal
Produzido por Bruno NeresTeoria
O que é?
Lembra que o vetor tangente é aquele que toca a curva em um determinado. A direção desse vetor indica o movimento desse vetor. Mas neste tópico a gente quer achar o vetor que é perpendicular ao vetor tangente, em outras palavras a gente quer achar o vetor normal.
E como a gente faz isso?
Primeiro, vamos visualizar esse vetor em uma curva qualquer,
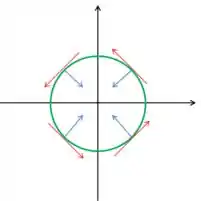
O vetor tangente está em vermelho e o vetor normal está em azul, perpendicular ao movimento. É valido ressaltar aqui que existem diversos vetores normais a trajetória de uma partícula, mas estudaremos aqui apenas aquele que aponta para o centro de curva.
Agora que a gente já visualizou, vamos calcular!
Como calcular?
Tá, agora como você faz pra encontrar esse vetor normal? A gente vai precisar de três passos:
- Achar o vetor tangente unitário;
- Achar a derivada do vetor tangente unitário;
- Com essas informações, calcularemos o vetor normal, por
Agora vamos para um exemplo para ver se entendemos o passo a passo!
Vamos encontrar o vetor normal a curva parametrizada por
Passo 1: A primeira coisa que temos que fazer é encontrar o vetor tangente, e a gente faz isso derivando :
Para saber o vetor tangente unitário, nós temos que dividir pelo módulo. Então vamos calcular o módulo
Pronto, agora é só dividir,
Passo 2: Agora vamos derivar esse vetor tangente unitário e achar o seu módulo:
Passo 3: Agora é só alegria! Vamos substituir na fórmula e achar nosso vetor normal
Só mais um coisinha, se você tiver se perguntando por que estamos aprendendo isso: mais à frente vamos calcular integrais de superfície em um campo vetorial, aí vamos precisar encontrar uma expressão para os vetores normais unitários em uma dada superfície.
Agora é hora de praticar fazendo alguns exercícios!