Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Singularidade

Ver Todos os Exercícios

Teoria

Fala, querido! Aqui a gente vai ver como usar o Teorema de Gauss mesmo temos uma singularidade. Como assim? Se liga no exemplo:

Calcule

∬ S   F → . n →   d s

Onde

F → x , y , z = - y x 2 + y 2 + z 2 , x x 2 + y 2 + z 2 , 1

E S é o cubo de lado 3, centrado na origem, com vetor normal externo a S .

Percebe que calcular essa integral pela definição vai ser chatinho porque o cubo é formado por 4 planos, ou seja, são 4 integrais para fazer. E além disso, esse campo é beem complicado de usar na integral com planos. Vamos usar o Teorema de Gauss, então? Vamo!

Mas temos um problema. Para aplicar Gauss a gente precisa que o campo esteja bem definido no interior da superfície S . Mas no ponto 0,0 , 0 (que fica dentro do cubo) os denominadores das componentes do nosso campo zeram. Isso quer dizer que F → não está definido na origem.

O que a gente faz então? Desiste de calcular essa integral de superfície aí?

Isso mesmo! Não vamos desistir. Esse ponto onde nosso campo não está definido e que está no interior de S nós chamamos de singularidade. A ideia aqui é a gente usar o Teorema de Gauss mesmo tendo essa singularidade dentro da nossa região fechada. Como? Vem ver!

Isolando a Singularidade

Vamos lembrar da fórmulinha do Teorema de Gauss

∬ ∂ W   F → . n →   d s = ∭ W   d i v F →   d V

Aí W é uma região fechada, que tem δ W como fronteira. No nosso caso, a fronteira seria S   (o cubo), e W seria a região dentro dele. Mas nós vimos que tem um problema com essa região W , ela tem uma singularidade, então não podemos usa-la.

A gente precisa de uma nova região W . A ideia aqui é introduzir uma nova superfície nessa situação, que envolva essa singularidade. Sendo que calcular a integral de superfície vetorial dessa nova superfície deve ser algo tranquilo de fazer.

Podemos introduzir, por exemplo, uma esfera de raio 1 e centro na origem. Por que? Cara a equação da esfera é

x 2 + y 2 + z 2 = 1

Repara que esse termo x 2 + y 2 + z 2 aparece no nosso campo F → . Isso é uma dica que de que a integral de superfície sobre essa esfera vai ser tranquila de calcular. Já já vamos ver o porquê.

Olha como fica nossa situação agora:

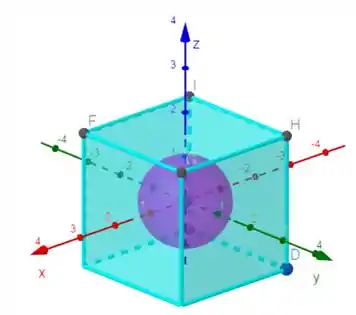
Então nossa nova região W agora pode ser a região dentro do cubo, mas fora da esfera. Aí percebe que 0,0 , 0 está dentro da esfera, então nossa nova região W não tem mais singularidade.

Se ela não tem mais singularidade, podemos aplicar Gauss sem problema! Aí já temos W . Mas quem vai ser δ W ? Cara, essa é a superfície que limita nossa região fechada.

Mas percebe que agora, nossa região está limitada pelo cubo S e pela esfera? Então para gente, δ W vai ser um conjunto de duas superfícies:

δ W = S + E s f e r a

Como a gente monta o nosso teorema agora? Tínhamos

∬ ∂ W   F → . n →   d s = ∭ W   d i v F →   d V

Vimos que δ W é a soma do cubo S com a esfera. Então ali no lado esquerdo teremos a soma de duas integrais de superfície, uma sobre o cubo e outra sobre a esfera

∬ S   F → . n →   d s + ∬ E s f e r a   F → . n →   d s = ∭ W   d i v F →   d V

Lembra que em integrais de superfície precisamos dar atenção a orientação das superfícies. E para usar o teorema de Gauss, os vetores normais dessas superfícies precisam apontar para fora da região W .

No enunciado, falamos que o vetor normal ao cubo é externo a ele, então beleza, está apontando para fora de W . Agora pensa na esfera. Se a região W está fora da esfera, os vetores normais a ela precisam apontar para o lado oposto, ou seja, para dentro da esfera.

Pronto, nosso teorema está montando! Como a gente quer calcular a nossa primeira integral, vamos isola-la

∬ S   F → . n →   d s = ∭ W   d i v F →   d V - ∬ E s f e r a   F → . n →   d s

Então o que precisamos fazer é calcular a integral tripla e a integral de superfície da esfera e diminuir uma da outra!

Com ficam os cálculos?

Vamos começar montando a integral tripla.

∭ W   d i v F →   d V

Aí precisamos resolver esse divergente! Que é calculado por

d i v F → = ∂ F 1 → ∂ x + ∂ F 2 → ∂ y + ∂ F 3 → ∂ z

Lembrando que: F → = F x , y , z = - y x 2 + y 2 + z 2 , x x 2 + y 2 + z 2 , 1

Então:

∂ F 1 → ∂ x =   - 2 x y x 2 + y 2 + z 2 2

∂ F 2 → ∂ y =   2 x y x 2 + y 2 + z 2 2

∂ F 3 → ∂ z = 0

d i v F → = ∂ F 1 → ∂ x + ∂ F 2 → ∂ y + ∂ F 3 → ∂ z = 0

Isso nos dá que

∭ W   d i v F →   d V = ∭ W   0   d V = 0

Agora que calculamos a integral tripla, vamos calcular a integral de superfície na esfera, resolvemos assim:

  1. Parametrizar a superfície:Como a superfície é uma esfera de raio 1 vamos usar as primas das coordenadas esféricas. x = s e n ϕ   c o s θ y =   s e n ϕ   s e n θ z = c o s ϕ
  2. Encontrar os limites de integração 0 ≤ θ ≤ 2 π 0 ≤ ϕ ≤ π
  3. Calcular F → φ ϕ , θ . É aqui que a gente percebe que escolher a esfera facilita a nossa vida. Olha como a expressão desse termo vai ficar mais tranquila

    4. F → = - y x 2 + y 2 + z 2 , x x 2 + y 2 + z 2 , 1

    Como a equação da esfera diz que x 2 + y 2 + z 2 é igual a 1 , só precisamos substituir 1 nesses denominadores com esse termo. E então substituir a parametrização normalmente:

    F → φ ϕ , θ = ( s e n θ s e n ϕ , - c o s θ s e n ϕ   , 1 )

  4. Encontrar n → d s , lembrando que a esfera tem o vetor normal apontando para dentro n → d s = N → d θ d ϕ N → = ∂ φ ∂ θ   X   ∂ φ ∂ ϕ Vamos usar matriz para calcular esse produto: i j k - s e n θ s e n ϕ c o s θ s e n ϕ 0 c o s θ c o s ϕ s e n θ c o s ϕ - s e n ϕ N → = - c o s θ s e n 2 ϕ , - s e n θ s e n 2 ϕ , - s e n θ c o s ϕ

    5. Como o nosso vetor normal deve apontar para a dentro da esfera, ou seja, apontar para a origem, todas as componentes devem ter sinal negativo, então já achamos nosso vetor certinho: N → = ( - c o s θ s e n 2 ϕ , - s e n θ s e n 2 ϕ , - s e n θ c o s ϕ )

  5. Agora que já temos F → e N → , vamos calcular a ∬ E s f e r a   F → . n →   d s

∫ 0 2 π ∫ 0 π ( ( s e n θ s e n ϕ , - c o s θ s e n ϕ   , 1 ) (   - c o s θ s e n 2 ϕ , - s e n θ s e n 2 ϕ , - s e n θ c o s ϕ ) d ϕ d θ ∫ 0 2 π ∫ 0 π - s e n ϕ c o s ϕ d ϕ d θ = 0

Agora que ja calculamos a integral tripla e a integral de superfície da esfera, vamos voltar ao teorema de Gauss e substituir os valores encontrados

∬ S   F → . n →   d s = ∭ W   d i v F →   d V - ∬ E s f e r a   F → . n →   d s

∬ S   F → . n →   d s = 0 - 0

Então, nesse caso, temos que:

∬ S   F → . n →   d s = 0

Deu pra pegar o jeitinho?

Então sempre que aparecer uma fração no seu campo, fica de olho se o denominador dela zera no interior de S . Se zerar, cê tem uma singularidade. Aí precisa isolar essa bonita com uma superfície nova para poder usar o Teorema de Gauss, tá bem?

Agora é partir pros exercícios e praticar!!

Isolando a Singularidade

Com ficam os cálculos?

Exercícios Resolvidos

Exercício Resolvido #1

UFRJ - Cálculo 3 - P2 2009.1 – 4

Considere o campo

F = x x 2 + y 2 + z 2 3 2 + 3 x , y x 2 + y 2 + z 2 3 2 , z x 2 + y 2 + z 2 3 2

Calcule o fluxo de F através das faces do cubo

W = x , y , z ∈ R 3 | - 2 ≤ x ≤ 2 ,   - 2 ≤ y ≤ 2 ,   - 2 ≤ z ≤ 2

Com vetores normais apontando para dentro.

Passo 1

O campo F é de classe C 1 em R 3 - ( 0,0 , 0 ) . Como a origem do sistema está no interior do cubo W , vamos isolá-la, considerando a esfera S 1 de raio 1 centrada na origem para, então, usar o teorema de Gauss na região R , que é interior ao cubo e exterior à esfera S 1 .

Chamando de S a fronteira do cubo, temos do teorema de Gauss:

∬ S ∪ S 1 F ∙ d S → = ∭ R d i v F d x   d y   d z

Onde estamos considerando os vetores normais de d S e de S ∪ S 1 apontando para fora da região R . O divergente de F é dado por

d i v F = ∂ F x ∂ x + ∂ F y ∂ y + ∂ F z ∂ z

Usando o F dado no enunciado:

∂ F x ∂ x = 1 x 2 + y 2 + z 2 3 2 - 3 x 2 x 2 + y 2 + z 2 5 2 + 3

∂ F y ∂ y = 1 x 2 + y 2 + z 2 3 2 - 3 y 2 x 2 + y 2 + z 2 5 2

∂ F z ∂ z = 1 x 2 + y 2 + z 2 3 2 - 3 z 2 x 2 + y 2 + z 2 5 2

d i v F = 3

Então, temos:

∬ S F ∙ d S → + ∬ S 1 F ∙ d S → = ∭ R d i v F d x   d y   d z = 3 ∭ R d x   d y   d z = 3   Volume R

Lembrando que a região R é o interior do cubo e o exterior da esfera,

∬ S F ∙ d S → + ∬ S 1 F ∙ d S → = ∭ R d i v F d x   d y   d z = 3 4 3 - 4 3 π = 192 - 4 π

Passo 2

Agora vamos calcular

∬ S 1 F ∙ d S → = ∬ S 1 F ∙ n →   d S

Observe que aqui estamos considerando o vetor normal unitário apontando para o interior da esfera S 1 . Observe também que, em cada ponto x , y , z ∈ S 1 , o vetor normal tem coordenadas   n → = ( - x , - y , - z ) . Logo,

F ∙ n → = - 3 x 2 - 1 x 2 + y 2 + z 2

Mas esse denominador x 2 + y 2 + z 2 é o próprio raio da esfera e, portanto, igual a 1. Então,

F ∙ n → = - 3 x 2 - 1

Assim:

∬ S 1 F ∙ n →   d S = - ∬ S 1 3 x 2 + 1 d S = - ∬ S 1 3 x 2 d S - 4 π

Em coordenadas esférias, temos:

x = cos ⁡ θ sen ⁡ ϕ

d S = sen ⁡ ( ϕ )   d θ   d ϕ

θ ∈ 0,2 π

ϕ ∈ 0 , π

Segue que:

∬ S 1 3 x 2 d S = ∫ 0 2 π ∫ 0 π 3 cos 2 ⁡ ( θ ) sen 3 ⁡ ( ϕ ) d θ   d ϕ = 4 π

Consequentemente:

∬ S 1 F ∙ n →   d S = - ∬ S 1 3 x 2 d S - 4 π

∬ S 1 F ∙ n →   d S = - 8 π

Somando tudo, levando em conta a mudança do vetor normal:

∬ S F ∙ d S → = 192 - 4 π + 8 π

∬ S F ∙ d S → = 192 + 4 π

Pois o fluxo dessa forma foi obtido com os vetores normais apontando para fora. Como queremos calcular o fluxo com os vetores apontando para dentro, a resposta é

- 192 + 4 π

Resposta

- 192 + 4 π

Exercício Resolvido #2

Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, pp. 308-12.

Calcule o fluxo do campo

F x ,   y ,   z = ( 2 x ,   - z x 2 + y 2 + z 2 - 1 2 ,   y x 2 + y 2 + z 2 - 1 2 )

Através da superfície S   definida pelas equações

x 2 4 + y 2 9 + z 2 25 = 1     ,                           z ≥ 0 x 2 4 + y 2 9 = 1     ,                     - 3 ≤ z ≤ 0 z =   - 3           ,                                 x 2 4 + y 2 9 ≤ 1

Passo 1

Primeiro vamos fazer um rascunho da imagem para entender melhor o problema!

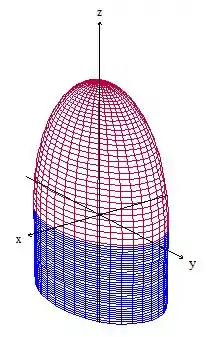
Passo 2

Está vendo a raiz no campo, bom devemos ficar atentos! Raiz e frações são sinais de singularidades, e aqui temos os dois!

O denominador x 2 + y 2 + z 2 , deve ser diferente de zero! Então o ponto ( 0 ,   0 ,   0 ) é uma singularidade.

Como dentro da raiz temos uma soma de quadrados, que é sempre maior que zero, a origem é a única singularidade!

Para retirar esta singularidade vamos definir uma esfera centrada na origem de raio R bem pequeno!

Assim, o Teorema de Gauss pode ser aplicado como,

∬ S 1   F → . n →   d S + ∬ S   F → . n →   d S = ∭ W   ∇ ⋅ F →   d V

Passo 3

Vamos começar calculando o divergente do campo,

∇ ⋅ F =   ∂ F 1 ∂ x +   ∂ F 2 ∂ y + ∂ F 3 ∂ z

∇ ⋅ F = 2 + y z x 2 + y 2 + z 2 - 3 2 + - y z x 2 + y 2 + z 2 - 3 2 = 2

Assim,

∭ W   ∇ ⋅ F →   d V = 2 ⋅ V W

Passo 4

Agora precisamos calcular o volume do sólido:

Volume do elipsoide, lembra que o volume de um elipsoide é dado por isso aqui?

V o l u m e e l i p s o i d e = 4 3 π   a b c

Onde a , b , c são as raízes dos denominadores de x 2 , y 2 e z 2 (os semeixos do elipsoide):

a = 2

b = 3

c = 5

Portanto, como queremos metade do elipsoide:

V e = 1 2 4 3 π   a b c = 20 π  

Volume do cilindro elíptico, a área de uma elipse é dada por:

a e = π a b

Onde a , b são as raízes dos denominadores de x 2 e y 2 (os semeixos da elipse), assim, o volume do cilindro é V c = π a b H , com a = 2 , b = 3 e H = 3 :

V c = π a b H = π ⋅ 2 ⋅ 3 ⋅ 3 = 18 π

Volume da esfera de raio R :

V e s f = 4 3 π R 3

Por fim,

2 ⋅ V w = 2 ⋅ 20 π + 18 π - 4 3 π R 3 = 76 π - 8 3 π R 3

Passo 5

Vamos calcular, ∬ S 1   F → . n →   d S , que representa o fluxo do campo que passa pela esfera de raio R . Para isso vamos parametrizar a esfera por:

φ θ , ϕ = ( R s e n ϕ c o s θ ,   R s e n ϕ s e n θ ,   R c o s ϕ )

0 ≤ ϕ ≤ π

0 ≤ θ ≤ 2 π

Vamos ver quanto dá esse vetor normal da esfera:

∂ φ ∂ ϕ = Rcos ⁡ θ cos ⁡ ϕ , R s e n θ cos ⁡ ϕ , - R s e n ϕ

∂ φ ∂ θ = - R s e n θ s e n ϕ , Rcos ⁡ θ s e n ϕ , 0

Calculando o produto vetorial:

n → =   ∂ φ ∂ ϕ × ∂ φ ∂ θ = i j k Rcos ⁡ θ cos ⁡ ϕ R s e n θ cos ⁡ ϕ - R s e n ϕ - R s e n θ s e n ϕ Rcos ⁡ θ s e n ϕ 0

n → =   ∂ φ ∂ ϕ × ∂ φ ∂ θ =   R 2 s e n 2 ϕ cos ⁡ θ , R 2 s e n 2 ϕ s e n θ , R 2 s e n ϕ cos ⁡ ϕ

n → =   ∂ φ ∂ ϕ × ∂ φ ∂ θ =   R 2 s e n ϕ s e n ( ϕ ) cos ⁡ θ , s e n ( ϕ ) s e n θ , cos ⁡ ϕ

∬ S 1   F → . n →   d S =   ∬ S 1   2 R s e n ϕ c o s θ ,   - c o s ϕ ,   s e n ϕ s e n θ ⋅ R 2 s e n ϕ s e n ϕ cos ⁡ θ , s e n ϕ s e n θ , cos ⁡ ϕ d S

∬ S 1   F → . n →   d S = ∫ 0 π ∫ 0 2 π ( 2 R 3 s e n 3 ϕ cos 2 ⁡ θ - R 2 s e n 2 ϕ c o s ϕ s e n θ + R 2 s e n 2 ϕ c o s ϕ s e n θ ) d θ d ϕ

∬ S 1   F → . n →   d S = ∫ 0 π ∫ 0 2 π ( 2 R 3 s e n 3 ϕ cos 2 ⁡ θ ) d θ d ϕ

∬ S 1   F → . n →   d S = ∫ 0 π ∫ 0 2 π 2 R 3 s e n 3 ϕ 1 + c o s 2 θ 2 d θ d ϕ

∬ S 1   F → . n →   d S = ∫ 0 π ∫ 0 2 π 2 R 3 s e n 3 ϕ θ 2 + s e n 2 θ 4 0 2 π d θ d ϕ

∬ S 1   F → . n →   d S = π ∫ 0 π 2 R 3 s e n 3 ϕ d ϕ

∬ S 1   F → . n →   d S = 2 π R 3 ∫ 0 π s e n 2 ϕ s e n ϕ d ϕ

Para resolver esta integral vamos usar:

u = c o s ϕ

d u = - s e n ϕ d ϕ

Ainda,

s e n 2 ϕ = 1 - cos 2 ⁡ ϕ = 1 - u 2

Assim, teremos:

∬ S 1   F → . n →   d S = 2 π R 3 ∫ 1 - 1 u 2 - 1 d u

∬ S 1   F → . n →   d S = 2 π R 3 u 3 3 - u 1 - 1 = 8 π R 3 3

Como a normal a esta espera está apontando para fora do sólido, o que significa estar apontando para a origem:

∬ S 1   F → . n →   d S = - 8 π R 3 3

Passo 6

Finalmente!! Teremos:

∬ S 1   F → . n →   d S + ∬ S   F → . n →   d S = ∭ W   ∇ ⋅ F →   d V

∬ S   F → . n →   d S = ∭ W   ∇ ⋅ F →   d V - ∬ S 1   F → . n →   d S  

∬ S   F → . n →   d S =   76 π - 8 3 π R 3 - - 8 π R 3 3 = 76 π  

∬ S   F → . n →   d S = 76 π

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #3

USP - Cálculo 3 - P3 2013 – 3

Calcule ∬ S   F → . N → d σ , onde

F → x , y , z = x i → + y j → + z k → x 2 + y 2 + z 2 3 / 2 + z 3 3 k →

E S é a superfície x 2 + y 2 4 + z 2 9 = 1 , orientada pela normal unitária exterior N → .

Passo 1

Essa função é realmente complicada, se tentarmos parametrizar a superfície S , que é um elipsoide, como temos x 2 + y 2 + z 2 na função F é interessante tentarmos usar o teorema de Gauss, isso porque é de boa escrever a superfície em coordenadas esféricas.

Vamos separar essa F → em duas funções F 1 e F 2 onde

F 1 = x i → + y j → + z k → x 2 + y 2 + z 2 3 2

E

F 2 = z 3 3 k

A integral vai ser a soma da integral de superfície de F 1 mais F 2 , vamos aplicar Gauss nas duas mas separamos porque uma vai dar um problema por não ter a origem definida, mas a outra é de boa facin de resolver.

Na F 1 não podemos aplicar o teorema de Gauss direto, mas podemos pegar uma segunda superfície S 2 sendo uma esfera de raio r que vai estar dentro do elipsoide.

S 2 : x 2 + y 2 + z 2 ≤ r

Ele vai estar dentro porque basta considerarmos r < 1 e os eixos do elipsoide são 1 , 2 e 3 todos maiores ou iguais a 1 , então essa esfera está dentro do elipsoide.

Vamos agora ao teorema de Gauss, primeiro em F 1 .

∬ S   F 1 → . N → d σ + ∬ S 2   F 1 → . N → d σ = ∭ W d i v F 1 → d x d y d z

Onde W é a região que tem como fronteira S ∪ S 2 .

Aplicando, agora, em F 2 , como não temos problemas com a função F 2 é só aplicar o teorema direto

∬ S   F 2 → . N → d σ = ∭ W d i v F 2 → d x d y d z

Onde W é a região que tem como fronteira S .

Passo 2

Vamos começar achando a integral de superfície em F 1

∬ S   F 1 → . N → d σ + ∬ S 2   F 1 → . N → d σ = ∭ W d i v F 1 → d x d y d z

Vamos começar achando a integral de superfície de S 2 , primeiro vamos ver como podemos escrever a parametrização de S 2 que é uma esfera de raio r , então temos

S 2 θ , ϕ = r ∙ cos ⁡ θ sen ⁡ ϕ , r ∙ sen ⁡ θ sen ⁡ ϕ , r ∙ cos ⁡ ϕ

S 2 θ , ϕ = r cos ⁡ θ sen ⁡ ϕ , r sen ⁡ θ sen ⁡ ϕ , r cos ⁡ ϕ

Com θ ∈ 0,2 π e ϕ ∈ 0 , π

Vamos achar o vetor normal, ele vai ser

N θ , ϕ = ∂ S 2 ∂ θ × ∂ S 2 ∂ ϕ

Vamos começar achando as derivadas da parametrização

∂ S 2 ∂ θ = - r sen ⁡ θ sen ⁡ ϕ , r cos ⁡ θ sen ⁡ ϕ , 0

∂ S 2 ∂ ϕ = r cos ⁡ θ cos ⁡ ϕ , r sen ⁡ θ cos ⁡ ϕ , - r sen ⁡ ϕ

O vetor normal vai ser

N θ , ϕ = i j k - r sen ⁡ θ sen ⁡ ϕ r cos ⁡ θ sen ⁡ ϕ 0 r cos ⁡ θ cos ⁡ ϕ r sen ⁡ θ cos ⁡ ϕ - r sen ⁡ ϕ

N θ , ϕ = - r 2 sen 2 ⁡ ϕ cos ⁡ θ i + 0 j + - r 2 sen 2 ⁡ θ sen ⁡ ϕ cos ⁡ ϕ k - r 2 cos 2 ⁡ θ sen ⁡ ϕ cos ⁡ ϕ k - r 2 sen 2 ⁡ ϕ sen ⁡ θ j - 0 i

N θ , ϕ = - r 2 sen 2 ⁡ ϕ cos ⁡ θ i + - r 2 sen 2 ⁡ θ sen ⁡ ϕ cos ⁡ ϕ - r 2 cos 2 ⁡ θ sen ⁡ ϕ cos ⁡ ϕ k - r 2 sen 2 ⁡ ϕ sen ⁡ θ j

N θ , ϕ = - r 2 sen 2 ⁡ ϕ cos ⁡ θ i + - r 2 sen ⁡ ϕ cos ⁡ ϕ sen 2 ⁡ θ + cos 2 ⁡ θ k - r 2 sen 2 ⁡ ϕ sen ⁡ θ j

N θ , ϕ = - r 2 sen 2 ⁡ ϕ cos ⁡ θ i + - r 2 sen ⁡ ϕ cos ⁡ ϕ k - r 2 sen 2 ⁡ ϕ sen ⁡ θ j

Repara que esse vetor esse vetor está todo negativo, isso vai fazer ele sempre apontar para dentro da esfera, então ele está com a orientação correta que queremos que é apontar para fora de W .

Passo 3

Vamos calcular a integral de superfície

∬ S 2   F → . N → d σ

Repara que a função vai ser

F → = x i → + y j → + z k → x 2 + y 2 + z 2 3 / 2 k →

F → = x x 2 + y 2 + z 2 3 / 2 , y x 2 + y 2 + z 2 3 / 2 , z x 2 + y 2 + z 2 3 / 2

Substituindo os valores da superfície S 2 , é importante entender que aquele denominador vai ser 1 isso porque

x 2 + y 2 + z 2

⇒ cos ⁡ θ sen ⁡ ϕ 2 + sen ⁡ θ sen ⁡ ϕ 2 + cos ⁡ ϕ 2

⇒ cos 2 ⁡ θ sen 2 ⁡ ϕ + sen 2 ⁡ θ sen 2 ⁡ ϕ + cos 2 ⁡ ϕ

⇒ cos 2 ⁡ θ + sen 2 ⁡ θ sen 2 ⁡ ϕ + cos 2 ⁡ ϕ

⇒ 1 sen 2 ⁡ ϕ + cos 2 ⁡ ϕ

⇒ 1

A integral vai ficar

∬ S 2   F → S 2 ∙ N → θ , ϕ d ϕ d θ

⇒ ∫ 0 2 π ∫ 0 π cos ⁡ θ sen ⁡ ϕ 1 3 2 , sen ⁡ θ sen ⁡ ϕ 1 3 2 , cos ⁡ ϕ 1 3 2 - sen 2 ⁡ ϕ cos ⁡ θ , - sen 2 ⁡ ϕ sen ⁡ θ , - sen ⁡ ϕ cos ⁡ ϕ d ϕ d θ

⇒ ∫ 0 2 π ∫ 0 π - sen 3 ⁡ ϕ cos 2 ⁡ θ - sen 2 ⁡ θ sen 3 ⁡ ϕ - sen ⁡ ϕ cos 2 ⁡ ϕ d ϕ d θ

⇒ ∫ 0 2 π ∫ 0 π - sen 3 ⁡ ϕ cos 2 ⁡ θ + sen 2 ⁡ θ - sen ⁡ ϕ cos 2 ⁡ ϕ d ϕ d θ

⇒ ∫ 0 2 π ∫ 0 π - sen 3 ⁡ ϕ - sen ⁡ ϕ cos 2 ⁡ ϕ d ϕ d θ

⇒ ∫ 0 2 π ∫ 0 π - sen ⁡ ϕ sen 2 ⁡ ϕ + cos 2 ⁡ ϕ d ϕ d θ

⇒ ∫ 0 2 π ∫ 0 π - sen ⁡ ϕ d ϕ d θ

⇒ ∫ 0 2 π cos ⁡ ϕ ϕ = 0 π d θ

⇒ ∫ 0 2 π cos ⁡ π - cos ⁡ 0 d θ

⇒ ∫ 0 2 π - 1 - 1 d θ

⇒ ∫ 0 2 π - 2 d θ

⇒ - 2 θ 0 2 π

⇒ - 4 π

Passo 4

Vamos para a integral tripla agora, primeiro vamos achar o divergente

d i v F 1 → = ∂ F 1 x ∂ x + ∂ F 1 y ∂ y + ∂ F 1 z ∂ z

d i v F 1 → = - 2 x 2 + y 2 + z 2 x 2 + y 2 + z 2 5 / 2 + x 2 - 2 y 2 + z 2 x 2 + y 2 + z 2 5 / 2 + x 2 + y 2 - 2 z 2 x 2 + y 2 + z 2 5 / 2

d i v F 1 → = - 2 x 2 + y 2 + z 2 + x 2 - 2 y 2 + z 2 + x 2 + y 2 - 2 z 2 x 2 + y 2 + z 2 5 / 2

d i v F 1 → = 0 x 2 + y 2 + z 2 5 / 2

d i v F 1 → = 0

Passo 5

Voltando para a integral no início do passo 2

∬ S   F 1 → . N → d σ + ∬ S 2   F 1 → . N → d σ = ∭ W d i v F 1 → d x d y d z

Então vamos ter

∬ S   F 1 → . N → d σ + - 4 π = 0

∬ S   F 1 → . N → d σ = 4 π

Passo 6

Vamos agora para F 2

∬ S   F 2 → . N → d σ = ∭ W d i v F 2 → d x d y d z

Aqui o divergente vai ficar

d i v F 2 → = ∂ F 2 x ∂ x + ∂ F 2 y ∂ y + ∂ F 2 z ∂ z

d i v F 2 → = 0 + 0 + 3 z 2 3

d i v F 2 → = z 2

Então a integral vai ficar

∭ W d i v F 2 → d x d y d z = ∭ W z 2 d x d y d z

Passo 7

Vamos resolver aquela integral tripla, para isso vamos usar coordenadas esféricas, mas dando uma adaptada ao elipsoide.

x = ρ cos ⁡ θ sen ⁡ ϕ

y = 2 ρ sen ⁡ θ sen ⁡ ϕ

z = 3 ρ cos ⁡ ϕ

Esse 2 e 3 são os eixos do elipsoide, assim vamos ter ρ entre 0 e 1 , mas temos que ficar atentos que o jacobiano vai ficar multiplicado por 2 e 3 .

J = 6 ρ 2 sen ⁡ ϕ

Como temos o elipsoide completo vamos ter θ ∈ 0,2 π e ϕ ∈ 0 , π

A integral vai ficar

∭ W z 2 d x d y d z = ∫ 0 2 π ∫ 0 π ∫ 0 1 3 ρ cos ⁡ ϕ 2 6 ρ 2 sen ⁡ ϕ d ρ d ϕ d θ

⇒ ∫ 0 2 π ∫ 0 π ∫ 0 1 9 ρ 2 cos 2 ⁡ ϕ 6 ρ 2 sen ⁡ ϕ d ρ d ϕ d θ

⇒ 54 ∫ 0 2 π ∫ 0 π ∫ 0 1 ρ 4 cos 2 ⁡ ϕ sen ⁡ ϕ d ρ d ϕ d θ

⇒ 54 ∫ 0 2 π ∫ 0 π ρ 5 5 ρ = 0 1 cos 2 ⁡ ϕ sen ⁡ ϕ d ϕ d θ

⇒ 54 ∫ 0 2 π ∫ 0 π 1 5 5 - 0 5 5 cos 2 ⁡ ϕ sen ⁡ ϕ d ϕ d θ

⇒ 54 ∫ 0 2 π ∫ 0 π 1 5 cos 2 ⁡ ϕ sen ⁡ ϕ d ϕ d θ

⇒ 54 5 ∫ 0 2 π ∫ 0 π cos 2 ⁡ ϕ sen ⁡ ϕ d ϕ d θ

Vamos resolver essa integral separado no próximo passo

Passo 8

∫ cos 2 ⁡ ϕ sen ⁡ ϕ d ϕ

Vamos fazer

cos ⁡ ϕ = u

Derivando

d u = - sen ⁡ ϕ d ϕ

sen ⁡ ϕ d ϕ = - d u

A integral vai ficar

∫ cos 2 ⁡ ϕ sen ⁡ ϕ d ϕ = ∫ - u 2 d u

⇒ - u 3 3 + C

Voltando para ϕ

- u 3 3 + C = - cos 3 ⁡ ϕ 3 + C

Como temos uma integral definida vamos ignorar esse C

Passo 9

54 5 ∫ 0 2 π - cos 3 ⁡ ϕ 3 ϕ = 0 π d θ

⇒ 54 5 ∫ 0 2 π - cos 3 ⁡ π 3 - - cos 3 ⁡ 0 3 d θ

⇒ 54 5 ∫ 0 2 π - - 1 3 3 - - 1 3 3 d θ

⇒ 54 5 ∫ 0 2 π 1 3 + 1 3 d θ

⇒ 54 5 ∫ 0 2 π 2 3 d θ

⇒ 54 5 2 3 θ θ = 0 2 π

⇒ 54 5 2 3 2 π - 0

⇒ 54 5 2 3 2 π

⇒ 72 π 5

Passo 10

Vamos ter

∬ S   F → . N → d σ = ∬ S   F 1 → . N → d σ + ∬ S   F 2 → . N → d σ

∬ S   F → . N → d σ = 4 π + 72 π 5

∬ S   F → . N → d σ = 92 π 5

Resposta

92 π 5

Exercício Resolvido #4

USP - Cálculo 3 - PSUB 2014 – 3

Seja

F → x , y , z = 4 ( x , y , z ) x 2 + y 2 + z 2 3 / 2 + x , y , x 2

Calcule ∬ S   F → ∙ n → d S , onde S é a parte do parabolóide z = 1 - x 2 - y 2 com x 2 + y 2 ≤ 1 , orientada com a normal unitária n → 0,0 , 1 = ( 0,0 , 1 ) .

Passo 1

Ele quer aquela integral de superfície ao longo daquela função F → , repara que ele colocou essa parada divida em duas funções, vamos pensar então na F → como

F → = F 1 → + F 2 →

Com

F 1 → = 4 ( x , y , z ) x 2 + y 2 + z 2 3 / 2

E

F 2 → = x , y , x 2

Vamos fazer cada uma das integrais para cada um desses dois campos separado e depois é só somar.

∬ S   F → ∙ n → d S = ∬ S   F 1 → ∙ n → d S + ∬ S   F 2 → ∙ n → d S

Passo 2

Vamos começar fazendo

∬ S   F 2 → ∙ n → 2 d S

Para isso, precisamos parametrizar S , certo? Como se trata de um paraboloide, e paraboloide ficam “bem” em coordenadas cilíndricas, são elas que vamos usar:

x = r cos ⁡ θ

y = r   s e n   θ

z = z

Levando para a equação do paraboloide, temos:

z = 1 - r 2

Ou seja, sua parametrização é:

φ r , θ = r cos ⁡ θ ,   r   s e n   θ , 1 - r 2

Onde

x 2 + y 2 ≤ 1

O que quer dizer que 0 ≤ r ≤ 1 .

Como se trata de uma volta completa em torno de z , 0 ≤ θ ≤ 2 π .

Passo 3

Agora vamos calcular a normal à superfície:

∂ φ ∂ r = cos ⁡ θ ,   s e n   θ , - 2 r

∂ φ ∂ θ = - r   s e n   θ ,   r cos ⁡ θ , 0

∂ φ ∂ r × ∂ φ ∂ θ = i j k cos ⁡ θ s e n   θ - 2 r - r   s e n   θ r cos ⁡ θ 0 = 2 r 2 cos ⁡ θ , 2 r 2 s e n   θ , r 2

Passo 4

Agora vamos montar a integral. Escrevendo o campo em função da parametrização:

F φ = r cos ⁡ θ ,   r   s e n   θ ,   r 2 cos 2 ⁡ θ

Levando tudo o que temos para a integral:

∬ S   F 2 → ∙ n → 2 d S = ∫ 0 2 π ∫ 0 1 r cos ⁡ θ ,   r   s e n   θ ,   r 2 cos 2 ⁡ θ . 2 r 2 cos ⁡ θ , 2 r 2 s e n   θ , r 2 d r d θ

= ∫ 0 2 π ∫ 0 1 2 r 3 cos 2 ⁡ θ + 2 r 3 s e n 2   θ + r 4 cos 2 ⁡ θ d r d θ =

= ∫ 0 2 π ∫ 0 1 2 r 3 + r 4 cos 2 ⁡ θ d r d θ =

= ∫ 0 2 π r 4 2 + r 5 5 cos 2 ⁡ θ 0 1 d θ =

= ∫ 0 2 π 1 2 + 1 5 cos 2 ⁡ θ d θ =

Lembrando que

cos 2 ⁡ θ = 1 + cos ⁡ 2 θ 2

= 1 2 ∫ 0 2 π 1 + 1 + cos ⁡ 2 θ d θ =

= 1 2 ∫ 0 2 π 2 + cos ⁡ 2 θ d θ =

= θ + 1 4 s e n   2 θ 0 2 π =

= 2 π

Passo 5

Agora a gente precisa calcular a outra parte da integral

∬ S   F 1 → ∙ n → d S

Mas esse campo tem uma expressão bizarra, não é?

F 1 → = 4 ( x , y , z ) x 2 + y 2 + z 2 3 / 2

Vamos calcular o divergente disso aí então e rezar pra ser algo bonito:

d i v F 1 → = ∂ ∂ x 4 x x 2 + y 2 + z 2 3 2 + ∂ ∂ y 4 y x 2 + y 2 + z 2 3 2 + ∂ ∂ z 4 z x 2 + y 2 + z 2 3 2

d i v F 1 → = 4 - 2 x 2 + y 2 + z 2 x 2 + y 2 + z 2 5 2 + 4 x 2 - 2 y 2 + z 2 x 2 + y 2 + z 2 5 2 + 4 x 2 + y 2 - 2 z 2 x 2 + y 2 + z 2 5 2

d i v F 1 → = 0

Olha que maravilha!!

Passo 6

Partiu usar Gauss então, né? MUITA CALMA NESSA HORA. A gente precisa de uma superfície fechada para aplicar o teorema.

Nossa superfície é essa aqui:

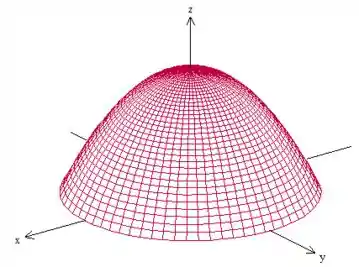
Nada mais natural que fechar isso aí com um círculo embaixo, né? Agora olha de novo para o campo:

F 1 → = 4 ( x , y , z ) x 2 + y 2 + z 2 3 / 2

Repara que ele não está definido em x = y = z , ou seja: NÃO PODEMOS fechar com esse círculo nem com qualquer superfície que contenha a origem.

Precisamos tirar a origem da região. Ok, como temos vários termos quadráticos no campo, vamos fazer isso com uma casa de esfera:

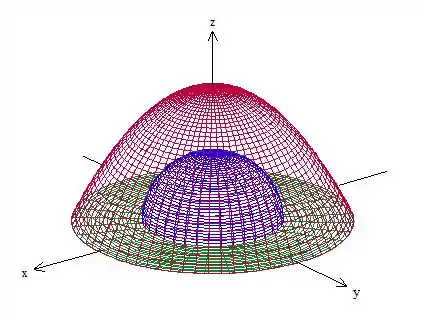
Pronto, isolamos a origem. Assim, a fronteira da região passa a de o paraboloide S , com a semiesfera E e o anel plano A .

Que bagunça, né? É a vida, vamos lá. Finalmente, podemos apicar Gauss:

∬ S F 1 → ∙ n → d S + ∬ E F 1 → ∙ n → d S + ∬ A F 1 → ∙ n → d S = ∭ W d i v F 1 → d W = 0

Foi? Então, a integral que queremos é isso aqui:

∬ S F 1 → ∙ n → d S = - ∬ E F 1 → ∙ n → d S - ∬ A F 1 → ∙ n → d S

Onde as normais apontam para fora de W .

Passo 7

Calma, gente, tá acabando. Precisamos, então, dessas duas integrais. Vamos começar pelo anel que pertence ao plano z = 0 .

Tá, como nós sabemos que o raio máximo do paraboloide é r = 1 (pelo enunciado), vamos assumir que essa nossa esfera tem raio 1 / 2 . Agora precisamos parametrizar o anel, certo?

Repara que a sua parametrização vai ser uma coisa assim:

A x , y = ( x , y , 0 )

Onde 1 / 2 ≤ x 2 + y 2 ≤ 1 .

E sua normal vai ser uma coisa assim:

n = ( ? , ? , 0 )

Beleza? Agora olha isso aqui:

∬ A F 1 → ∙ n → d S = ∬ D   F ( A y , y ) . n d S

Escrevendo o campo em função da parametrização, temos:

F 1 → = 4 ( x , y , 0 ) x 2 + y 2 + z 2 3 / 2

Agora chora de alegria comigo:

∬ A F 1 → ∙ n → d S = ∬ D   4 ( x , y , 0 ) x 2 + y 2 + z 2 3 / 2 ( ? , ? , 0 ) d S = 0

Por milagre divino esse produto escalar é zero :D É, só que a questão ainda não acabou.

Passo 8

Agora vamos calcular a integral na esfera E .

Lembrando que

E = x , y , z ∈ R 3 x 2 + y 2 + z 2 = 1 / 4 , z ≥ 0

Respira fundo e vamos continuar, essa questão é levemente gigante né mas fazer o que.

Para achar o vetor normal vamos fazer

f x , y , z = x 2 + y 2 + z 2 - 1 / 4

Então

n → = ∇ f

n → = 2 x , 2 y , 2 z

Fica atento a orientação do vetor, que deve estar orientado para fora de W , portanto, para baixo na esfera. Então, como, z ≥ 0 vetor normal na verdade vai ser trocando o sinal desse vetor que achamos

n → = - 2 x , - 2 y , - 2 z

Um detalhe importante é que quando achamos o vetor normal pelo gradiente temos que normalizar esse vetor, vamos fazer

n → = - 2 x , - 2 y , - 2 z - 2 x 2 + - 2 y 2 + - 2 z 2

n → = - 2 x , - 2 y , - 2 z 4 x 2 + 4 y 2 + 4 z 2

n → = - 2 x , - 2 y , - 2 z 4 x 2 + y 2 + z 2

Lembrando que para essa esfera temos

x 2 + y 2 + z 2 = 1 / 4

n → = - 2 x , - 2 y , - 2 z 1

n → = 2 - x , - y , - z

A nossa integral vai ficar

∬ e F 1 → ∙ n → d S = ∬ E 4 x , y , z x 2 + y 2 + z 2 3 2 ∙ 2 - x , - y , - z d S =

= 8 ∬ E - x 2 - y 2 - z 2 x 2 + y 2 + z 2 3 2 d S =

= 8 ∬ E - 1 x 2 + y 2 + z 2 x 2 + y 2 + z 2 3 2 d S

= 8 ∬ E - 1 x 2 + y 2 + z 2 1 2 d S

Lembra também que em E vamos ter

x 2 + y 2 + z 2 = 1 / 4

Então

∬ E - 2 d S = - 2 Á r e a E

Então queremos a área da metade de uma esfera de raio 1 / 2 , então

Á r e a E = 4 π . ( 1 / 2 ) 2 2 = π 2

Assim nossa integral de superfície vai ficar

∬ E F 1 → ∙ n → d S = - π 2

Passo 9

Vamos juntar a parada toda agora

∬ S   F → ∙ n → d S = ∬ S   F 1 → ∙ n → d S + ∬ S   F 2 → ∙ n → d S ⏟ 2 π

∬ S   F → ∙ n → d S = ∬ S   F 1 → ∙ n → d S + 2 π

E nós temos:

∬ S F 1 → ∙ n → d S = - ∬ E F 1 → ∙ n → d S ⏟ - π 2 - ∬ A F 1 → ∙ n → d S ⏟ 0 = π 2

Portanto, o que queremos é:

∬ S   F → ∙ n → d S = π 2 + 2 π = 5 π 2

ALELUIA!!!

Resposta

5 π 2