Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Superfície Aberta

Ver Todos os Exercícios

Teoria

Teorema de Gauss

Pelo Teorema de Gauss, a gente consegue transformar uma integral de superfície em uma integral tripla, como descrito aqui embaixo,

∬ ∂ W   F → . n →   d s = ∭ W   d i v F →   d V

Ou seja, ele nos ajuda a resolver algumas integrais mais complicadas com essa transformação. Porém, o Teorema de Gauss é usado para superfícies fechadas, nas quais é possível calcular o volume! Mas e se tivermos uma superfície aberta, o que fazer?

Vamos fechar a superfície! E é isso que vamos aprender neste tópico.

Superfícies Abertas

Vamos resolver um exemplo para entender como vamos fechar essa superfície e calcular essa integral.

F → = e y 2 ; ln ⁡ z 2 + 1 ; x 2 S : z = 9 - x 2 + y 2                    

Onde, 0 ≤ z ≤ 9 e n → . k → > 1

Então, se a gente tentar resolver essa integral de superfície diretamente vai ser complicado, por isso vamos aplicar o Teorema de Gauss. Mas lembra que a superfície tem que ser fechada? Vamos ver como é essa superfície S no gráfico,

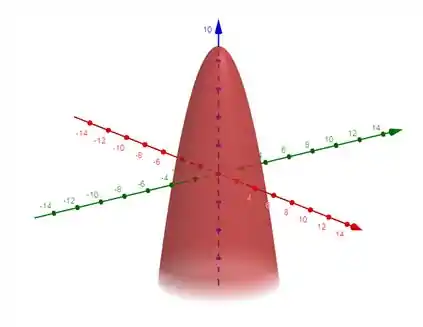
Repara que a superfície é aberta na parte de baixo, então é ali que vamos ter que fechar!

Galerinha, sempre que a superfície tiver um perfil de paraboloide, cone ou cilindro, desconfie, pois pode tratar-se de uma superfície aberta.

Seguindo, vamos agora fechar a superfície! Para isso nós vamos adicionar uma superfície S 1 embaixo do paraboloide, como indicado na figura,

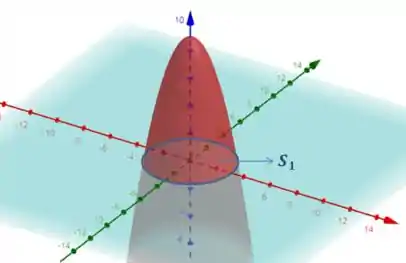
Como a gente adicionou mais uma superfície, o nosso teorema de Gauss agora terá essa cara aqui,

∬ S 1   F → . n →   d s + ∬ ∂ W   F → . n →   d s = ∭ W   d i v F →   d V

Note que apareceu uma integral de superfície para S 1 . Agora vamos resolver essa nova integral que foi formada!

∬ S 1   F → . n →   d s

Mas antes vamos olhar para ela no plano x y que tem essa cara aqui,

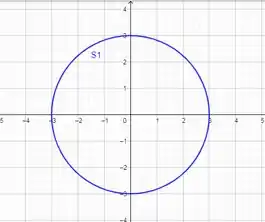
Repara que a nossa “tampa” é uma circunferência de raio 3 , em z = 0 . Então a parametrização dela ficará assim,

S 1 : φ = r c o s θ ; r s e n θ ; 0

Como o raio vai até 3 , nós temo que 0 ≤ r ≤ 3 .

Já o θ vai variar de 0 ≤ θ ≤ 2 π , pois os círculo é completo.

Seguindo para resolvendo a integral da “tampa”, vamos achar o vetor normal,

n → = i j k c o s θ s e n θ 0 - r s e n θ r c o s θ 0 = 0,0 , r

Só mais uma coisinha, como a “tampa” está embaixo da nossa superfície e nosso vetor normal aponta para fora da superfície, ele vai ter que apontar para baixo. Ele fica assim,

n → = 0,0 , - r

Achamos o nosso vetor normal, vamos para nosso campo que está definido em,

F → = e y 2 ; ln ⁡ z 2 + 1 ; x 2

Como já parametrizamos nossa circunferência, vamos fazer a substituição,

F → φ r , θ = e ( r s e n θ ) 2 ; 0 ; r ² c o s 2 θ

Agora vamos voltar para integral de S 1 , que ficará assim,

∬ S 1   e ( r s e n θ ) 2 ; 0 ; r ² c o s 2 θ . 0,0 , - r   d r d θ

Vamos colocar nossos limites de integração e resolver nossa integral,

∫ 0 2 π ∫ 0 3 - r ³ c o s 2 θ   d r d θ =   - 81 π 4

Pronto, calculada a integral de superfície da “tampa”, vamos voltar para nossa equação geral de novo,

∬ S 1   F → . n →   d s + ∬ ∂ W   F → . n →   d s = ∭ W   d i v F →   d V

- 81 π 4 + ∬ ∂ W   F → . n →   d s = ∭ W   d i v F →   d V

Então para resolver a nossa equação de superfície original, nós temos que

∬ ∂ W   F → . n →   d s = ∭ W   d i v F →   d V + 81 π 4

Então galera, o que a gente precisa agora é só achar o nosso divergente para resolver a integral tripla,

d i v F → = ∂ F 1 ∂ x +   ∂ F 2 ∂ y + ∂ F 3 ∂ z

Lembra, que o nosso campo é F → = e y 2 ; ln ⁡ z 2 + 1 ; x 2

Então calculando as derivadas parciais temos, que

d i v F → = 0 +   0 + 0

d i v F → = 0

Então nossa integral tripla será zero,

∭ W   d i v F →   d V = 0

Voltando para nossa o nosso problema, ficamos assim

∬ ∂ W   F → . n →   d s = 0 + 81 π 4

∬ ∂ W   F → . n →   d s = + 81 π 4

Pronto! Acabamos de resolver o nosso exemplo!

Importante!!

Ao usar o Teorma de Gauss a superfície do sólido é dita orientada positivamente caso o vetor normal em qualquer ponto esteja apontando para fora da superfície!

Devemos tomar cuidado ao fechar o sólido, a nova superfície, ou seja, a tampa deve manter a orientação da superfície, resultando num sólido orientado positivamente!

Observação: Uma relação importante é a do divergente do rotacional, ao fazer está operação temos um resultado interessante! Veja só!

Seja um campo vetorial F → = F 1 ,   F 2 ,   F 3 , assim

r o t F → = i j k ∂ ∂ x ∂ ∂ y ∂ ∂ z F ! F 2 F 3 = ∂ F 3 ∂ y - ∂ F 2 ∂ z ,   ∂ F 1 ∂ z - ∂ F 3 ∂ x ,   ∂ F 2 ∂ x - ∂ F 1 ∂ y

G → = r o t F → =   ∂ F 3 ∂ y - ∂ F 2 ∂ z ,   ∂ F 1 ∂ z - ∂ F 3 ∂ x ,   ∂ F 2 ∂ x - ∂ F 1 ∂ y

Agora vamos fazer o divergente de G → ,

d i v G → = ∂ G 1 ∂ x +   ∂ G 2 ∂ y + ∂ G 3 ∂ z

d i v G → =   ∂ 2 F 3 ∂ y ∂ x - ∂ 2 F 2 ∂ z ∂ x +   ∂ 2 F 1 ∂ z ∂ y - ∂ 2 F 3 ∂ x ∂ y + ∂ 2 F 2 ∂ x ∂ z - ∂ 2 F 1 ∂ y ∂ z

d i v G → = 0

Como G → = r o t F → ,

d i v r o t F → = 0

Pronto! Então todo divergente do rotacional é zero! Mas pra que diabos alguém usaria isso?

Bom, em algumas questões malignas você pode ter que usar Gauss e Stokes juntos! Pois é, nego perde a linha né? Mas é isso aí, bora praticar um pouco!

E agora vamos partiu exercícios?!

Exercícios Resolvidos

Exercício Resolvido #1

USP - Cálculo 3 - PSUB 2012 – 4

Calcule ∬ S   F → . N → d S onde F → x , y , z = e y 2 + x , y + 1 , z e S é a parte da superfície 4 x 2 + y 2 + 2 z 2 = 4 com y ≥ 0 sendo N → a normal tal que N → . j → ≥ 0 .

Passo 1

Vamos começar com um esboço da região para entender melhor o que está acontecendo. Temos o elipsoide:

x 2 + y 2 4 + z 2 2 = 1

Com y ≥ 0 . É isso aqui então:

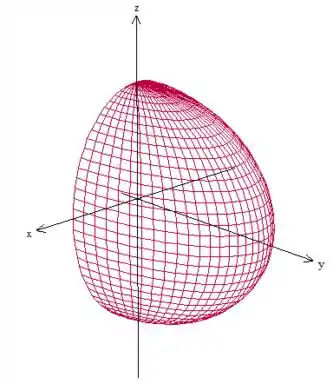
Passo 2

Como deve dar trabalho calcular isso ai pela definição (dá uma olhada no campo), vamos tentar usar Gauss aqui. Começarmos calculando esse divergente:

d i v F → = ∂ F 1 ∂ x +   ∂ F 2 ∂ y + ∂ F 3 ∂ z

d i v F → = 1 + 1 + 1 = 3

Olha que maravilha isso aqui.

Passo 3

Para usar Gauss, precisamos fechar essa região. Vamos fechar com esse disco (elipse) que a borda de S forma, pode ser? Então, temos isso aqui:

∬ S   F → . n →   d s + ∬ e   F → . n →   d s = ∭ w   d i v F →   d V

Sendo W a região na figura acima, orientada positivamente, e e é a elipse que fecha S . Temos então:

∬ S   F → . n →   d s = 3 ∭ w   d V - ∬ e   F → . n →   d s

∬ S   F → . n →   d s = 3 V o l u m e ( W ) - ∬ e   F → . n →   d s

Onde V o l u m e ( W ) é metade do volume do elipsoide. Lembra que o volume de um elipsoide é dado por isso aqui?

V o l u m e e l i p s o i d e = 4 3 π   a b c

Onde a , b , c são as raízes dos denominadores de x 2 , y 2 e z 2 (os semeixos do elipsoide):

a = 1

b = 2

c = 2

Portanto:

V o l u m e e l i p s o i d e = 8 π 2   3  

Isso nos dá:

∬ S   F → . n →   d s = 3 × 1 2 × 8 π 2   3 - ∬ e   F → . n →   d s

∬ S   F → . n →   d s = 4 π 2 - ∬ e   F → . n →   d s

Passo 4

Agora precisamos da integral na elipse. Para descobrir sua equação vamos fazer y = 0 na equação do elipsoide:

x 2 + 0 + z 2 2 = 1

x 2 + z 2 2 = 1

Vamos parametrizar isso aí em coordenadas elípticas então:

φ r , θ = r cos ⁡ θ ,   0 , 2 r s e n   θ  

Onde 0 ≤ θ ≤ 2 π e 0 ≤ r ≤ 1 .

Lembrando que a elipse pertence ao plano y = 0 . Show, agora vamos achar a sua normal:

∂ φ ∂ r = cos ⁡ θ , 0 ,   s e n   θ

∂ φ ∂ θ = - r   s e n   θ ,   0 ,   2 r cos ⁡ θ

∂ φ ∂ r × ∂ φ ∂ θ = i ^ j ^ k ^ cos ⁡ θ 0 2 s e n   θ - r   s e n   θ 0 2 r cos ⁡ θ = 0 , - 2 r , 0

Como a normal deve apontar para fora de W , para a elipse, isso significa y ≤ 0 , portanto, queremos esse vetor mesmo:

∂ φ ∂ θ × ∂ φ ∂ r = 0 , - 2 r , 0

Passo 5

Agora, vamos usar essa fórmula aqui:

∬ e   F → . n → d S = ∬ D   F → φ r , θ ∂ φ ∂ r × ∂ φ ∂ θ d r d θ

Escrevendo o campo em função da parametrização, temos:

F → φ r , θ = 1 + r cos ⁡ θ , 1 , 2 r   s e n   θ

Levando o que temos para a integral:

= ∫ 0 2 π ∫ 0 1 1 + r cos ⁡ θ , 1 , 2 r   s e n   θ . 0 , - 2 r , 0 d r d θ =

= - 2 ∫ 0 2 π ∫ 0 1 r d r d θ =

= - 2 ∫ 0 2 π r 2 2 0 1 d θ =

= - 2 2 ∫ 0 2 π d θ =

= - 2 π

Passo 6

Temos então

∬ S   F → . n →   d s = 4 π 2 - ∬ e   F → . n →   d s

∬ S   F → . n →   d s = 4 π 2 + 2 π

Resposta

4 π 2 + 2 π

Exercício Resolvido #2

Diomara – Cálculo Diferencial e Integral de Funções de Várias Variáveis – 1ªEdição – Cap 7 – Exercícios – Exercício 4

Encontre o fluxo do campo F x , y , z = ( e y + cos ⁡ y z , - 2 z y + s e n   x z , z 2 + 3 2 ) através da superfície S , orientada positivamente, união das superfícies S 1 e S 2 , onde S 1 é definida por z = 4 - 2 x 2 - y 2 , 0 ≤ z ≤ 2 , e S 2 tem equação z = 1 + x 2 + y 2 2 , 1 ≤ z ≤ 2 .

Passo 1

Se liga! O enunciado está pedindo para encontrar o fluxo. Para começarmos a resolver, podemos escrever que o fluxo, que chamaremos de ϕ , é dado por

ϕ = ∬ S F →     .     n →   d S .

Passo 2

O enunciado pede para achar o fluxo do campo através da união entre as superfícies S 1 e S 2 , ou seja, S 1 ∪ S 2 .

Outra informação importante é que a superfície S 1 é definida por

  z = 4 - 2 x 2 - y 2  

que representa um paraboloide elíptico com concavidade para baixo com vértice localizado no ponto ( 0,0 , 4 ). Como ele está definido em 0 ≤ z ≤ 2 , podemos esboçar o desenho dele da seguinte forma.

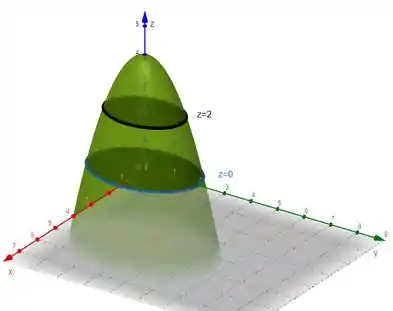
Agora podemos analisar o que acontece quando z = 0 ,

0 = 4 - 2 x 2 - y 2

x 2 2 + y 2 4 = 1 .

Chamaremos a superfície deste disco como S A .

Sendo assim, quando y = 0 temos que

x = ± 2

E para x = 0

y = ± 2 .

Assim temos duas superfícies que delimitam o sólido em z = 0 e z = 2 .

Passo 3

Se considerarmos o plano onde z = 2 , temos que

2 = 4 - 2 x 2 - y 2

x 2 + y 2 2 = 1             ( 1 )

Assim, quando y = 0 ,

x = ± 1

e para x = 0

y = ± 2 .

Passo 4

A superfície S 2 é definida por

z = 1 + x 2 + y 2 2

no intervalo 1 ≤ z ≤ 2 . Assim podemos esboçar o desenho

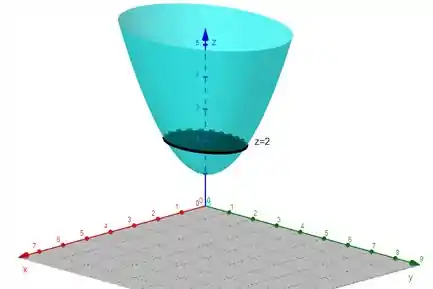
Se liga que quando z = 1

1 = 1 + x 2 + y 2 2

x 2 = - y 2 2 ⇒ x = y = 0 .

Passo 5

Analisando quando z = 2 , temos

2 = 1 + x 2 + y 2 2

x 2 + y 2 2 = 1

Repare que esta é a mesma equação (1) encontrada para a superfície S 1 quando z = 2 .

Passo 6

Se liga! Quando é feita a união das superfícies, S 1 e S 2 , no intervalo definido por

1 ≤ z ≤ 2

a superfície S 2 fica por dentro da superfície S 1 , sendo assim, quando fazemos

S = S 1 ∪ S 2

não incluímos a borda superior, quando z = 2 , da superfície S 1 . Repare que S A não está inclusa em S .

Passo 7

Considerando que temos uma superfície fechada, podemos aplicar o Teorema de Gauss.

∬ S F →     .   n →   d s = ∭ W d i v F → d V     ( 2 )

Onde

d i v   F → = ∂ F 1 ∂ x + ∂ F 2 ∂ y + ∂ F 3 ∂ z .

Fazendo as derivadas parciais, temos

∂ F 1 ∂ x = ∂ ∂ x e y + cos ⁡ y z = 0

∂ F 2 ∂ y = ∂ ∂ y - 2 z y + s e n   x z = - 2 z

∂ F 3 ∂ z = ∂ ∂ z z 2 + 3 2 = + 2 z

⇒ d i v   F → = 0 - 2 z + 2 z = 0         ( 3 )

Passo 8

Podemos separar

∬ S F →     .   n →   d s

Em

∬ S A F →     .   n →   d s + ∬ S F →     .   n →   d s       ( 4 )

Substituindo a (4) em, (2) e usando a equação (3), temos

∭ W d i v F → d V = ∬ S A F →     .   n →   d s + ∬ S F →     .   n →   d s = 0

⇒ ∬ S A F →     .   n →   d s = - ∬ S F →     .   n →   d s .     ( 5 )

Passo 9

Agora vamos fazer a parametrização de S A .

Lembrando que a superfície S A é definida por

D = x , y | x 2 2 + y 2 4 ≤ 1

E para z = 0 ,

F = x , y , 0 = e y + 1 ,       0     , 3 2 .

No exterior do sólido, temos

n A → = ( 0,0 , - 1 )

Pois aponta para fora.

Como temos todos os elementos necessários, podemos montar a integral

∬ S A F →     .   n →   d s = ∬ D e y + 1 ,       0     , 3 2 . 0,0 , - 1 d x d y

= - 3 2 ∬ D d x d y

Esta integral é a própria área da superfície S A , que é uma elipse de raios 2 e 2 . Portanto

∬ D d x d y = 2   2   π

Portanto

∬ S A F →     .   n →   d s = - 3 2 2   2   π = - 6 π .

Passo 10

Agora só precisamos substituir o valor obtido na equação (5). Sendo assim, o fluxo através da superfície S é

∬ S B F →     .   n →   d s = 6 π .

Resposta

∬ S B F →     .   n →   d s = 6 π .

Exercício Resolvido #3

Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, pp. 306-2.

Calcule ∬ S F ⋅ n d S , onde F x   , y ,   z = ( x ,   - 2 y + e x c o s z ,   z + x 2 ) e S   é definida por:

z = 9 - x 2 + y 2     ,               0 ≤ z ≤ 5 z = 5     ,                                       1 ≤ x 2 + y 2 ≤ 4 z = 8 - 3 x 2 + y 2   ,       x 2 + y 2 ≤ 1

Com campo de vetores normais exterior a S .

Passo 1

Vamos fazer um desenho da imagem somente para entender melhor o problema!

Fica mais fácil de visualizar o que precisamos fazer!

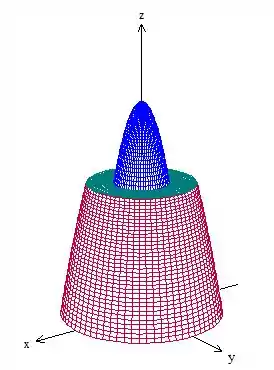
Passo 2

A superfície S não inclui a base do sólido, o disco x 2 + y 2 ≤ 9 com a normal desta base apontando para fora do sólido, ou seja, na direção negativa do eixo z . Logo, teremos,

∬ S 1   F → . n →   d S + ∬ S   F → . n →   d S = ∭ W   ∇ ⋅ F →   d V

Onde, W é o sólido fechado, S 1 é a “tampa” do sólido e ∂ W é a superfície original. Vamos começar calculando o divergente do campo:

∇ ⋅ F =   ∂ F 1 ∂ x +   ∂ F 2 ∂ y + ∂ F 3 ∂ z

∇ ⋅ F = 1 + - 2 + 1 = 0

Assim,

∭ W   ∇ ⋅ F →   d V = 0

Passo 3

Desta forma, pelo Teorema de Gauss, temos:

∬ S 1   F → . n →   d S + ∬ S   F → . n →   d S = 0

∬ S   F → . n →   d S =   - ∬ S 1   F → . n →   d S

Ou seja, para calcular o que pede o enunciado, basta calcular o fluxo que passa pela base. A base é o plano x y limitado pela circunferência x 2 + y 2 ≤ 9 .

Passo 4

Parametrizando a base, temos:

φ x ,   y = ( x ,   y ,   0 )

Como a normal de uma parametrização explícita é:

n → = - ∂ f ∂ x   , - ∂ f ∂ y ,   1

Para a orientação no sentido negativo de z ,

n → = 0   , 0 ,   - 1

Passo 5

Assim, podemos calcular o fluxo na base do sólido,

∬ S 1   F → . n →   d S =   ∬ S 1   x ,   - 2 y + e x c o s z ,   z + x 2 ⋅ 0 ,   0 ,   - 1 d x d y

∬ S 1   F → . n →   d S =   ∬ S 1   - x 2 d x d y

Para resolver esta integral, vamos usar as coordenadas polares,

x = r c o s θ y = r s e n θ

∬ S 1   F → . n →   d S = ∫ 0 2 π ∫ 0 3 ( - r 2 cos 2 ⁡ θ ) r d r d θ =   ∫ 0 2 π ∫ 0 3 ( - r 3 cos 2 ⁡ θ ) d r d θ

∬ S 1   F → . n →   d S = ∫ 0 2 π cos 2 ⁡ θ - r 4 4 0 3 d θ =   - 81 4 ∫ 0 2 π cos 2 ⁡ θ d θ

∬ S 1   F → . n →   d S = - 81 4 ∫ 0 2 π 1 + c o s 2 θ 2 d θ  

∬ S 1   F → . n →   d S =   - 81 4 θ 2 + s e n 2 θ 4 0 2 π =   - 81 4 ⋅ 2 π 2

∬ S 1   F → . n →   d S =   - 81 π 4

Resposta

Assim, o fluxo

∬ S   F → . n →   d S =   - ∬ S 1   F → . n →   d S

∬ S   F → . n →   d S = 81 π 4

Exercício Resolvido #4

Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, pp. 307-9.

Considere a superfície S obtida girando-se o segmento de reta que liga os pontos ( 1,0 , 1 ) e ( 0,0 , 3 ) em torno do eixo z . Calcule:

∬ S   r o t F → ∙ n → d S

Onde n é o campo dos vetores normais exterior a S e F é um campo vetorial em R 3 definido por:

F → = - y 3 3 + z e x , x 3 3 - cos ⁡ y z , x y

Passo 1

Reparando que os pontos estão ambos no plano y = 0   ( x z ) , desenhamos a superfície:

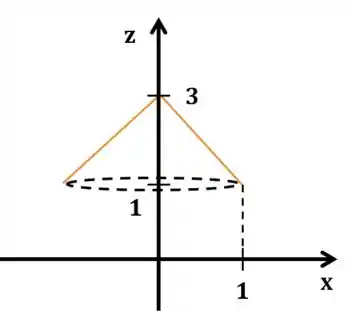
Podemos fecha-la por uma tampa S ' , tal que fechemos o sólido W . S ' é definida por:

x 2 + y 2 ≤ 1

z = 1

Passo 2

Calculando o rotacional do campo:

r o t F → = i j k ∂ ∂ x ∂ ∂ y ∂ ∂ z - y 3 3 + z e x x 3 3 - cos ⁡ y z x y = x - y s e n y z , e x - y , x 2 + y 2

Passo 3

Pelo Teorema de Gauss, sabemos que:

∬ ∂ W   r o t F → ∙ n → d S = ∬ s   r o t F → ∙ n → d S + ∬ b a s e   r o t F → ∙ n → d S = ∭ W   d i v r o t F → d W

Calculando o divergente de r o t ( F ) :

d i v r o t F → = 1 - 1 + 0

d i v r o t F → = 0

∬ s   r o t F → ∙ n → d S + ∬ b a s e   r o t F → ∙ n → d S = ∭ W   0 × d W

∬ s   r o t F → ∙ n → d S + ∬ b a s e   r o t F → ∙ n → d S = 0

∬ s   r o t F → ∙ n → d S = - ∬ b a s e   r o t F → ∙ n → d S

Passo 4

Para calcular a integral nova, fazemos uma parametrização da superfície que é a base:

ϕ t , θ = t cos ⁡ θ , t   s e n θ , 1

θ ∈ 0,2 π

t ∈ 0,1

Achando o vetor normal:

n → = ∂ ϕ ∂ t × ∂ ϕ ∂ θ

n → = i j k cos ⁡ θ s e n θ 0 - t   s e n θ t cos ⁡ θ 0

n → = 0,0 , t

Que está apontando para dentro da superfície, como vemos no desenho, portanto trocamos o sinal para respeitar o enunciado e ter um vetor normal exterior:

n → = 0,0 , - t

Passo 5

Substituindo a parametrização na equação de campo e sabendo que a primeira e a segunda coordenadas não influem em nada pois o produto escalar com o normal vai zerar elas:

r o t F → = x - y s e n y z , e x - y , x 2 + y 2

r o t ( F → ) = ( ? , ? , t 2 )

r o t ( F → ) ∙ n → = 0 + 0 - t 3

r o t ( F → ) ∙ n = - t 3

Substituindo na fórmula, juntamente com os limites de integração da parametrização:

I = - ∫ 0 2 π ∫ 0 1 t 3 d t d θ

I = - 2 π t 4 4 0 1

I = - 2 π × 1 4

I = - π 2

Substituindo na integral que queríamos:

∬ s   r o t F → ∙ n → d S = - ∬ b a s e   r o t F → ∙ n → d S

∬ s   r o t F → ∙ n → d S = - - π 2

Resposta

∬ s   r o t F → ∙ n → d S = π 2

Exercício Resolvido #5

UFRJ - Cálculo 3 - P2 2012.2 - 4

Seja S a porção da esfera: x 2 + y 2 + z 2 = 1

Compreendida entre os planos z = 0 e z = y , com y ≥ 0 . Calcular: K = ∬ S   F ∙ n →   d S

Onde n → é a normal unitária a S cuja terceira coordenada é sempre positiva e F é definido por:

F = ln ⁡ 1 + y 2 2 + cos ⁡ z , 1,2 z

Passo 1

É claro que se trata de uma questão de Teorema de Gauss pois a expressão do campo vetorial é complicada demais para se fazer a integral de superfície. Aplicando:

∬ S   F ∙ n →   d S = ∭ W   d i v ( F ) d x d y d z

Onde a superfície S deve encerrar o volume W . Dessa forma, temos a superfície composta pela porção da esfera e dois planos, o z = 0 e o z = y :

S = E ∪ P 1 ∪ P 2

Calculando o divergente:

d i v F = 2

Passo 2

Substituindo na fórmula:

∬ S   F ∙ n →   d S = ∭ W   2   d x d y d z

Agora precisamos enxergar nossa região W . Fazendo um corte da esfera em y z , obtemos um círculo de raio 1 e a reta z = y .

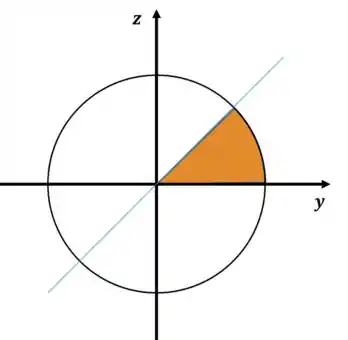
Podemos ver que a região em questão é um oitavo da esfera, portanto:

∬ S   F ∙ n →   d S = 2 ∭ W   d x d y d z

∬ S   F ∙ n →   d S = 2 × 1 8 4 3 π × 1 3

∬ S   F ∙ n →   d S = π 3

Passo 3

Agora precisamos separar a integral da região S para calcularmos o fluxo que queremos. Temos que, como:

S = E ∪ P 1 ∪ P 2

É válida a relação:

∬ S   F ∙ n →   d S = ∬ E   F ∙ n →   d S + ∬ P 1   F ∙ n →   d S + ∬ P 2   F ∙ n →   d S

Como o que é pedido pelo enunciado é o fluxo pela porção da esfera, então vamos calcular os outros dois e isolar este. Vamos encontrar os conjuntos que representam os planos. Temos que para o primeiro:

z = 0

Substituindo na equação da esfera, temos a fronteira da região:

x 2 + y 2 + 0 2 = 1

x 2 + y 2 = 1

Portanto, aliado ao fato de que y ≥ 0 , temos o conjunto do primeiro plano:

P 1 = x , y , z ∈ R 3 x 2 + y 2 ≤ 1 ,     z = 0 ,     y ≥ 0

Que possui vetor normal:

n → = ( 0,0 , - 1 )

Pelo macete dos vetores normais do plano. Calculando o fluxo:

∬ P 1   F ∙ n →   d S = ∬ P 1   … , … , 2 × 0 ∙ 0,0 , - 1   d S

∬ P 1   F ∙ n →   d S = 0

Note que as componentes x e y do campo vetorial não importam pois o vetor normal as zeraria.

Passo 4

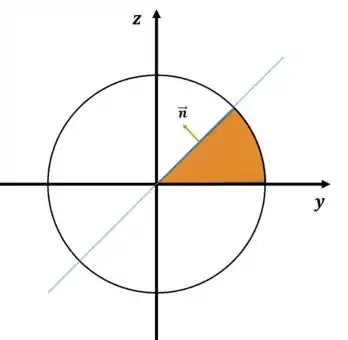
Fazendo a mesma lógica para o segundo plano, temos que:

z = y

Substituindo na equação da esfera, temos a fronteira da região:

x 2 + y 2 + y 2 = 1

x 2 + 2 y 2 = 1

Logo, podemos parametrizar o segundo plano de forma explícita como abaixo

φ x , y = { x , y , y , x , y ∈ x 2 + 2 y 2 ≤ 1 ( D ) }

Então, os vetores normais serão do tipo

z - y = 0 → n → = 0 , - 1,1

Pode conferir que ele aponta para fora do sólido, conforme exigido no enunciado:

Por fim fazemos a maldita conta, não esquecendo de substituir a condição z = y :

∬ P 1   F ∙ n →   d S = ∬ D   ( … , 1,2 y ) ∙ 0 , - 1,1   d x d y

Que segue:

∬ D   ( 2 y - 1 ) d x d y

E agora nos resta uma conta chata em coordenadas polares.

Passo 5

Agora para fazer a integral dupla, vamos passar para coordenadas polares

x = r cos ⁡ θ

y = 2 2 r sen ⁡ θ

De onde tiramos o novo domínio em coordenadas polares:

r 2 ≤ 1 → 0 ≤ r ≤ 1

y ≥ 0 → 2 2 r sen ⁡ θ ≥ 0 → sen ⁡ θ ≥ 0

0 ≤ θ ≤ π

Passo 6

Substituindo tudo, junto com o domínio e etc:

2 2 ∫ 0 π ∫ 0 1 2 r sen ⁡ θ - 1 r d r d θ

Agora é papo de fazer conta:

2 2 ∫ 0 π 2 3 sen ⁡ θ - 1 2 d θ

2 2 2 2 3 - π 2

Logo, temos que:

∬ S   F ∙ n →   d S = ∬ E   F ∙ n →   d S + ∬ P 1   F ∙ n →   d S + ∬ P 2   F ∙ n →   d S

Basta substituir todos os valores:

π 3 = ∬ E   F ∙ n →   d S + 0 + 2 2 2 2 3 - π 2

Isolando:

∬ E   F ∙ n →   d S = π 3 - 2 2 2 2 3 - π 2

Voilá! Chato. Para. Caraleo. Mas faz parte, né...

Resposta

∬ E   F ∙ n →   d S = π 3 - 2 2 2 2 3 - π 2