Reta Normal e Plano Tangente
Produzido por Arthur Melo de AlmeidaTeoria
Gráfico de Superfícies
Aqui vamos aprender a pegar a parametrização da superfície e achar o seu gráfico!
Lembra de como conferimos se as parametrizações cilíndricas e esféricas estavam corretas?! Se não lembra não tem problema! Vamos ver aqui de novo!
Esse é um tipo totalmente prático! Então alguns exemplos vão ajudar mais do que explicações genéricas!
Exemplo: Seja a equação parametrizada , vamos encontrar sua equação explícita! Mas como começo um problema desses?!
Organizar as variáveis é um bom começo!
Agora temos que encontrar uma maneira de relacionar e . Neste caso, uma maneira de se fazer é isolar os parâmetros em função de qualquer uma das variáveis e substituir na outra! Sei que não ficou muito claro! Rs
Mas na prática é mais simples, olhe:
A única variável que não usamos foi ! Então o que acha de substituir e na equação do ?! Vamos ver se é uma boa ideia:
Já deu pra notar que não temos mais e na expressão? Então, agora é legal reorganizar o que encontramos!
Temos uma equação explícita que representa um plano!
Exemplo: Este exemplo é um caso diferente e mais complicado que o anterior. Temos a seguinte equação paramétrica:
O início é parecido com o exemplo anterior, então vamos começar organizando as variáveis:
No exemplo anterior deixamos os parâmetros em função de duas variáveis e substituímos na terceira. Neste caso fica difícil isolar em função de alguma variável.... Não desanime! Vamos relembrar uma relação importante que vimos no tipo anterior!
A relação fundamental da trigonometria! Então, temos que:
Mas conhecemos os valores de e , não?!
Substituindo na relação fundamental temos:
Hum.... Mas ainda temos o parâmetro na nossa equação. Olhando as variáveis vemos que , então vamos substituir e ver no que dá!
Reorganizando para ficar mais clara a superfície, temos:
Pronto! Agora já aprendemos mais uma forma de achar nossa equação cartesiana!
Macete para fazer gráficos
Agora que sabemos encontrar a equação cartesiana, para que ele vai ser útil?!
Bom, para construir um gráfico existe um macete que funciona melhor se a superfície estiver na sua forma explícita!
A dica é: Zerar uma variável de cada vez!
Vamos ver um exemplo para ajudar!
Exemplo: Construa o gráfico da equação
Vamos começar vendo o que acontece quando fazemos , a equação fica que é uma parábola com vértice na origem no plano , veja:
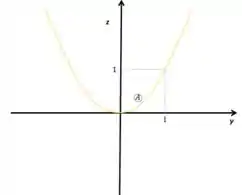
Agora vamos fazer , então temos , que da mesma forma teremos uma parábola com vértice na origem e no plano , veja:
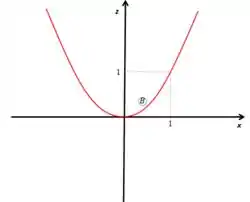
Por fim, fazendo , temos que que somente ocorre na origem! Então a interseção da superfície com o plano é um ponto, mais especificamente a origem.
Agora que vimos a interseção de cada plano com a superfície fica mais fácil de desenhá-la! Olha o resultado final:
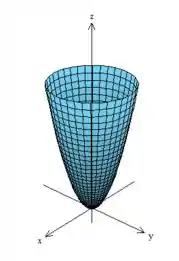
Reta Normal e Plano Tangente
Já sabemos parametrizar superfícies de forma explicita, avançada, etc. Para começarmos a integrar superfícies pra valer, vamos precisar acrescentar esse novo conteúdo: a reta normal e o plano tangente à superfície.
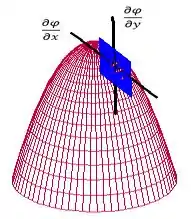
Dada uma superfície qualquer, para cada ponto dela vai existir um plano tangente e um vetor normal. Vê, por exemplo, esse paraboloide , no ponto somente existe esse plano tangente (azul) e esse vetor normal (preto):

Perceba que os conceitos de plano tangente e vetor normal estão associados, certo? O plano tangente é mais fácil de enxergar, é aquela história de somente “encostar” em um ponto na superfície. O vetor normal vai ser aquele perpendicular a esse plano que criamos. Meio abstrato demais? Vamos colocar umas contas, então!
Exemplo
Beleza, como calculamos isso? Primeiro vamos precisar de uma parametrização da superfície, no caso, o nosso paraboloide. A parametrização explícita vai ser essa aqui:
Para achar o vetor normal, sempre vamos precisar derivar nossa superfície em relação aos dois parâmetros de forma independente, assim, olha:
A nossa primeira derivada, naquele ponto , graficamente pertence ao plano tangente! Fica assim:
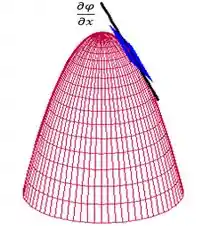
A segunda derivada também vai pertencer ao plano tangente! Fica assim:
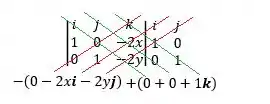
Po, se temos dois vetores que pertencem ao plano tangente, podemos descobrir a equação do seu vetor normal e, consequentemente, descobrir a equação do plano! Pra isso, faremos o produto vetorial entre essas duas derivadas:
Lembra como resolve esse determinante? A gente repete as duas primeiras colunas e depois multiplica tudo cruzado:
Essa é a normal em qualquer ponto do paraboloide! Geralmente a questão vai te pedir a normal em um ponto específico. Não tem problema, é só substituir os valores! No nosso exemplo:
Tendo a normal e o ponto , encontrar a equação do plano é simples: usamos essa equação aqui:
A equaç��o da reta normal é essa aqui embaixo
No nosso caso, vamos ter:
Macete – Parametrização Explícita
Quando temos a parametrização explícita, ou seja, , existe uma fórmula que dá direto o nosso vetor normal!
No nosso exemplo do paraboloide,
Na fórmula do nosso macete:
Vê se não deu igual ao resultado que achamos fazer toda aquela conta!

Simples né, mas cuidado! Não é sempre que a parametrização explícita é fácil, mas quando o problema já te dá uma parametrização explícita pode usar isso aí!
Pra fechar esse tipo de exercício, vamos fazer um passo a passo de como encontrar a equação da reta normal e do plano tangente à superfície:
Passo 1: Encontrar a parametrização da superfície
Passo 2: Derivar a superfície em relação aos dois termos separadamente
Passo 3: Calcular o vetor normal pelo produto vetorial das duas derivadas
Passo 4: Encontrar a parametrização da reta normal – e – a partir do ponto e do vetor
Passo 5: Obter a equação do plano tangente pelo produto escalar:
Macete para fazer gráficos
Reta Normal e Plano Tangente
Exemplo
Macete – Parametrização Explícita
Exercícios Resolvidos
Exercício Resolvido #1
Hamilton Luiz Guidorizzi, Um curso de Cálculo – volume 3, 3ª ed. Rio de Janeiro: LTC, 1997, pp. 208 – 1c
Desenhe a imagem da superfície parametrizada dada por
Passo 1
Vamos encontrar a equação da superfície não parametrizada, assim, devemos fazer as substituições:
Passo 2
Substituindo os valores de na expressão do a gente vai ter isso aqui
Passo 3
Temos que a imagem é um plano que é delimitado pelas desigualdades previstas no enunciado.
Que passando para as variáveis , e temos:
Agora a última desigualdade a gente pode fazer o seguinte
Passo 4
A imagem da superfície parametrizada será:
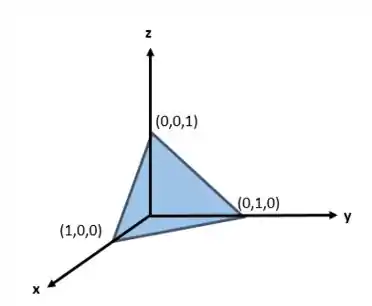
Resposta
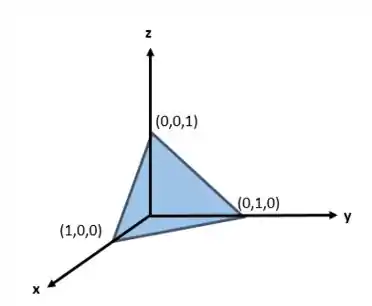
Exercício Resolvido #2
PUC-RJ - Cálculo 3 - P3 2014.1 - 2a
Quais superfícies dadas na figura abaixo correspondem às parametrizações II e IV:
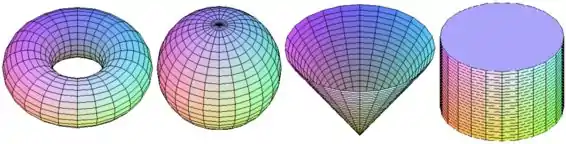
Passo 1
Vamos olhar as parametrizações de e , primeiro com
Repara que temos
Então
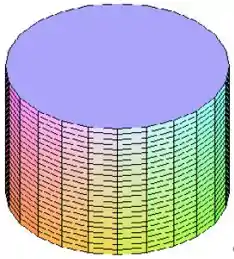
Isso é uma circunferência, e ela independe do valor de , ou seja, ela vai ficar sendo repetida para cada valor de entre e , e a figura que fica assim é o cilindro, ou seja, a quarta figura.
Passo 2
Vamos olhar agora a parametrização de
Aqui se temos um seno e cosseno de novo, fazemos e vamos ter
Dessa vez sobrou aquele , mas isso é na nossa parametrização, então vamos ter
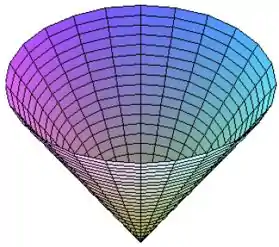
E essa equação é de um cone, e dentro das figuras o cone é a terceira figura.
Resposta
Exercício Resolvido #3
Elaboração Própria
Encontre a equação da reta normal e do plano tangente à superfície parametrizada por no ponto
Passo 1
Equação da reta normal e plano tangente né? Sabemos que precisamos encontrar o vetor normal para poder descobrir o que o enunciado pede, para isso vamos usar aquela fórmula:
Ou então usamos aquele macete da parametrização explícita! Isso vai de cada um, nesse primeiro exercício vamos fazer os dois pra deixar claro como é, a partir do próximo vamos escolher o que for mais simples!
Depois que acharmos a normal com o , nossa parametrização da reta normal vai ser:
Em seguida, para calcular a equação do plano, vamos usar o produto escalar da teoria também, se você não lembra é esse aqui:
Vamos lá?
Passo 2
Calculando a normal pelo produto vetorial, vamos precisar derivar a superfície em e :
Para calcular a normal pelo macete, usamos essa fórmula aqui, sendo a parametrização explícita em :
No nosso caso as variáveis são e , mas não faz diferença, podemos usar a mesma fórmula:
Temos a equação do vetor normal em qualquer ponto, certo? Mas só precisamos do valor dele no ponto . Como e , esse ponto é o ponto em que e . Assim,
Passo 3
Tendo o nosso vetor normal, podemos agora encontrar a parametrização da reta normal à superfície. Para isso vamos usar aquele conceito escrito no passo 1.
Passo 4
Para encontrar a equação do plano, precisamos calcular o produto escalar escrito no primeiro passo:
Resposta
Exercício Resolvido #4
Elaboração Própria
Encontre a parametrização da reta normal e o plano tangente à superfície parametrizada por no ponto em que e
Passo 1
Parametrização da reta normal e plano tangente, quando lemos isso já tem que vir na nossa cabeça que precisamos encontrar o vetor normal no ponto dado.
Nessa questão a nossa parametrização não é explicita, vamos precisar usar essa fórmula de cima mesmo. Além disso, não temos o ponto , temos o valor dos parâmetros nesse ponto, certo? Não tem problema, só precisamos substituir e na parametrização da superfície!
Então pronto, depois que acharmos e conseguimos calcular a parametrização da reta normal e a equação do plano tangente! Vamos lá?
Passo 2
Vamos começar pelo vetor normal, precisamos derivar a nossa parametrização da superfície em relação aos seus dois parâmetros. Fica assim:
Nosso vetor normal vai ser:
Se não temos termo em , quer dizer que a coordenada do vetor no eixo é igual a zero! Portanto:
Esse é o vetor normal em qualquer ponto, né? Precisamos do valor dele no ponto em que
Substituindo esses valores:
Passo 3
Precisamos encontrar o nosso ponto que o enunciado fala, ele diz que o ponto é definido por:
Mas a nossa parametrização não é exatamente a descrição de todos os pontos da superfície? Então basta substituir os valores dos parâmetros na equação da parametrização:
Passo 4
Tendo o vetor normal e o ponto podemos encontrar o valor da parametrização da reta normal da seguinte forma:
Substituindo nossos valores:
Passo 5
E, para calcular a equação do plano, precisamos do seguinte produto escalar:
Simplificando, dividindo os dois lados por :
Resposta
Exercício Resolvido #5
Elaboração Própria
Encontre a equação da reta normal e do plano tangente ao cone no ponto
Passo 1
Essa questão aqui vai dar um pouco mais de trabalho porque vamos ter que encontrar a parametrização do cone, depois que fizermos isso, é só seguir os mesmos passos que estávamos fazendo: encontrar o vetor normal , encontrar a reta normal e o plano tangente.
Vamos começar parametrizando a nossa superfície. Podemos fazer a parametrização explícita, para usar o macete, ou parametrizar de alguma outra forma, isso vai de cada pessoa. Nesse caso, a parametrização explícita já está pronta pra gente, vamos usá-la então:
Passo 2
Vamos encontrar agora o nosso vetor normal, pelo macete, sabemos que:
Vamos calcular então as derivadas de em relação a e a :
Esse é o vetor normal para qualquer ponto, né? Queremos saber o valor desse vetor no ponto dado no enunciado , substituindo e nos termos da normal:
Passo 3
Temos o vetor normal e o ponto , podemos agora achar a parametrização da reta normal! Para isso, vamos substituir os valores nessas fórmulas aqui:
No nosso exercício:
Passo 4
Para encontrarmos a equação do plano tangente, vamos precisar fazer o produto escalar entre o vetor normal e aquele termo lá da teoria, lembra? Isso aqui:
Pronto! Encontramos a reta normal e o plano tangente!