- Se , encontre
- Verifique se sua resposta na parte (a) foi razoável comparando os gráficos de e .
Passo 1
Olá, meu nobre estudante. Pronto para mais uma resolução?
Então, aqui a gente tem uma função:
E iremos encontrar a sua derivada.
Para isso, vamos utilizar a fórmula:
Para que a gente consiga ver se estamos certos no nosso cálculo da revidada, iremos comparar o gráfico de e .
Passo 2
- Pela definição, sabemos que
- Esboçando os gráficos utilizando o GeoGebra:
Onde:
E
Então vamos substituir:
Realizando o produto notável:
Simplificando os termos semelhantes:
Simplificando os dois primeiros termos por terem :
Calculando o limite do primeiro termo, e multiplicando o segundo termo pelo conjugado, para que assim a gente consiga simplificar o :
Realizando o produto:
Simplificando:
Finalmente calculando o limite:
Encontramos então nossa derivada.
Passo 3
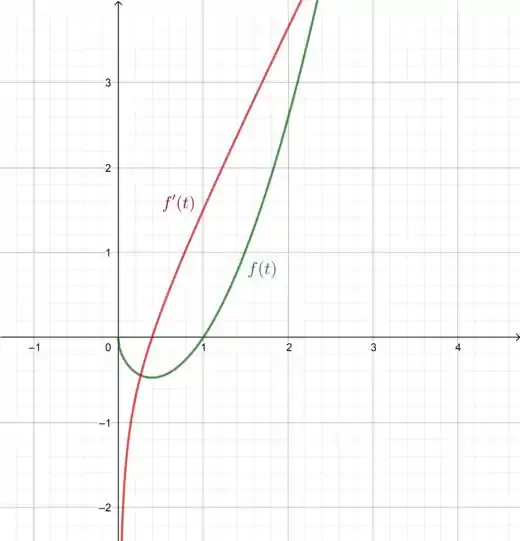
Quando está próximo de ,
também está próximo de ,
então
é muito grande e isso corresponde às retas tangentes íngremes perto de . Pois lembre-se que a derivada é a inclinação da reta tangente no ponto dado.
parece razoável como a derivada de
Resposta
- Em comparação com o gráfico a aproximação foi razoável