Exercícios de Definição de Derivadas - Lista de Exercícios Resolvida
Questão 1
- Quando uma função é derivável no ponto ?
Dê a definição
- Usando a definição dada no item , calcule a derivada da função
Dê a definição
No ponto .
Ver solução completaQuestão 2
Use a definição para calcular as derivadas da função. Depois, determine os valores da derivada conforme especificado.
Ver solução completaQuestão 5
Mostre, através da definição da derivada, que a derivada de um polinômio é:
Ver solução completaQuestão 6
Para cada uma das seguintes funçōes, calcule pela definição a sua função derivada:
h)
Ver solução completaQuestão 7
- Em cada item abaixo, calcule a derivada da função no ponto indicado.
b. e
Ver solução completaQuestão 9
Use a definição de derivada para calcular a derivada de . Determine o domínio de .
Ver solução completaQuestão 10
8 – Se a posição de um carro no instante é dada por , então a sua velocidade pode ser calculada a partir do seguinte limite
Calcule a velocidade em cada um dos casos abaixo.
a)
Ver solução completaQuestão 11
Seja uma função contínua satisfazendo as seguintes propriedades:
- e
- é derivável até segunda ordem em ;
- Existe uma função contínua tal que para todo e
- Existe uma função contínua tal que para todo e
(a) Usando a Regra de L’Hospital para calcular o limite, decida se é derivável em e determine, em caso afirmativo, .
(b) Estude f em relação a seus intervalos de crescimento e decrescimento, intervalos de concavidade, pontos de máximo e mínimo locais e globais e pontos de inflexão.
(c) Esboce o gráfico de .
Ver solução completaQuestão 12
Seja uma função contínua derivável satisfazendo as seguintes propriedades:
- ;
- ;
Considere também que a função definida por . Decida se cada afirmação é verdadeira ou falsa:
A) A equação possui exatamente uma solução real. A solução dessa equação é um número real estritamente positivo.
B) A equação possui exatamente duas soluções reais.
C) A função possui um único ponto de mínimo local.
D) A função possui ao menos um ponto de máximo local.
E) A equação possui ao menos uma solução real.
Ver solução completaQuestão 13
Um triângulo possui dois de seus lados iguais a 3cm e 8cm e o terceiro lado variando com o tempo. Em um certo instante, o lado mede 7cm e está aumentando a uma taxa de . Determine a taxa com a qual o ângulo oposto ao lado está variando neste momento.
Ver solução completaQuestão 14
Considere todos os triângulos retângulos cujos catetos estão contidos nos eixos coordenadas e que a hipotenusa contém o ponto (3,2). A menor área que um desses triângulos pode ter é quanto?
Ver solução completaQuestão 15
Seja uma função derivável tal que . Suponha que seja duas vezes derivável em e que . Suponha ainda que se . O valor do limite
É:
Ver solução completaQuestão 18
Use a definição de derivada de uma função para calcular e determine a equação da reta tangente ao gráfico da função no ponto
Ver solução completaQuestão 19
Considere as funções e , onde são constantes reais e . Decida a veracidade das afirmações abaixo:
- Se , então é estritamente crescente
- Se , então possui exatamente um ponto de máximo e um ponto de mínimo local
- Se , então possui um único ponto crítico que não é ponto de máximo ou mínimo local
- Se , então é estritamente decrescente
- A derivada de é uma função limitada
- Se , então é estritamente crescente
- e , então possui exatamente um ponto de máximo e um ponto de mínimo local
- Se , então possui um único ponto crítico que não é ponto de máximo ou mínimo local
- Se , então é estritamente decrescente
- A derivada de é uma função limitada
Passo 1
E aí, galerinha! Tudo na paz por aí?
Vamos aqui ter que avaliar uma por uma das alternativas e usando a teoria que conhecemos, aplicar nossos conhecimentos e ver se são verdadeiras ou falsas. O enunciado não pede, mas vamos justificar todas elas pra gente ter sempre uma ideia do que estamos fazendo.
Passo 2
Falsa, pois se então . Logo, não pode ser estritamente crescente.
Verdadeira. Agora tem duas raízes, sendo negativa somente no intervalo entre essas raízes. Uma análise do crescimente da função garante o resultado.
Verdadeira. Aproveitando até o que discutimos anteriormente, a condição garante que (uma única raiz dupla) e portanto, sempre crescente, com um único ponto crítico.
Falsa, pois tem discriminante que, se negativo garante para todo , logo é estritamente crescente.
Verdadeira, pois e portanto,
Ver solução completaQuestão 21
03) Use a definição de derivada de uma função para calcular e determine a equação da reta tangente ao gráfico da função no ponto .
Ver solução completaQuestão 22
01) Use a definição de derivada de uma função para calcular e determine a equação da reta tangente ao gráfico da função no ponto .
Ver solução completaQuestão 23
02) Use a definição de derivada de uma função para calcular e determine a equação da reta tangente ao gráfico da função no ponto .
Ver solução completaQuestão 25
- Em cada item abaixo, calcule a derivada da função no ponto indicado.
h. e
Ver solução completaQuestão 26
- Em cada item abaixo, calcule a derivada da função no ponto indicado.
g. e
Ver solução completaQuestão 27
- Em cada item abaixo, calcule a derivada da função no ponto indicado.
f. e
Ver solução completaQuestão 28
Use a definição derivada para calcular a derivada de cada uma das funções no
ponto indicado:
no ponto
Ver solução completaQuestão 29
Use a definição de derivada de uma função para calcular e determine a equação da reta tangente ao gráfico da função no ponto
Ver solução completaQuestão 30
Use a definição derivada para calcular a derivada de cada uma das funções no
ponto indicado:
no ponto
Ver solução completaQuestão 31
Use a definição derivada para calcular a derivada de cada uma das funções no
ponto indicado:
no ponto
Ver solução completaQuestão 32
- Em cada item abaixo, calcule a derivada da função no ponto indicado.
e. e
Ver solução completaQuestão 33
Com a definição de derivada e as propriedades de limite, calcule para:
Ver solução completaQuestão 34
Considere a função:
Usando a definição de derivada, calcule . Aqui, é um número real qualquer.
Ver solução completaQuestão 37
- Em cada item abaixo, calcule a derivada da função no ponto indicado.
l. e
Ver solução completaQuestão 38
Para que o Teorema de Weierstrass possa ser aplicado, é necessário que a função seja diferenciavel no intervalo considerado?
Ver solução completaQuestão 39
3. Dois objetos e movem-se sobre uma linha reta e suas posições em função do tempo são dadas, respectivamente, por e , sendo as posições medidas em metros e o tempo em segundos.
(a) Determine as posições iniciais dos objetos, em .
(b) Determine as posições dos objetos, em .
(c) Determine as velocidades médias dos objetos entre os instantes e .
(d) Determine as velocidades dos objetos no instante .
(e) Determine as velocidades dos objetos no instante .
(f) Em qual instante de tempo entre e os dois objetos possuem a mesma velocidade?
Ver solução completaQuestão 40
Considere a curva definida pela equação . Calcule e encontre uma equação da reta tangente à curva no ponto .
Ver solução completaQuestão 41
Suponha que para todo . Considere as seguintes afirmações:
- é contínua em .
- é diferenciável em .
- .
É verdadeira ou são verdadeiras:
- Todas as três afirmativas.
- Somente a afirmativa (II).
- Somente a afirmativa (I).
- Nenhuma das afirmativas.
- As afirmativas (I) e (II).
Questão 42
Considere uma função satisfazendo:
Então, vale necessariamente que:
- .
- não existe.
- não está definida em .
- .
Questão 43
Para as seguintes funções calcule a derivada no ponto indicado através do limite do quociente de Newton:
Questão 44
Para as seguintes funções calcule a derivada no ponto indicado através do limite do quociente de Newton:
Questão 45
Para as seguintes funções calcule a derivada no ponto indicado através do limite do quociente de Newton:
Questão 47
Questão 4:
Use a definição precisa de derivada (via limite) e prove que se então .
Ver solução completaQuestão 48
Calcule por meio da definição a derivada de (não é permitido aqui usar a regra de L’Hospital).
Ver solução completaQuestão 52
Considere a função definida por:
(b) Use a definição de derivada para mostrar que não é derivável em
Ver solução completaQuestão 53
(Stewart) Se uma bola for atirada ao ar com velocidade de , sua altura em metros, após segundos, é dada por . Usando derivadas, encontre a velocidade da bola quando .
Ver solução completaQuestão 54
17. Devido a sua conexão com retas secante, tangente e taxas instantâneas, os limites da forma
Ocorrem com frequência em cálculo. Avalie os seguintes limites para os valores dados de e a função .
a)
Ver solução completaQuestão 55
17. Devido a sua conexão com retas secante, tangente e taxas instantâneas, os limites da forma
Ocorrem com frequência em cálculo. Avalie os seguintes limites para os valores dados de e a função .
c)
Ver solução completaQuestão 56
17. Devido a sua conexão com retas secante, tangente e taxas instantâneas, os limites da forma
Ocorrem com frequência em cálculo. Avalie os seguintes limites para os valores dados de e a função .
d)
Ver solução completaQuestão 57
Determine a equação da reta tangente a cada curva no ponto indicado:
a) em
Ver solução completaQuestão 58
Determine a equação da reta tangente a cada curva no ponto indicado:
b) em
Ver solução completaQuestão 59
1) Sejam e duas funções tais que , , e . Sejam e funções definidas por , .
É correto afirmar que
Escolha uma:
a)
b)
c)
d)
e)
Ver solução completaQuestão 61
Determine a equação da reta tangente a cada curva no ponto indicado:
c) em
Ver solução completaQuestão 62
Determine a equação da reta tangente a cada curva no ponto indicado:
e) em
Ver solução completaQuestão 63
Para as seguintes funções calcule a derivada no ponto indicado através do limite do quociente de Newton:
Questão 64
(Stewart) Se uma pedra for lançada para cima no planeta Marte, com velocidade de , sua altura em metros, após segundos, é dada por .
c) Quando à pedra atinge a superfície?
Ver solução completaQuestão 67
Use a definição derivada para calcular a derivada de cada uma das funções no
ponto indicado:
no ponto
Ver solução completaQuestão 68
Use a definição derivada para calcular a derivada de cada uma das funções no
ponto indicado:
no ponto
Ver solução completaQuestão 69
Use a definição derivada para calcular a derivada de cada uma das funções no
ponto indicado:
no ponto
Ver solução completaQuestão 70
Use a definição derivada para calcular a derivada de cada uma das funções no
ponto indicado:
no ponto
Ver solução completaQuestão 72
- Em cada item abaixo, calcule a derivada da função no ponto indicado.
-
e
Ver solução completaQuestão 73
A posição de uma partícula sobre uma linha reta graduada em metros no instante segundos é dada por
- Determine
- Determine
- Em quais instantes a partícula está em repouso?
- Quando a partícula está se movendo para frente? E quando está se movendo para trás?
- Qual é o deslocamento da partícula entre os instantes e ?
- Qual é a distância percorrida pela partícula entre os instantes 0 e 5s?
- Para que valores de tem-se Para quais valores de tem-se Para quais valores de tem-se
- Quando a partícula está acelerando ou freando?
Questão 74
Sabemos que a velocidade de um objeto em um determinado instante é o coeficiente angular da reta que é tangente na abscissa ao gráfico da posição s(t) em função do tempo t. Com isso, definimos derivada e esta tem a mesma fórmula que usamos para o cálculo do coeficiente angular. Assim, a derivada da posição é a velocidade (em fórmula, isso fica ).
- O movimento retilíneo uniforme (MRU) é caracterizado por ser um movimento com velocidade constante. Considerando o instante inicial de movimento como , a posição inicial como e a velocidade como sendo , a fórmula que foi passada na escola para a posição do objeto é . Utilize seu conhecimento recém aprendido de derivada para mostrar que um objeto que possui a equação de movimento tem velocidade em qualquer instante (concluindo que o movimento possui, de fato, velocidade constante).
- O movimento retilíneo uniforme variado (MRUV) é caracterizado por ser um movimento com aceleração constante (nesse caso a velocidade pode variar, mas de maneira uniforme). Considerando o instante inicial de movimento como , a posição inicial como , a velocidade inicial como sendo e a aceleração como , a fórmula que foi passada na escola para a posição do objeto é e para a velocidade é . Utilize seu conhecimento recém aprendido de derivada para mostrar que um objeto que possui a equação de movimento tem velocidade (concluindo que as fórmulas para o MRUV são válidas).
Questão 75
O número de células de levedura em uma cultura de laboratório aumenta rapidamente no início, mas eventualmente estabiliza. A população é modelada pela função
Em que é medido em horas. No instante a população é de 20 células e está crescendo a uma taxa de . Encontre os valores de e . De acordo com este modelo, o que ocorre com a população de levedura depois de muito tempo?
Ver solução completaQuestão 77
(Stewart) Se uma pedra for lançada para cima no planeta Marte, com velocidade de , sua altura em metros, após segundos, é dada por .
a) Encontre a velocidade da pedra após um segundo.
Ver solução completaQuestão 78
(Stewart) Se uma pedra for lançada para cima no planeta Marte, com velocidade de , sua altura em metros, após segundos, é dada por .
b) Encontre a velocidade da pedra quando .
Ver solução completaQuestão 79
Se uma pedra for lançada pra cima no planeta Marte com uma velocidade de , sua altura (em metros) depois de segundos é dada por
- Com que velocidade a pedra atinge a superfície?
Questão 80
17. Devido a sua conexão com retas secante, tangente e taxas instantâneas, os limites da forma
Ocorrem com frequência em cálculo. Avalie os seguintes limites para os valores dados de e a função .
b)
Ver solução completaQuestão 81
Seja uma função definida em ℝ. Suponha que exista tal que, para todo ,
.
Mostre que é contínua em .
Ver solução completaQuestão 82
- Em cada item abaixo, calcule a derivada da função no ponto indicado.
i. e
Ver solução completaQuestão 85
- Em cada item abaixo, calcule a derivada da função no ponto indicado.
c. e
Ver solução completaQuestão 86
- Em cada item abaixo, calcule a derivada da função no ponto indicado.
d. e
Ver solução completaQuestão 87
- Em cada item abaixo, calcule a derivada da função no ponto indicado.
k. e
Ver solução completaQuestão 89
Em cada um dos itens abaixo, encontre a derivada da função usando a definição
(e)
Ver solução completaQuestão 90
Em cada um dos itens abaixo, encontre a derivada da função usando a definição:
c)
Ver solução completaQuestão 91
Em cada um dos itens abaixo, encontre a derivada da função usando a definição:
a)
Ver solução completaQuestão 92
Sejam um intervalo aberto e uma função. Dado , a reta tangente ao gráfico de no ponto é a (única) reta que passa pelo ponto e tem inclinação igual a
,
Ver solução completaQuestão 93
Sejam um intervalo aberto e uma função. Dado , a reta tangente ao gráfico de no ponto é a (única) reta que passa pelo ponto e tem inclinação igual a
,
Ver solução completaQuestão 94
Sejam um intervalo aberto e uma função. Dado , a reta tangente ao gráfico de no ponto é a (única) reta que passa pelo ponto e tem inclinação igual a
,
Ver solução completaQuestão 97
Um fabricante produz peças de tecido. O custo, em reais, da produção de metros de um certo tecido é .
- Qual é o significado de Qual é a unidade de
- O que significa dizer que
Questão 98
Use a definição de derivada de uma função para calcular e determine a equação da reta tangente ao gráfico da função no ponto
Questão 100
Use a definição de derivada de uma função para calcular e determine a equação da reta tangente ao gráfico da função no ponto
Questão 101
Use a definição de derivada para encontrar as funções e seu domínio:
(a)
Ver solução completaQuestão 102
Use a definição de derivada de uma função para calcular e determine a equação da reta tangente ao gráfico da função no ponto
Questão 103
Use a definição de derivada de uma função para calcular e determine a equação da reta tangente ao gráfico da função no ponto
b)
Ver solução completaQuestão 104
- Em cada item abaixo, calcule a derivada da função no ponto indicado.
h. e
Ver solução completaQuestão 106
Sejam I ⊂ R um intervalo aberto e uma função. Dado , lembre que a reta tangente ao gráfico de f no ponto é a (única) reta que passa pelo ponto e tem inclinação igual a
quando o limite existe. Neste caso, a equação da reta tangente é dada por .
Para cada uma das funções abaixo, determine a inclinação em um ponto genérico. Em seguida, calcule a equação da reta tangente no ponto indicado.
(c)
Ver solução completaQuestão 107
Sejam I ⊂ R um intervalo aberto e uma função. Dado , lembre que a reta tangente ao gráfico de f no ponto é a (única) reta que passa pelo ponto e tem inclinação igual a
quando o limite existe. Neste caso, a equação da reta tangente é dada por .
Para cada uma das funções abaixo, determine a inclinação em um ponto genérico. Em seguida, calcule a equação da reta tangente no ponto indicado.
(a) , no ponto
Ver solução completaQuestão 108
- Em cada item abaixo, calcule a derivada da função no ponto indicado.
m. e
Ver solução completaQuestão 114
Calcule as derivadas das funções abaixo (nos pontos em que elas existem):
, com
Ver solução completaQuestão 116
8 – Se a posição de um carro no instante é dada por , então a sua velocidade pode ser calculada a partir do seguinte limite
Calcule a velocidade em cada um dos casos abaixo.
a)
Ver solução completaQuestão 117
8 – Se a posição de um carro no instante é dada por , então a sua velocidade pode ser calculada a partir do seguinte limite
Calcule a velocidade em cada um dos casos abaixo.
a)
Ver solução completaQuestão 119
Usando a definição, calcule a derivada de cada uma das funções abaixo. Em seguida, determine a equação da reta tangente ao gráfico de no ponto para o valor de a indicado.
Questão 120
Usando a definição, calcule a derivada de cada uma das funções abaixo. (Veja Texto 2) Em seguida, determine a equação da reta tangente ao gráfico de f no ponto (a, f(a)), para o valor de a indicado. (Veja vídeo)
- f(x) = , a = -2
Questão 121
Usando a definição, calcule a derivada de cada uma das funções abaixo. (Veja Texto 2) Em seguida, determine a equação da reta tangente ao gráfico de f no ponto (a, f(a)), para o valor de a indicado. (Veja vídeo)
- f(x) =, a = 1
Questão 122
Usando a definição, calcule a derivada de cada uma das funções abaixo. (Veja Texto 2) Em seguida, determine a equação da reta tangente ao gráfico de f no ponto (a, f(a)), para o valor de a indicado. (Veja vídeo)
- f(x) =, a = 4
Questão 124
Q11. Determine um ponto pertencente ao gráfico de para o qual a equação da reta tangente é dada por .
Ver solução completaQuestão 126
Encontre os dois pontos onde a curva cruza o eixo x e mostre que as retas tangentes à curva nesses pontos são paralelas. Qual é o coeficiente angular comum dessas retas?
Ver solução completaQuestão 127
A Lei de Gravitação de Newton diz que a intensidade da força exercida por um corpo e massa sobre um corpo de massa é
Em que é a constante gravitacional e é a distância entre os corpos. Calcule e explique seu significado. O que o sinal de menos indica?
Ver solução completaQuestão 130
Calcule a derivada da função abaixo utilizando a definição de derivadas
Ver solução completaQuestão 131
Use a definição de derivada para encontrar as funções e seu domínio:
Ver solução completaQuestão 132
Use a definição de derivada para encontrar as funções e seu domínio:
Ver solução completaQuestão 133
Determine a equação da reta tangente a cada curva no ponto indicado:
d) em
Ver solução completaQuestão 134
Use a definição de derivada de uma função para calcular e determine a equação da reta tangente ao gráfico da função no ponto
Ver solução completaQuestão 136
Determine, se existirem, os valores de para que a função
Seja derivável em .
Ver solução completaQuestão 140
Sejam I ⊂ R um intervalo aberto e uma função. Dado , lembre que a reta tangente ao gráfico de f no ponto é a (única) reta que passa pelo ponto e tem inclinação igual a
quando o limite existe. Neste caso, a equação da reta tangente é dada por .
Para cada uma das funções abaixo, determine a inclinação em um ponto genérico. Em seguida, calcule a equação da reta tangente no ponto indicado.
(b) , no ponto
Ver solução completaQuestão 141
3 - Foi encomendado para sua empresa o projeto de um tanque para gás liquefeito de petróleo. As especificações do cliente pedem um tanque cilíndrico com extremidades hemisféricas que contenham de gás. O cliente também quer usar a menor quantidade possível de material para construir o tanque. Qual raio e altura da parte cilíndrica você recomendaria para o tanque?
Ver solução completaQuestão 143
Sejam I ⊂ R um intervalo aberto e uma função. Dado , lembre que a reta tangente ao gráfico de f no ponto é a (única) reta que passa pelo ponto e tem inclinação igual a
quando o limite existe. Neste caso, a equação da reta tangente é dada por .
Para cada uma das funções abaixo, determine a inclinação em um ponto genérico. Em seguida, calcule a equação da reta tangente no ponto indicado.
(d)
Ver solução completaQuestão 144
04) Quantas retas tangentes ao gráfico de são paralelas à reta ? Determine as equações dessas retas tangentes.
Ver solução completaQuestão 146
Seja tal que , para todo . Considere as seguintes afirmações:
- é contínua em
São verdadeiras as seguintes afirmações:
- Somente , e
- Todas
- Somente , e
- Somente e
- Somente e
Questão 147
Seja tal que , para todo . Considere as seguintes afirmações:
- é contínua em
São verdadeiras as seguintes afirmações:
- Somente , e
- Todas
- Somente , e
- Somente e
- Somente e
Questão 148
Os passos seguintes nos permitem calcular a derivada de e .
(a) Use o Limite Trigonométrico Fundamental para calcular as derivadas das funções no ponto , isto é,
,
(b) Use a identidade , os limites acima e definição de derivada para concluir que
(c) Repita o argumento acima com a identidade para concluir que .
Ver solução completaQuestão 149
Um caminhão descarrega areia a uma taxa de 3m³/min de tal forma que a areai descarregada tem um formato de cone em que a altura é igual ao diâmetro da base. Determine a taxa de crescimento da altura da pilha quando a altura for igual a 3m.
Ver solução completaQuestão 150
As montanhas da figura são modeladas pelo gráfico da função , para . Um atirador de elite, localizado na origem do sistema de coordenadas, tenta neutralizar fugitivos que escalam a montanha à direita para escapar da linha de tiro. Se os fugitivos passarem do ponto de tangência sairão do campo de visão do atirador. O problema é determinar a distância máxima entre o atirador e um alvo potencial.
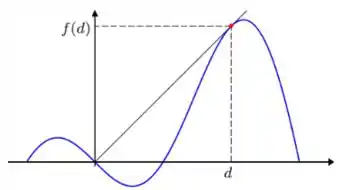
- Usando a definição, calcule .
Questão 152
As montanhas da figura são modeladas pelo gráfico da função , para . Um atirador de elite, localizado na origem do sistema de coordenadas, tenta neutralizar fugitivos que escalam a montanha à direita para escapar da linha de tiro. Se os fugitivos passarem do ponto de tangência sairão do campo de visão do atirador. O problema é determinar a distância máxima entre o atirador e um alvo potencial.
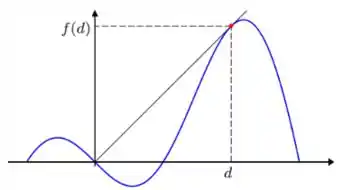
- Determine a equação da reta tangente por calculado no item acima. Em seguida, supondo que o atirador atingiu um fugitivo exatamente no ponto , calcule a distância percorrida pela bala.
Questão 153
As montanhas da figura são modeladas pelo gráfico da função , para . Um atirador de elite, localizado na origem do sistema de coordenadas, tenta neutralizar fugitivos que escalam a montanha à direita para escapar da linha de tiro. Se os fugitivos passarem do ponto de tangência sairão do campo de visão do atirador. O problema é determinar a distância máxima entre o atirador e um alvo potencial.
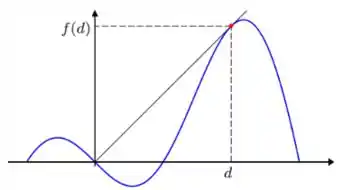
- Calcule . Em seguida, determine a equação da reta tangente ao gráfico de por um ponto genérico , com .
Questão 154
Um triângulo possui dois de seus lados iguais a 3cm e 8cm e o terceiro lado variando com o tempo. Em um certo instante, o lado mede 7cm e está aumentando a uma taxa de . Determine a taxa com a qual o ângulo oposto ao lado está variando neste momento.
Ver solução completaQuestão 155
Considere as funções e , onde são constantes reais e . Decida a veracidade das afirmações abaixo:
- Se , então é estritamente crescente
- Se , então possui exatamente um ponto de máximo e um ponto de mínimo local
- Se , então possui um único ponto crítico que não é ponto de máximo ou mínimo local
- Se , então é estritamente decrescente
- A derivada de é uma função limitada
- Se , então é estritamente crescente
- e , então possui exatamente um ponto de máximo e um ponto de mínimo local
- Se , então possui um único ponto crítico que não é ponto de máximo ou mínimo local
- Se , então é estritamente decrescente
- A derivada de é uma função limitada
Passo 1
E aí, galerinha! Tudo na paz por aí?
Vamos aqui ter que avaliar uma por uma das alternativas e usando a teoria que conhecemos, aplicar nossos conhecimentos e ver se são verdadeiras ou falsas. O enunciado não pede, mas vamos justificar todas elas pra gente ter sempre uma ideia do que estamos fazendo.
Passo 2
Falsa, pois se então . Logo, não pode ser estritamente crescente.
Verdadeira. Agora tem duas raízes, sendo negativa somente no intervalo entre essas raízes. Uma análise do crescimente da função garante o resultado.
Verdadeira. Aproveitando até o que discutimos anteriormente, a condição garante que (uma única raiz dupla) e portanto, sempre crescente, com um único ponto crítico.
Falsa, pois tem discriminante que, se negativo garante para todo , logo é estritamente crescente.
Verdadeira, pois e portanto,
Ver solução completaQuestão 156
Considere todos os triângulos retângulos cujos catetos estão contidos nos eixos coordenadas e que a hipotenusa contém o ponto (3,2). A menor área que um desses triângulos pode ter é quanto?
Ver solução completaQuestão 157
Seja uma função derivável tal que . Suponha que seja duas vezes derivável em e que . Suponha ainda que se . O valor do limite
É:
Ver solução completaQuestão 158
Seja uma função contínua derivável satisfazendo as seguintes propriedades:
- ;
- ;
Considere também que a função definida por . Decida se cada afirmação é verdadeira ou falsa:
A) A equação possui exatamente uma solução real. A solução dessa equação é um número real estritamente positivo.
B) A equação possui exatamente duas soluções reais.
C) A função possui um único ponto de mínimo local.
D) A função possui ao menos um ponto de máximo local.
E) A equação possui ao menos uma solução real.
Ver solução completaQuestão 159
Seja uma função contínua satisfazendo as seguintes propriedades:
- e
- é derivável até segunda ordem em ;
- Existe uma função contínua tal que para todo e
- Existe uma função contínua tal que para todo e
(a) Usando a Regra de L’Hospital para calcular o limite, decida se é derivável em e determine, em caso afirmativo, .
(b) Estude f em relação a seus intervalos de crescimento e decrescimento, intervalos de concavidade, pontos de máximo e mínimo locais e globais e pontos de inflexão.
(c) Esboce o gráfico de .
Ver solução completaQuestão 163
Para cada uma das seguintes funçōes, calcule pela definição a sua função derivada:
e)
Ver solução completaQuestão 167
(2) Para cada , seja . Usando a definição de derivada, prove que . [Sugestão: use o teorema binomial.]
Ver solução completaQuestão 168
(3) Usando a definição de derivada, prove que
(c) Ilustre os dois casos com o esboço de gráficos.
Ver solução completaQuestão 173
- Utilize a definição de derivada para encontrar a derivada de .
Observação: Quando se pede uma derivada sem mencionar o ponto, subentende-se que o exercício está pedindo a derivada como função, isto é, .
Ver solução completaQuestão 174
Seja f : R → R tal que e existe k ∈ R de modo que para todos e temos
Então é igual a: a. 1/6; b. 1/3; c. 1/2; d. 2/3; e. 5/6.
Ver solução completaQuestão 176
Para cada uma das seguintes funções, calcule pela definição a sua derivada:
c)
Ver solução completaQuestão 177
Para cada uma das seguintes funções, calcule pela definição a sua derivada:
e)
Ver solução completaQuestão 178
Para cada uma das seguintes funções, calcule pela definição a sua derivada:
f)
Ver solução completaQuestão 179
3 – Dada a função abaixo responda:
a) Domínio de .
b) A função inversa de .
c) Determine a derivada pela definição. (não utilizar o teorema de ).
Ver solução completaQuestão 181
Para cada uma das seguintes funçōes, calcule pela definição a sua função derivada:
i)
Ver solução completaQuestão 182
Para cada uma das seguintes funçōes, calcule pela definição a sua função derivada:
c)
Ver solução completaQuestão 183
Para cada uma das seguintes funçōes, calcule pela definição a sua função derivada:
d)
Ver solução completaQuestão 184
Para cada uma das seguintes funçōes, calcule pela definição a sua função derivada:
f)
Ver solução completaQuestão 185
Para cada uma das seguintes funçōes, calcule pela definição a sua função derivada:
g)
Ver solução completaQuestão 191
1 - Use a definição de derivada pra calcular a derivada de cada uma das funções no
ponto indicado:
d) , em .
Ver solução completaQuestão 192
1 - Use a definição de derivada pra calcular a derivada de cada uma das funções no
ponto indicado:
e) , em .
Ver solução completaQuestão 193
Para as seguintes funções calcule a derivada no ponto indicado através do limite do quociente de Newton:
Questão 195
3) Calcule, usando a definição, a derivada das seguintes funções no ponto indicado:
b)
Ver solução completaQuestão 196
3) Calcule, usando a definição, a derivada das seguintes funções no ponto indicado:
a)
Ver solução completaQuestão 198
Seja . Determinar as declividades das tangentes à elipse
em função de . Verificar que independe de . Quais são os pontos das tangentes horizontais? Quais são as tangentes (em forma cartesiana) para e ?
Ver solução completaQuestão 199
- Considere uma função com .
- Mostre que se é diferenciável num ponto então é contínua em .
- Se é contínua em então é diferenciável em ? Se sim, prove. Se não, dê um contra-exemplo.
Ver solução completaQuestão 200
9. Determine a derivada da função em cada caso.
a) Utilizando a definição de derivada.
b) Utilizando regras de derivação.
Ver solução completaQuestão 202
Um ponto desloca-se sobre o gráfico da curva . No instante em que ele se encontra no ponto (2,), a taxa de variação de sua abscissa é 10m/s. A taxa de variação da distância do ponto até a origem neste mesmo instante é
a. ; b. ; c. ; d. ; e. −.
Ver solução completaQuestão 203
Sejam cujos gráficos são:
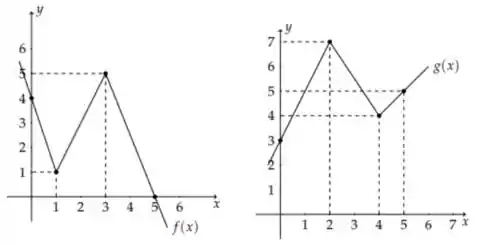
Sejam dadas por e . O valor é:
a) ;
b) ;
c) ;
d) ;
e) .
Ver solução completaQuestão 204
Até mesmo os grandes gênios da humanidade às vezes se equivocam. No início dos
seus estudos sobre os corpos em queda, em uma carta2 a P. Sarpi em 16 de outubro de
1604, Galileo escreveu “[...] gli spazzii passati dal moto naturale esser in proporzione
doppia dei tempi [...] il mobile naturale vadia crescendo di velocit`a con quella proportione
che si discosta dal principio del suo moto [...]”.
- Prove que Galileo se equivocou: se um corpo cai uma distância em t segundos, e s’ é proporcional a s, então s não pode ser uma função da forma .
Questão 205
Até mesmo os grandes gênios da humanidade às vezes se equivocam. No início dos
seus estudos sobre os corpos em queda, em uma carta2 a P. Sarpi em 16 de outubro de
1604, Galileo escreveu “[...] gli spazzii passati dal moto naturale esser in proporzione
doppia dei tempi [...] il mobile naturale vadia crescendo di velocit`a con quella proportione
che si discosta dal principio del suo moto [...]”.
b) Mostre que os seguintes fatos são verdadeiros a respeito de s se : (i)s′′(t) = a (a aceleração é constante); (ii) .
Ver solução completaQuestão 206
(a) Suponha que (i) , (ii) para todo x, e (iii). Prove que g é diferenciavel em a e que .
Ver solução completaQuestão 208
Determine a equação da reta tangente às seguintes curvas, nos pontos indicados. Esboce o gráfico em cada caso:
(a)
Ver solução completaQuestão 209
Para cada uma das seguintes funções, calcule pela definição a sua derivada:
a)
Ver solução completaQuestão 210
Para cada uma das seguintes funções, calcule pela definição a sua derivada:
b)
Ver solução completaQuestão 211
Para cada uma das seguintes funções, calcule pela definição a sua derivada:
d)
Ver solução completaQuestão 212
Para cada uma das seguintes funções, calcule pela definição a sua derivada:
g)
Ver solução completaQuestão 213
Para cada uma das seguintes funções, calcule pela definição a sua derivada:
h)
Ver solução completaQuestão 214
Para cada uma das seguintes funções, calcule pela definição a sua derivada:
i)
Ver solução completaQuestão 223
(3) Usando a definição de derivada, prove que
(a) se , onde é uma constante, então .
Ver solução completaQuestão 229
As montanhas da figura são modeladas pelo gráfico da função , para . Um atirador de elite, localizado na origem do sistema de coordenadas, tenta neutralizar fugitivos que escalam a montanha à direita para escapar da linha de tiro. Se os fugitivos passarem do ponto de tangência sairão do campo de visão do atirador. O problema é determinar a distância máxima entre o atirador e um alvo potencial.
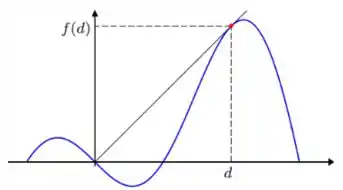
- Determine o valor de , sabendo que a reta tangente à montanha por passa pela origem e que .
Questão 230
Em cada um dos itens abaixo, encontre a derivada da função usando a definição:
d)
Ver solução completa