Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 4.2 - Ex. 3
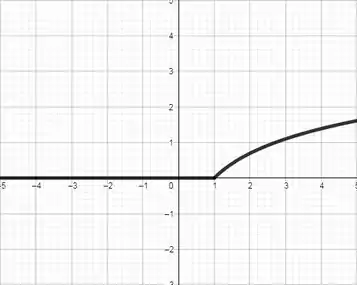
1-10. Esboce o gráfico de onde
3.
Passo 1
Como a função é definida por partes, a integral também será, por isso devemos analisar cada expressão que essa integral pode assumir dependendo dos casos (os casos são definidos pelas restrições em que ditam a lei a função ).
Caso 1:
Nesse caso, temos que
Caso 3:
Nesse caso, temos que
Desta forma, nossa função será definida por:
Calculando as integrais de cada parte da função temos:
Agora basta esboçar cada parte de , em um único gráfico. A primeira parte define um reta horizontal e a segunda parte define uma curva logarítmica.
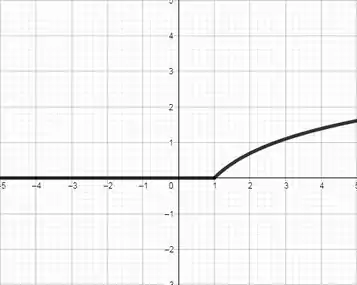
Resposta
Exercícios de Livros Relacionados
Resolver as seguintes integrais usando a técnica de integração por partes. ∫ ln ( 1 - x ) d x
Resolver as seguintes integrais usando a técnica de integração por partes. ∫ e a x s e nb xd x
Resolver as seguintes integrais usando a técnica de integração por partes. ∫ x 2 e x d x
Resolver as seguintes integrais usando a técnica de integração por partes. ∫ x 2 ln x d x
Resolver as seguintes integrais usando a técnica de integração por partes. ∫ ( x - 1 ) e - x d x