Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.9 - Ex. 18
18- Use um sistema algébrico computacional para plotar o campo vetorial
no cubo obtido cortando o primeiro octante pelos planos , e . Em seguida calcule o fluxo através da superfície do cubo.
Passo 1
Faala, pessoal!
Essa questão pede duas coisas.
A primeira é plotar o campo vetorial num cubo. Pra isso, vamos usar o software Mathematica.
A segunda é calcular o fluxo desse campo na superfície do cubo. Pra isso, aplicamos o teorema do divergente, que diz:
Onde é o sólido limitado pela superfície , e o divergente de é
Então vamos calcular esse divergente, definir quem é , e calcular a integral tripla!
Passo 2
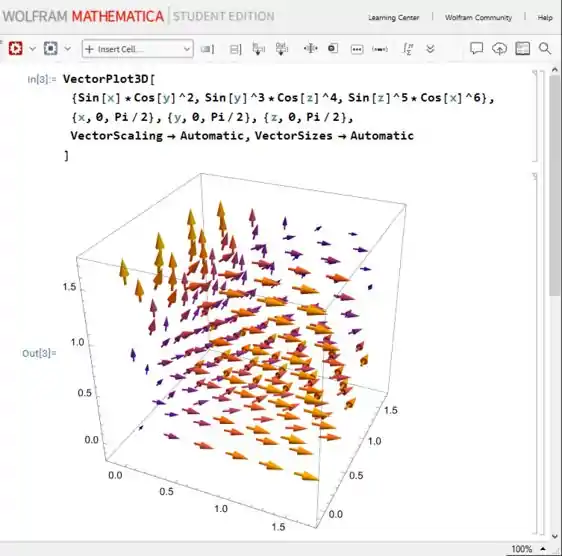
Começando com o desenho do campo:
Como nosso cubo está no primeiro octante,
E está sendo limitado pelos planos
Então:
Vamos usar o comando “VectorPlot3D” no Mathematica, pra plotar o campo vetorial nesses intervalos (que definem o cubo), só que pra melhorar o visual, vou incluir mais dois comandos:
VectorScaling Automatic
VectorSizes Automatic
Esses dois atributos, dentro do comando “VectorPlot” deixam o ajuste de tamanho e escala dos vetores automáticos, o que facilita a nossa visualização do campo. Então, o comando e a resposta ficam assim:
Passo 3
Agora vamos calcular o divergente de , onde:
Derivando em função de , com constantes:
E derivando em função de , vamos ter que usar a regra da cadeia:
Por último, derivando em função de , de novo com a regra da cadeia:
E o divergente fica:
Passo 4
Pra chegar da integral, só falta definirmos quem é o .
Bom, se a superfície é a superfície do cubo, o sólido vai ser o próprio cubo definido por:
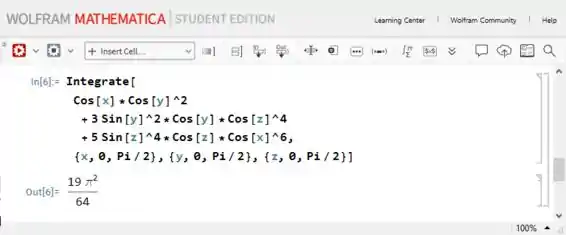
Então a integral fica:
Passo 5
Jogando no Mathematica, encontramos o resultado:
Resposta
